 |
Operations
Research (MTH601)
259
Segment IX:
Dynamic
Programming
Lectures
42- 43
INTRODUCTION
Dynamic
programming is basically a mathematical
technique developed by Richard
Bellman and his
associates
at the Rand Corporation. This
technique is a powerful tool
for making a sequence of
interrelated
decisions.
There is no standard mathematical
formulation of the dynamic programming
problem, which is in
259
Operations
Research (MTH601)
260
contrast
to linear programming. It is a general
type of approach to problem solving
and each problem has
to
be
analyzed depending on the
conditions pertaining to the
problem and the particular
equations used must
be
developed
to suit the problem. In this
way one should take
care to formulate a dynamic programming
problem,
using
the method of
recursion.
Dynamic
programming provides a solution with
much less effort than
exhaustive enumeration. In
dynamic
programming we start with a
small portion of the problem
and find the optimal
solution for this
smaller
problem.
We then gradually enlarge
the problem finding the
current optimal solution from
the previous one,
until
we solve the original problem in its
entirety. In this connection we refer to Bellman's
principle of
optimality,
which states:
"An
optimal policy has the
property that, whatever the
initial state and initial
decision are, the
remaining
decisions must constitute an
optimal policy with respect
to the state resulting from
the first decision".
Dynamic
programming technique can be
applied to problems of inventory control,
production
planning,
chemical reactor design,
heat exchanger designs,
business situation to take an
optimal decision for
investments
etc.
A
number of illustrative examples
are presented for developing
dynamic programming procedure.
We
consider the following
problem called "Stage coach
problem" to illustrate the concepts
of
Example
dynamic
programming. A salesman has to
travel between points A to B
indicated by the network shown
in
figure
2
5
8
1
3
6
9
A
B
7
4
The
distance to be traveled by the
salesman from various states
to other states, is given
below.
2
3
4
5
6
7
8
9
10
1
20 40 30
2
70 40 60
5
10 40
8
30
3
30 20 40
6
60 30
9
40
4
40 10 50
7
30 30
Which
route minimizes the total
distance traveled from A to
B.
Solution:
260
Operations
Research (MTH601)
261
First
point we note in this problem is
that the decision, which is
best for each successive
stage, need
not
yield the over-all optimal
decision.
If
we follow the policy of
minimum distance at each
state, we land in a path A→2→6→9→B,
with a
total
distance travelled as 130
km. However it should be
evident that sacrificing a little on
one is less distant
that
A→2→6
= (2 + 4).
We
can solve the problem by
trial and error. The
number of possible routes is 18 in this
example and
having
to calculate the total distance
for all routes is a tiresome
task. Instead of exhaustive
enumeration of all
the
routes, it is better to start
with a small problem and
find the optimal solution
for this smaller problem.
Thus
we
extend this for the
entire problem. This is what we try to do
in dynamic programming.
The
problem is divided into a number of
stages and proceeds
backwards from final
destination. In this
example
if we were in 8 or 9 and the
final destination is B we have to
travel only one stage to
complete the
journey.
This we call as one stage
problem indicating that there is
one more stage to go to
complete the journey.
If
we were in 5 or 6 or 7 we have to travel
2 stages to reach the final
destination. Like this we have 4
stages from
A
to B.
Let
xn(n
= 1, 2, 3, 4) be the immediate destination
when there are
n
more
stages to travel. Thus,
the
route
selected would be 1→x4→x3→x2→x1,
where x1
= 10. Let
fn(x, xn) be the total
cost of the best
over-all
policy
for the last n
stages,
given that the salesman is
in the state s
and
selects xn as
the immediate destination
called
the state. Given s
and
n,
let xn*
denote the value of xn which minimizes fn(s1, xn), and let fn*(s)
be the
corresponding
minimum value of fn(x,
xn). Thus, fn*(s) = fn(s, xn*). The
objective is to find f4*(1) and
the
corresponding
policy. In dynamic programming we
successively find f1*(s),
f2*(s), f3*(s) and
f4*(1).
The
problem is divided into four stages. In
one stage problem, we have
one more stage to go, we
can
write
the solution to one-stage problem as
follows.
s
f1*(s)
x1*
8
30
10
9
40
10
When
the salesman has two
more stages to go, the
solution requires a little analysis.
When two stages are
ahead
to
reach final destination he may
occupy one of the states 5
or 6 or 7. If he is in state 5, he must go to
either state
8
or 9 at a cost of 10 or 40 respectively. If he
selects state 8, the minimum
additional distanced to travel
after
reaching
there, is given in the above
table as 30 so that the total
distance for this decision
would be 10 + 30 =
40.
If he selects state 9, the total
distance is 40 + 40 = 80. Comparing
the two cases, it is better
if he would
choose
8, x2*
= 8, since it gives the
minimum total distance, f2*(5) = 40. In the
same way for s = 6 and s =
7, we
get
the following results for
the two stage problem
shown below.
x2
f2(s, x2) =
Cs x2
+
f1*(x2)
f2*(s) x2*
s
8
9
5
10
+ 30 = 40
40
+ 40 = 80
40
8
6
60
+ 30 = 90
30
+ 40 = 70
70
9
7
30
+ 30 = 60
30
+ 40 = 70
60
8
The
solution for the three-stage
problem is obtained in a similar
fashion. In the three-stage
problem, we
have
f3(s,
x3) = Csx3 +
f2*(x3). To illustrate, if the
salesman is in state 2, and
selects to go to state 5 next,
the
minimum
total distance, f3(2,
5) would be the cost of the
first stage C25
= 70 plus
the minimum distance
from
state
5 onward f2*(5)
= 4 so that f3*(2, 5) = 70 + 40 = 110,
similarly f5*(2, 6) = 40 + 70 = 110
and f3*(2, 7) = 60
261
Operations
Research (MTH601)
262
+
60 = 120, so that the
minimum total distance from
state 2 onward is f3*(2)
= 110 and the
immediate
destination
should be x3*
= 5 or 6. The results are
tabulated below.
x3
f3(s, x3) =
Csx3 +
f2*(x3)
f3*(s) x3*
s
5
6
7
2
70
+ 40 = 110 40 + 70 = 110 60 + 60 =
120
110
5 or 6
3
30
+ 40 = 70 20 + 70 = 90 40 + 60 =
120
70
5
4
40
+ 40 = 80 10 + 70 = 80 50 + 60 =
110
80
5 or 6
Continuing
in this way, we move to the
four-stage problem. The
optimum distance travelled
given the
immediate
destination, is again the
sum of the distances of the
first stage plus the
minimum distance
thereafter.
The
results are tabulated in
table.
x4
f4(s, x4)
=
C
sx4 + f3*(x4)
s
2
3
4
f4*
(x) x4*
1
20
+ 110 = 130
40
+ 70 = 110 30 + 80 = 110
110
3 or 4
We
can summarize the optimal
solution. From the four stage
problem, we infer that the
salesman
should
go initially to either state 3 or
state 4. If he chooses x4*
= 3, the three-stage problem
result for s = 3 is x4*
=
5. From this we go to the two
stage problem which gives
x*2 = 8 for s = 5 and the
single stage problem
yields
x1* = 10
for s = 8. Hence the optimal
route is 1→3→5→8→10.
If the salesman selects x4*=4, this leads to
the
other
two optimal routes, 1→4→5→8→10
and 1→4→6→9→10.
They all yield a total of
f4*(1)
= 110.
FEATURES
CHARECTERIZING DYNAMIC PROGRAMMING
PROBLEMS
The
physical interpretation to the
abstract structure of dynamic programming
problems can be
provided
by
the example of stagecoach
problem discussed in the
previous section. Any
problem in dynamic programming
can
be formulated with its basic
structure similar to that of
the stagecoach problem. The
basic features, which
characterize
dynamic programming problems, are
given in the
following.
1.
The
problem can be divided up into
stages, with a policy
decision required at each
stage.
2.
Each
stage has a number of states
associated with it.
3.
The
effect of the policy
decision at each stage is to
change the current state
into a state associated
with
the
next stage.
4.
Given
the current state, an
optimal policy for the
remaining stage, is independent of
the policy adopted
in
previous stages.
5.
The
procedure of solving the problem
begins by finding the
optimal policy for each
state of the last
stage.
6.
A
recursive formula can be framed to
identify the optimal policy
for each state with
(n
-
1) stages
remaining.
7.
Using
the recursive relationship
the procedure is to move
backward stage by stage,
until it finds the
optimal
policy when starting at the
initial stage.
Six
units of capital is available to
invest in four business ventures.
The returns from each
unit
Example
of
investment in all the four
ventures are given in the
table below. Find how
should the capital be
allocated to
business
proposals in order to maximize
profit.
262
Operations
Research (MTH601)
263
Expected
returns from
Business
proposals
Unit
A
B
C
D
0
0
0
0
0
1
5
2
6
2
2
6
4
7
3
3
7
6
8
4
4
8
8
8
5
5
8
9
8
6
6
8
10
8
6
The
problem has 4 stages, each
business proposal representing a
stage and we have six
states
Solution:
with
each stage.
One
stage problem
Here
we consider only one
business proposal namely D
(working backward) we can
allot any unit of
capital
and the expected returns
are as shown in table. For
business D alone,
S
f1*(s)
x1*
0
0
0
1
2
1
2
3
2
3
4
3
4
5
4
5
6
5
6
6
5,6
Two-stage
problem:
Here
we consider two business
proposals D and C. The
capital is to be allocated to D and C in
many
possible
ways. If a certain unit of capital is
allotted to C (second new business)
then the remaining capital
only
can
be allocated to D and we have
several combinations. The
convenient way to understand
about the returns is
to
analyse all possible
combinations. Let x1,
be the amount allotted to D
and x2
to C.
263
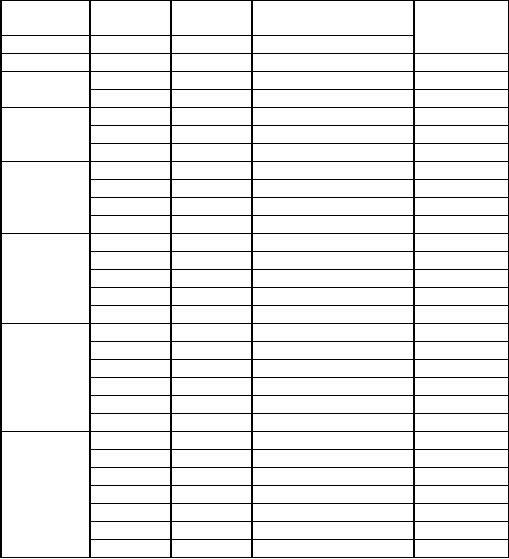
Operations
Research (MTH601)
264
Then
profit function;
f2 (s, x2) = p(x2) +
f1*(s, x2).
Capital,
s,
Allotment
Allotment
Net
Return from
x2*
for
C
for
D
two
ventures
s
= x2 +
x1
x2
x1
f2(s)
s=0
0
0
0
s=1
0
1
0+2=2
1
0
6
+ 0 = 6*
1
s=2
0
2
0+3=3
1
1
6
+ 2= 8*
1
2
0
7+0=7
s=3
0
3
0+4=7
1
2
6
+ 3 = 9*
1
2
1
7
+ 2 = 9*
1,
2
3
0
8+0=8
s=4
0
4
0+5=5
1
3
6
+ 4 = 10 *
1
2
2
7
+ 3 = 10 *
1,
2
3
1
8
+ 2 = 10 *
1,
2, 3
4
0
8+0=8
s=5
0
5
0+6=6
1
4
6
+ 5 = 11*
1
2
3
7
+ 4 = 11*
1,2
3
2
8
+ 3 = 11*
1,
2,3
4
1
8
+ 2 = 10
5
0
8+0=8
s=6
0
6
0+6=6
1
5
6
+ 6 = 12*
1
2
4
7
+ 5 = 12*
1,
2
3
3
8
+ 4 = 12*
1,
2, 3
4
2
8
+ 3 = 11
5
1
8
+ 2 = 10
6
0
8+2=8
Now
we turn to a three-stage problem.
Here we consider three
business ventures. The
capital can be
allotted
to business venture B (= x3)
and the remaining amount to
C and D combined.
264
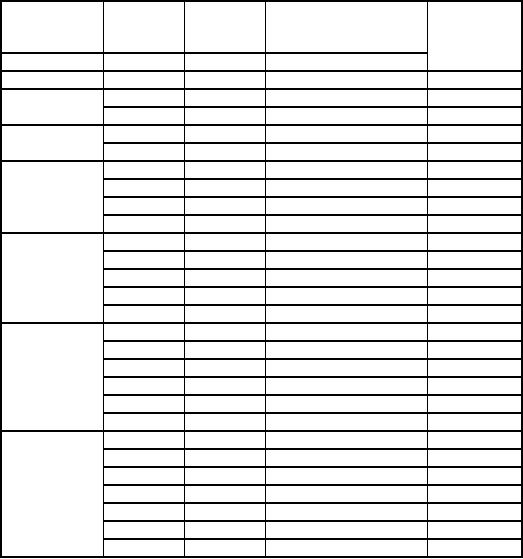
Operations
Research (MTH601)
265
The
profit function is given by
f3(s, x3) = p(x3) +
f2*(s-x3)
Capital,
s,
Allotment
Allotment
Net
Return from
x3*
for
B
for
C and
three
ventures
D
s
= x3 +
(s-x1)
(x3)
(s-x3)
f3(s)
s=0
0
0
0
s=1
0
1
0
+ 6 = 6*
0
1
0
2+0=2
s=2
0
2
2
+ 6 = 8*
0
1
1
4+0=4
0,
1
s=3
0
3
0+9=9
1
2
2
+ 8 = 10*
1
2
1
4
+ 6 = 10*
1,
2
3
0
6+0=6
s=4
0
4
0
+ 10 = 10
1
3
2
+ 9 = 11
2
2
4
+ 8 = 12 *
2
3
1
6
+ 6 = 12 *
2,
3
4
0
8+0=8
s=5
0
5
0
+ 11 = 11
1
4
2
+ 10 = 12
2
3
4
+ 9 = 13
3
2
6
+ 8 = 14*
3
4
1
8
+ 6 = 14*
3,4
5
0
9+0=9
s=6
0
6
0
+ 12 = 12
1
5
2
+ 11 = 13
2
4
4
+ 10 = 12*
3
3
6
+ 9 = 15
4
2
8
+ 8 = 16*
4
5
1
9
+ 6 = 15
6
0
10
+ 0 = 10
Now
finally, we come to the
four-stage problem, in which we
consider all the business
proposals A, B, C and D.
A
certain capital is allotted to A
and the remaining for B, C
and D together for which
the optimum result can
be
taken
from the three-stage
problem.
265
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION