ZeePedia

Simplification of Boolean Expression, Standard POS form, Minterms and Maxterms

<< Boolean Addition, Multiplication, Commutative Law, Associative Law, Distributive Law, Demorgan’s Theorems
KARNAUGH MAP, Mapping a non-standard SOP Expression >>
img
CS302 - Digital Logic & Design
Lesson No. 09
BOOLEAN ALGEBRA AND LOGIC SIMPLIFICATION
Boolean Analysis of Logic Circuits, evaluating of Boolean expressions, representing
the operation of Logic circuits and Boolean expressions in terms of Function tables and
representing Boolean expressions in SOP and POS forms are inter-related. Boolean laws,
rules and theorems are used to readily change from one form of representation to the other.
Two examples are considered which illustrate the analysis, simplification and
representation of Logic Circuits and Boolean expressions. In both the examples, a Boolean
expression representing the Logic Circuit is developed, the Boolean expression is evaluated
and a function table is implemented that represents the Boolean expression and the function
of the Logic Circuit. Each Boolean expression is also simplified into SOP or POS form, the
simplified expression is presented in a function table format. The original and the simplified
expressions are verified to show identical functions.
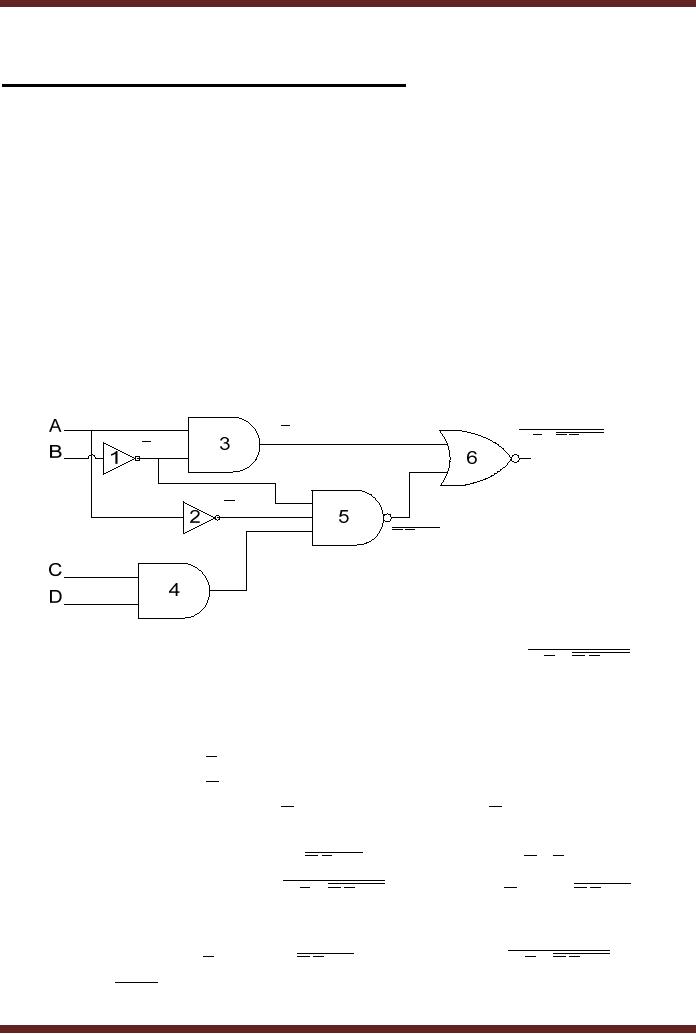
Example 1
1. Finding the Boolean Expression
A.B
A.B + A.B.C.D
B
A
A.B.C.D
C.D
Logic Circuit represented by Boolean expression A.B + A.B.C.D
Figure 9.1
The circuit can be represented by a Boolean Expression. Starting from the left hand
side
·  Output of NOT gate 1 is B
·  Output of NOT gate 2 is A
·  Output of two input AND gate 3 is A.B
(product of A and B
·  Output of two input AND gate 4 is C.D
(product of C and D)
·
Output of three input NAND gate 5 is A.B.C.D
NOT(product of A , B and CD)
Output of two input NOR gate 6 is A.B + A.B.C.D
·
NOT(sum of A.B and A.B.C.D )
2. Evaluating the Expression
and Y = A.B.C.D .
expression A.B + A.B.C.D
X = A.B
The
can
be
Considering
that
represented by X + Y .
79
img
CS302 - Digital Logic & Design
The output of the logic circuit is 1 when X = 0 and Y = 0
·  X=0 NOR Y=0 Output = 1
·  X=0 NOR Y=1 Output = 0
·  X=1 NOR Y=0 Output = 0
·  X=1 NOR Y=1 Output = 0
X= A.B = 0 when any literal is zero. That is, A =0 or B =0 (B=1)
Y= A.B.C.D = 0 when A.B.C.D = 1
A.B.C.D = 1 when all literals are one. That is A =1 (A=0), B =1 (B=0), C=1 and D=1
The expression output is 1 for the input conditions
(A=0 OR B=1) AND (A=0 AND B=0 AND C=1 AND D=1)
That is, A=0, B=0, C=1and D=1.
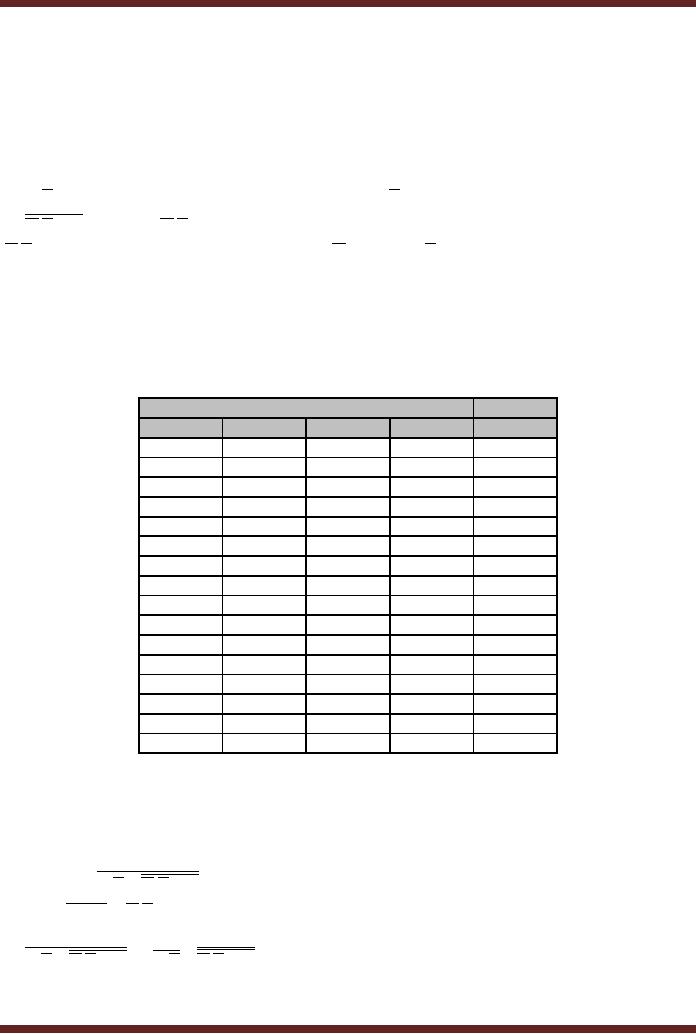
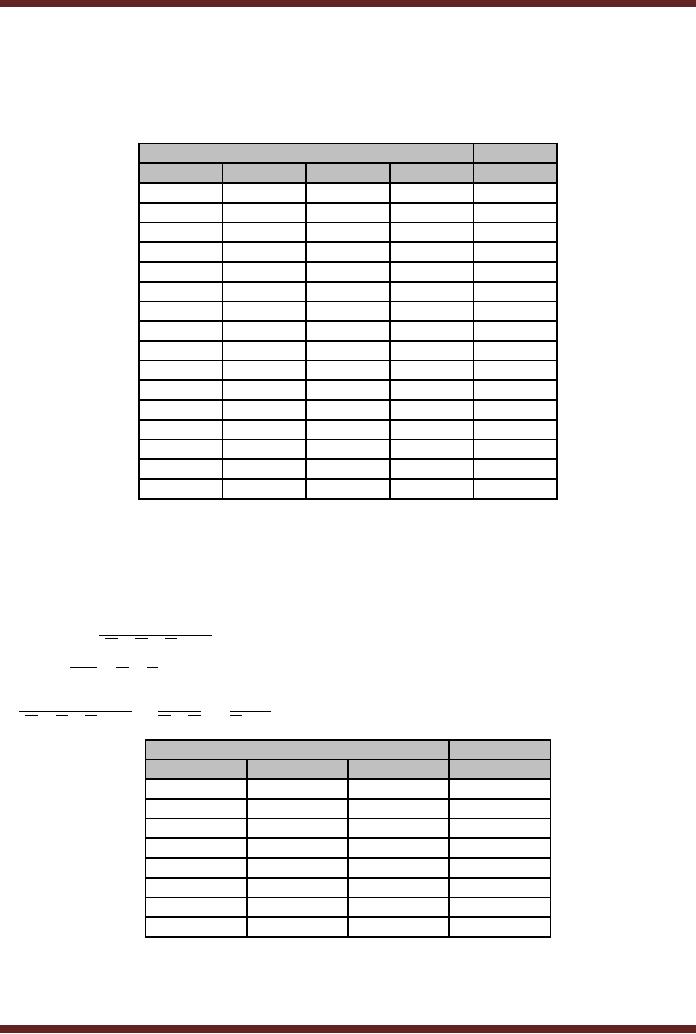
3. Putting the Results in Truth Table Format
Input
Output
A
B
C
D
F
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
0
1
1
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
Table 9.1
Truth Table representing function of Logic Circuit (fig. 9.1)
4. Simplification of Boolean Expression
The A.B + A.B.C.D expression can be simplified by applying Demorgan's second
theorem A + B = A.B .
= ( A.B + A.B.C.D = (A.B).(A.B.C.D)
Apply Demorgan's first theorem to the first term and Rule 9 to the second term
80
img
CS302 - Digital Logic & Design
= (A + B).(A.B.C.D)
= (A + B).(A.B.C.D)
Using the Distributive Law
= (A.A.B.C.D) + A.B.B.C.D
Applying Rule 8 to the second term
= A.B.C.D
expression =1 when all literals are one
that is A =1 AND B =1 AND C=1 AND D=1
or A=0 AND B=0 AND C=1 AND D=1
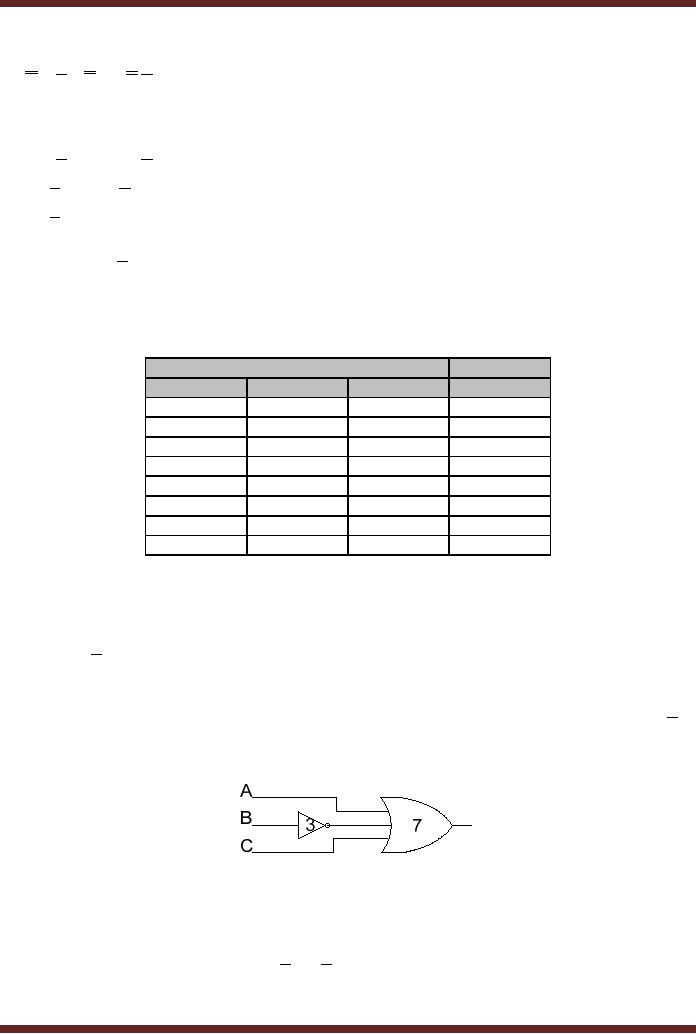
5. Putting the result in Truth Table format
Input
Output
A
B
C
D
F
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
0
1
1
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
0
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
Table 9.2
Truth Table representing function of simplified expression
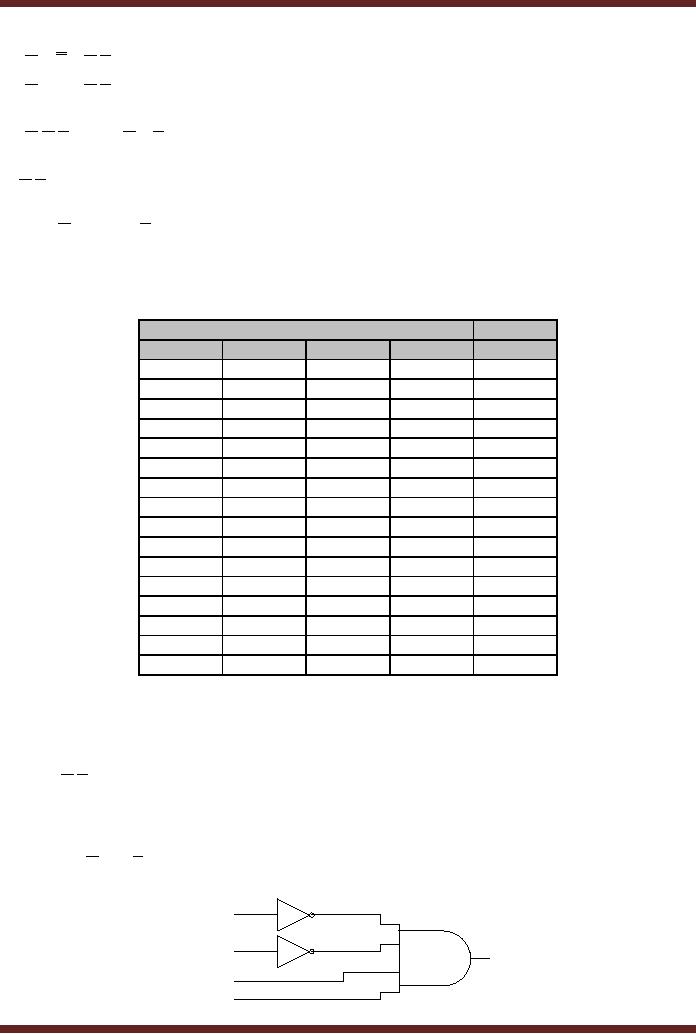
6. Implementing Logic Circuit from Simplified Boolean expression
F = A.B.C.D
The expression F represents a product term having four literals. Product term is implemented
using AND gates. Since, the product has four literals therefore a 4-input AND gate is used.
The literals A and B are implemented using NOT gates.
A
3
B
4
7
C
D
81
img
CS302 - Digital Logic & Design
Figure 9.2
Simplified Logic Circuit
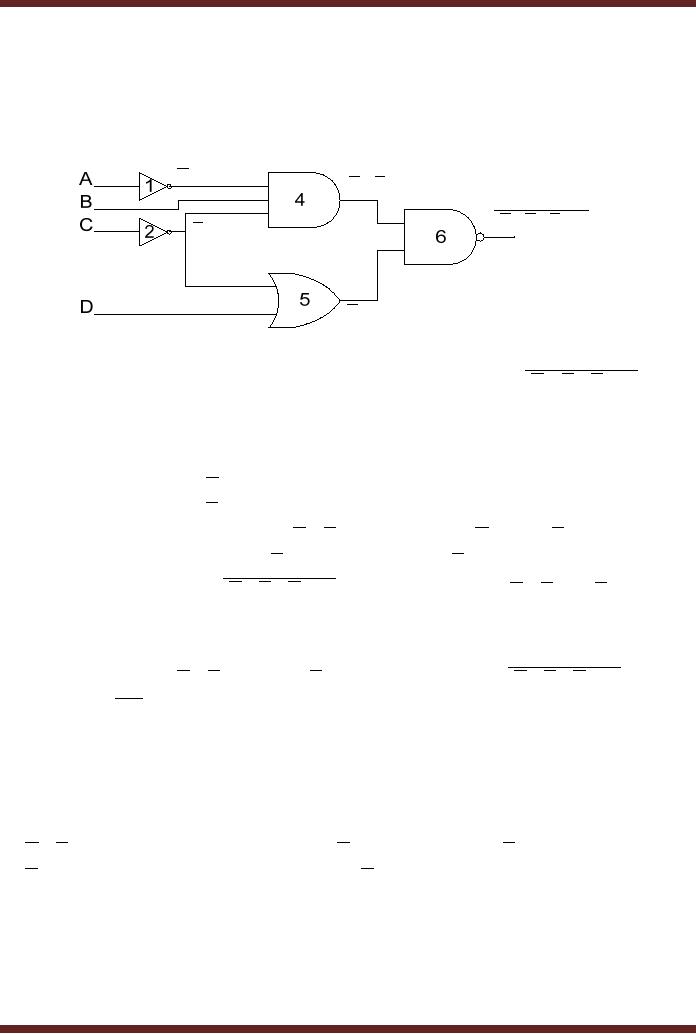
Example 2
1. Finding the Boolean Expression
A
A.B.C
(A.B.C).(C + D)
C
C+D
Logic Circuit represented by Boolean expression (A.B.C).(C + D)
Figure 9.3
The circuit can be represented by a Boolean Expression. Starting from the left hand
side
·  Output of NOT gate 1 is A
·  Output of NOT gate 2 is C
·
Output of three input AND gate 4 is A.B.C
(product of A , B and C )
Output of two input OR gate 5 is C + D
·
(sum of C and D)
Output of NAND gate 6 is (A.B.C).(C + D)
NOT(product of A.B.C and C + D )
·
2. Evaluating the Expression
Considering that X = A.B.C and Y = C + D . The expression (A.B.C).(C + D) can be
represented by X.Y .
The output of the logic circuit is 1 when X=0 or Y=0
·  X=0 NAND Y=0 Output = 1
·  X=0 NAND Y=1 Output = 1
·  X=1 NAND Y=0 Output = 1
·  X=1 NAND Y=1 Output = 0
X= A.B.C = 0 when any literal is zero. That is, A =0 (A=1) or B =0 or C =0 (C=1)
Y= C + D = 0 when both literals are zero. That is C =0 (C=1) and D=0
The expression output is 1 for the input conditions
(A=1 OR B=0 OR C=1) OR (C=1 AND D=0)
82
img
CS302 - Digital Logic & Design
3. Putting the Results in Truth Table Format
Input
Output
A
B
C
D
F
0
0
0
1
0
0
0
1
1
0
0
1
0
1
0
0
1
1
0
1
0
1
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
0
1
1
0
1
0
1
1
1
0
1
1
0
0
1
1
1
0
1
1
1
1
1
1
1
0
1
1
1
1
1
Table 9.2
Truth Table representing function of Logic Circuit (fig. 9.3)
The truth table shows that the variable D has no effect on the output of the circuit. The truth
table reduces to a three variable truth table. Table 9.3
4. Simplification of Boolean Expression
The (A.B.C).(C + D) expression can be simplified by applying Demorgan's first
theorem A.B = A + B .
= (A.B.C).(C + D) = (A.B.C) + (C + D)
Input
Output
A
B
C
F
0
0
0
1
0
0
1
1
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
1
Table 9.3
Alternate Truth Table representing function of Logic Circuit (fig. 9.3)
Apply Demorgan's first and second theorems to the first and second terms respectively
83
img
CS302 - Digital Logic & Design
= (A + B + C) + (C.D)
Applying Rule 9
= (A + B + C) + (C.D)
= A + B + C(1 + D)
= A +B+C
expression =1 when any one literal is one
that is A=1 OR B =1 OR C=1
or A=1 OR B=0 OR C=1
5. Putting the result in Truth Table format
Input
Output
A
B
C
F
0
0
1
0
0
1
0
1
0
1
0
0
0
1
1
1
0
1
1
0
1
1
0
1
1
0
1
1
1
1
1
1
Table 9.4
Truth Table representing function of simplified expression
6. Implementing Logic Circuit from Simplified Boolean expression
F = A +B+C
The expression F represents a sum term having three literals. Sum term is implemented using
OR gates. Since, the sum has three literals therefore a 3-input OR gate is used. The literal B is
implemented using NOT gate.
Figure 9.4
Simplified Logic Circuit
Standard SOP form
A standard SOP form has product terms that have all the variables in the domain of the
expression. The SOP expression AC + BC is not a standard SOP as the domain of the
expression has variables A, B and C.
84
img
CS302 - Digital Logic & Design
A non-standard SOP is converted into a standard SOP by using the rule A + A = 1
AC + BC
= AC(B + B) + (A + A)BC
= ABC + ABC + ABC + ABC
= ABC + ABC + ABC
Standard POS form
A standard POS form has sum terms that have all the variables in the domain of the
expression. The POS expression (A + B + C)(A + B + D)(A + B + C + D) is not a standard
POS as the domain of the expression has variables A, B, C and D.
A non-standard POS is converted into a standard POS by using the rule AA = 0
(A + B + C)(A + B + D)(A + B + C + D)
= (A + B + C + D)(A + B + C + D)(A + B + C + D)(A + B + C + D)(A + B + C + D)
Converting to Standard SOP and POS forms
There are several reasons for converting SOP and POS forms into standard SOP and
POS forms respectively.
Any logic circuit can be implemented by using either the SOP, AND-OR combination of
gates or POS, OR-AND combination of gates. It is very simple to convert from standard SOP
to standard POS or vice versa. This helps in selecting an implementation that requires the
minimum number of gates. Secondly, the simplification of general Boolean expression by
applying the laws, rules and theorems does not always result in the simplest form as the ability
to apply all the rules depends on ones experience and knowledge of all the rules.
A simpler mapping method uses Karnaugh maps to simplify general expressions.
Mapping of all the terms in a SOP form expression and the sum terms in a POS form can be
easily done if standard forms of SOP and POS expressions are used. Karnaugh maps will be
discussed latter in the chapter.
Lastly, the PLDs are implemented having a general purpose structure based on AND-
OR arrays. A function represented by an expression in Standard SOP form can be readily
programmed.
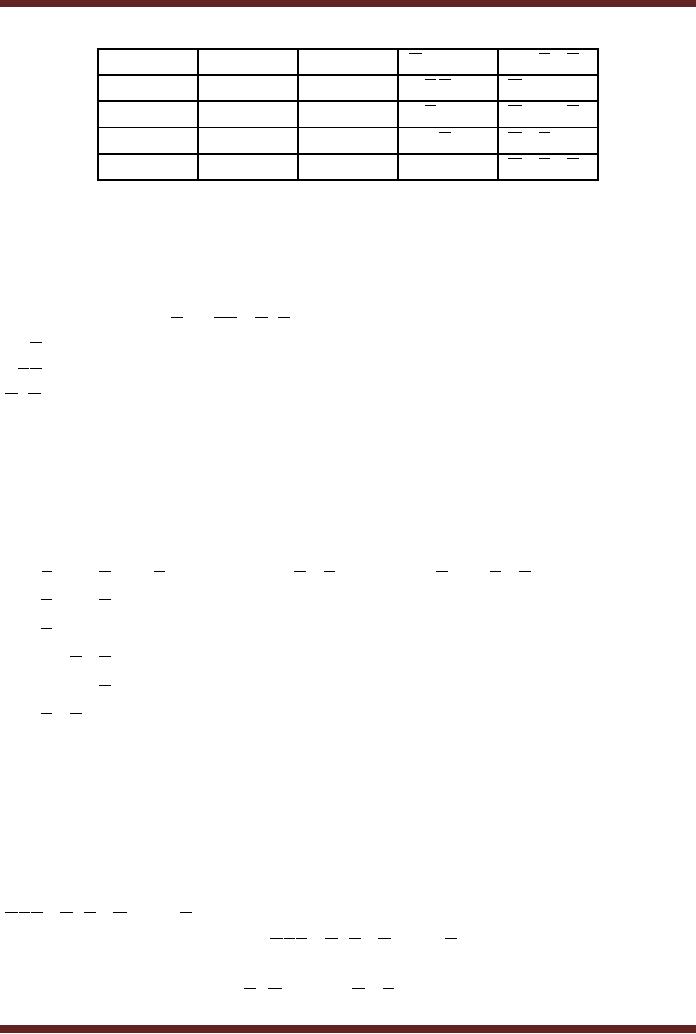
Minterms and Maxterms
The Product terms in the Standard SOP form are known as Minterms and the Sum
terms in the Standard POS form are known as Maxterms.
A
B
C
Minterms
Maxterms
A +B+C
0
0
0
A.B.C
0
0
1
A +B+C
A.B.C
0
1
0
A +B+C
A.B.C
85
img
CS302 - Digital Logic & Design
0
1
1
A +B+C
A.B.C
1
0
0
A +B+C
A.B.C
1
0
1
A +B+C
A.B.C
1
1
0
A +B+C
A.B.C
A.B.C
1
1
1
A +B+C
Table 9.5
Table of Minterms and Maxterms
Binary representation of a standard Product term or Minterm
A standard product term is equal to one for only one combination of variable values.
For all other variable values the standard product term is equal to zero.
For the expression ABC + ABC + ABC
ABC =1
if A=1, B=1 and C=0
ABC =1
if A=1, B=0 and C=0
ABC =1
if A=0, B=1 and C=0
An SOP expression is equal to 1 when one or more product terms in the expression are equal
to 1.
Binary representation of a standard Sum term or Maxterm
A standard sum term is equal to zero for only one combination of variable values. For
all other variable values the standard sum term is equal to one.
For the expression
(A + B + C + D)(A + B + C + D)(A + B + C + D)(A + B + C + D)(A + B + C + D)
(A + B + C + D) =0
if A=0, B=1, C=0 and D=1
(A + B + C + D) =0
if A=0, B=1, C=0 and D=0
(A + B + C + D) =0
if A=0, B=0, C=1 and D=1
(A + B + C + D) =0
if A=0, B=0, C=0 and D=1
(A + B + C + D) =0
if A=0, B=1, C=1 and D=0
A POS expression is equal to 0 when one or more product terms in the expression are equal
to 0.
Converting Standard SOP into Standard POS
The binary values of the product terms in a given standard SOP expression are not
present in the equivalent standard POS expression. Also, the binary values that are not
represented in the SOP expression are present in the equivalent POS expression.
ABC + ABC + ABC + ABC + ABC has the binary values 000, 010,011,101 and 111
Canonical Sum = ∑  A,B,C (0,2,3,5,7) = ABC + ABC + ABC + ABC + ABC
The missing binary values are 001, 100 and 110.
The POS expression is (A + B + C)(A + B + C)(A + B + C)
86
img
CS302 - Digital Logic & Design
Canonical Product = ∏  A,B,C (1,4,6)
Verifying POS expression is equivalent to SOP expression
(A + B + C)(A + B + C)(A + B + C)
= (A.A + A.B + A.C + A.B + B.B + B.C + A.C + B.C + C.C).(A + B + C)
= (A.B + A.C + A.B + B + B.C + A.C + B.C).(A + B + C)
= (A.C + B + A.C).(A + B + C)
= A.A.C + A.B.C + A.C.C + A.B + B.B + B.C + A.A.C + A.B.C + A.C.C
= A.B.C + A.C + A.B + B.C + A.C + A.B.C
Converting into standard SOP
= A.B.C + A.C(B + B) + A.B(C + C) + B.C(A + A) + A.C(B + B) + A.B.C
= A.B.C + A.B.C + A.B.C + A.B.C + A.B.C + A.B.C + A.B.C + A.B.C + A.B.C + A.B.C
Simplifies to
= ABC + ABC + ABC + ABC + ABC
Therefore ∑(0,2,3,5,7) = ∏(1,4,6)
Boolean Expressions and Truth Tables
All standard Boolean expressions can be easily converted into truth table format using
binary values for each term in the expression. Standard SOP or POS expressions can also be
determined from a truth table.
Converting SOP expression to Truth Table format
A truth table is a list of possible input variable combinations and their corresponding
output values. An SOP expression having a domain of 2 variables will have a truth table
having 4 combinations of inputs and corresponding output values.
To convert an SOP expression in a Truth table format, a truth table having input
combinations proportional to the domain of variables in the SOP expression is written. Next
the SOP expression is written in a standard SOP form. In the last step all the sum terms
present in the standard SOP expression are marked as 1 in the output.
AB + BC has a domain of three variables thus a truth table having 8 input and output
combinations is required. The SOP expression is converted into standard SOP expression
AB(C + C) + BC(A + A) = ABC + ABC + ABC + ABC = ABC + ABC + ABC + ABC
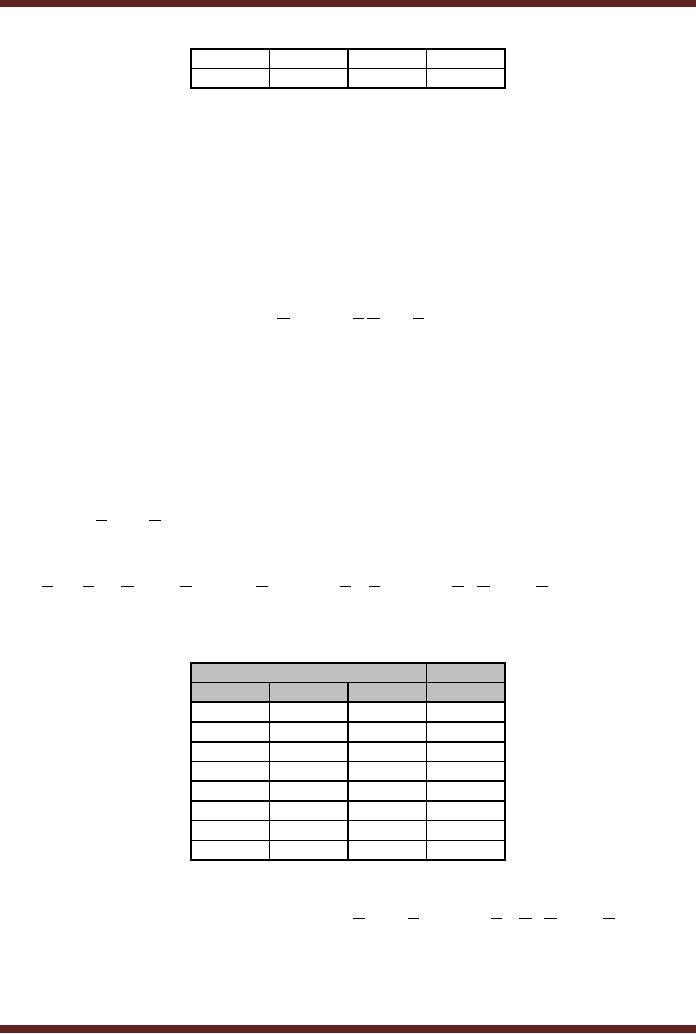
Marking the outputs in the truth table as 1 for sum terms that are present in the standard SOP.
Input
Output
A
B
C
F
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
1
1
0
1
1
87
img
CS302 - Digital Logic & Design
1
1
0
0
1
1
1
1
Table 9.6
Mapping SOP expression to Truth Table
Canonical Sum F= ∑  A,B,C (3,4,5,7) = A.B.C + A.B.C + A.B.C + A.B.C
Converting POS expression to Truth Table format
An POS expression having a domain of 2 variables will have a truth table having 4
combinations of inputs and corresponding output values. To convert a POS expression in a
Truth table format, a truth table having input combinations proportional to the domain of
variables in the POS expression is written. Next the POS expression is written in a standard
POS form. In the last step all the product terms present in the standard POS expression are
marked as 0 in the output.
(A + B)(B + C) has a domain of three variables thus a truth table having 8 input and
output combinations is required. The POS expression is converted into standard POS
expression
(A + B + CC)(AA + B + C) = (A + B + C)(A + B + C)(A + B + C)(A + B + C)
Marking the outputs in the truth table as 0 for product terms that are present in the standard
POS
Input
Output
A
B
C
F
0
0
0
1
0
0
1
0
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
0
1
1
0
1
1
1
1
1
Table 9.7
Mapping POS expression to Truth Table
Canonical Product F= ∏  A,B,C (1,2,3,5) = (A + B + C)(A + B + C)(A + B + C)(A + B + C)
88
Table of Contents:
  1. AN OVERVIEW & NUMBER SYSTEMS
  2. Binary to Decimal to Binary conversion, Binary Arithmetic, 1’s & 2’s complement
  3. Range of Numbers and Overflow, Floating-Point, Hexadecimal Numbers
  4. Octal Numbers, Octal to Binary Decimal to Octal Conversion
  5. LOGIC GATES: AND Gate, OR Gate, NOT Gate, NAND Gate
  6. AND OR NAND XOR XNOR Gate Implementation and Applications
  7. DC Supply Voltage, TTL Logic Levels, Noise Margin, Power Dissipation
  8. Boolean Addition, Multiplication, Commutative Law, Associative Law, Distributive Law, Demorgan’s Theorems
  9. Simplification of Boolean Expression, Standard POS form, Minterms and Maxterms
  10. KARNAUGH MAP, Mapping a non-standard SOP Expression
  11. Converting between POS and SOP using the K-map
  12. COMPARATOR: Quine-McCluskey Simplification Method
  13. ODD-PRIME NUMBER DETECTOR, Combinational Circuit Implementation
  14. IMPLEMENTATION OF AN ODD-PARITY GENERATOR CIRCUIT
  15. BCD ADDER: 2-digit BCD Adder, A 4-bit Adder Subtracter Unit
  16. 16-BIT ALU, MSI 4-bit Comparator, Decoders
  17. BCD to 7-Segment Decoder, Decimal-to-BCD Encoder
  18. 2-INPUT 4-BIT MULTIPLEXER, 8, 16-Input Multiplexer, Logic Function Generator
  19. Applications of Demultiplexer, PROM, PLA, PAL, GAL
  20. OLMC Combinational Mode, Tri-State Buffers, The GAL16V8, Introduction to ABEL
  21. OLMC for GAL16V8, Tri-state Buffer and OLMC output pin
  22. Implementation of Quad MUX, Latches and Flip-Flops
  23. APPLICATION OF S-R LATCH, Edge-Triggered D Flip-Flop, J-K Flip-flop
  24. Data Storage using D-flip-flop, Synchronizing Asynchronous inputs using D flip-flop
  25. Dual Positive-Edge triggered D flip-flop, J-K flip-flop, Master-Slave Flip-Flops
  26. THE 555 TIMER: Race Conditions, Asynchronous, Ripple Counters
  27. Down Counter with truncated sequence, 4-bit Synchronous Decade Counter
  28. Mod-n Synchronous Counter, Cascading Counters, Up-Down Counter
  29. Integrated Circuit Up Down Decade Counter Design and Applications
  30. DIGITAL CLOCK: Clocked Synchronous State Machines
  31. NEXT-STATE TABLE: Flip-flop Transition Table, Karnaugh Maps
  32. D FLIP-FLOP BASED IMPLEMENTATION
  33. Moore Machine State Diagram, Mealy Machine State Diagram, Karnaugh Maps
  34. SHIFT REGISTERS: Serial In/Shift Left,Right/Serial Out Operation
  35. APPLICATIONS OF SHIFT REGISTERS: Serial-to-Parallel Converter
  36. Elevator Control System: Elevator State Diagram, State Table, Input and Output Signals, Input Latches
  37. Traffic Signal Control System: Switching of Traffic Lights, Inputs and Outputs, State Machine
  38. Traffic Signal Control System: EQUATION DEFINITION
  39. Memory Organization, Capacity, Density, Signals and Basic Operations, Read, Write, Address, data Signals
  40. Memory Read, Write Cycle, Synchronous Burst SRAM, Dynamic RAM
  41. Burst, Distributed Refresh, Types of DRAMs, ROM Read-Only Memory, Mask ROM
  42. First In-First Out (FIFO) Memory
  43. LAST IN-FIRST OUT (LIFO) MEMORY
  44. THE LOGIC BLOCK: Analogue to Digital Conversion, Logic Element, Look-Up Table
  45. SUCCESSIVE –APPROXIMATION ANALOGUE TO DIGITAL CONVERTER