LOGIC GATES: AND Gate, OR Gate, NOT Gate, NAND Gate

<< Octal Numbers, Octal to Binary Decimal to Octal Conversion

AND OR NAND XOR XNOR Gate Implementation and Applications >>

CS302 - Digital Logic & Design

Lesson No. 05

LOGIC GATES

The Digital Systems should be able to process or perform operations on the numbers

that are represented in the Binary Number System. The simplest operations that come to mind

are the arithmetic operations like add and subtract. There are many more operations and

functions that Digital Systems are able to perform.

Digital Logic Gates provide the basic building blocks; these Logic Gates perform

different operations on the Binary information. These Logic Gates are used in different

combinations to implement large complex systems. Digital Logic Gates are represented and

identified by unique symbols. These symbols are used in circuit diagrams to describe the

function of a digital circuit.

Digital Logic Gates function is represented by a function table or a truth table that

describes all the Logic gate outputs for every possible combination of inputs. As the logic

Gates operate on binary values therefore these function tables describes the relationship

between the input and output in terms of binary values. The function of a Logic Gate is also

described in terms of an expression.

Logic Gates are practically used in circuits where the inputs to the Logic Gates vary in

time. Timing diagrams are used to describe the response of the Logic Gates in a certain period

of time with respect to the changing input. Timing diagrams graphically show the actual

performance (behavior) of the logic gate to the changing inputs for a predetermined period of

time or sequence of input signals.

The three fundamental Gates are the AND, OR and NOT Gates.

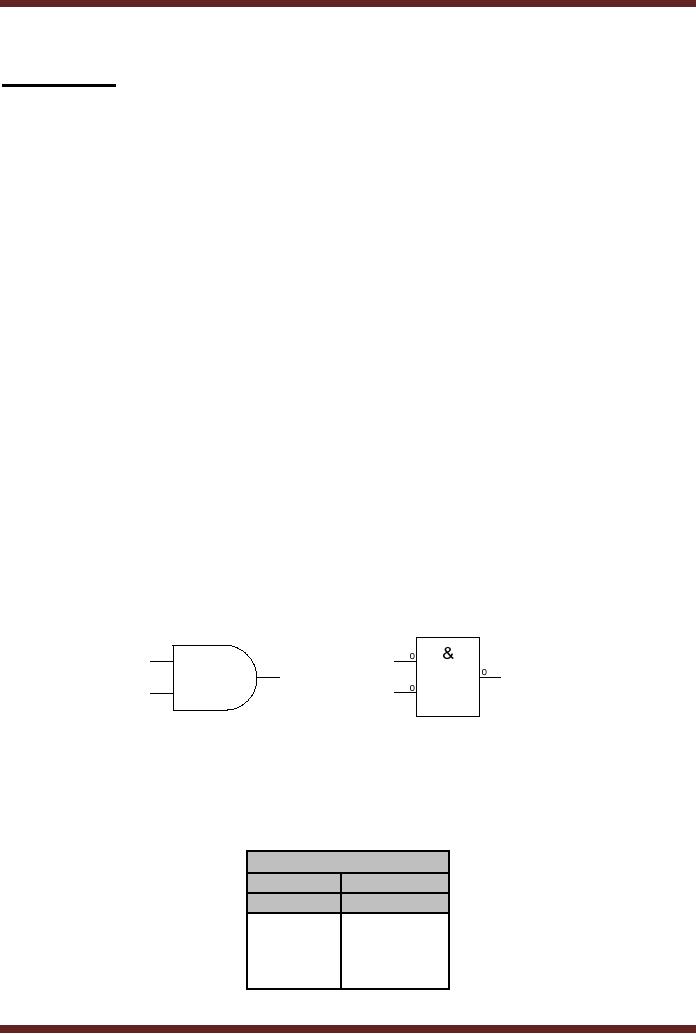
AND Gate

The AND Gate performs a logical multiplication function. An AND Gate has multiple

inputs and a single output. Most commonly used AND Gates are two input AND gates. An

AND Gate is represented by the symbols shown in Figure 5.1

Figure 5.1

Symbolic representation of AND Gate

The multiplication function performed by the AND Gate is shown in the function table

for a two input AND Gate. Figure 5.2. The function table for a 3, 4 or multiple input AND Gate

is similar. The output is 1 when all the inputs are at logic level 1. For all other input

combinations the output is zero.

Logical AND Operation

Inputs

Output

Figure 5.2

Function Table of an AND Gate

CS302 - Digital Logic & Design

The expression describing the operation of a two inputs AND Gate is F = A.B

The `.' is an AND Operator and the expression represents an AND operation between inputs A

and B. Expression for multiple input AND Gates is F = A.B.C. ⋅ ⋅ ⋅ N , where N is the total

number of inputs.

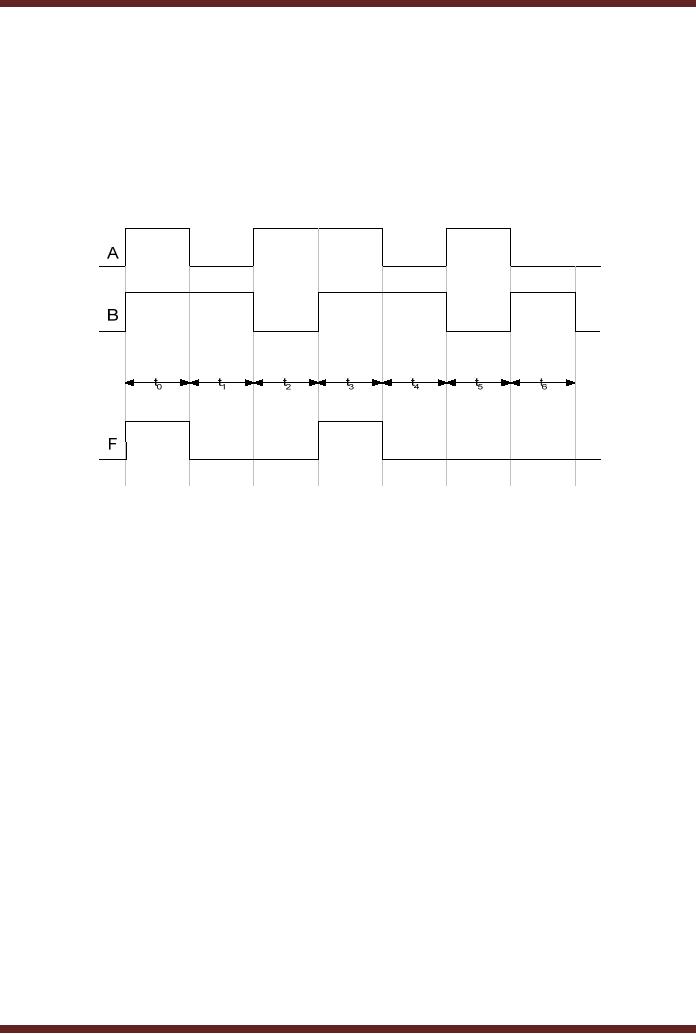
The timing diagram of the two input AND gate with the input varying over a period of 7

time intervals is shown in the diagram. Figure 5.3.

Figure 5.3

Timing diagram of operation of an AND gate

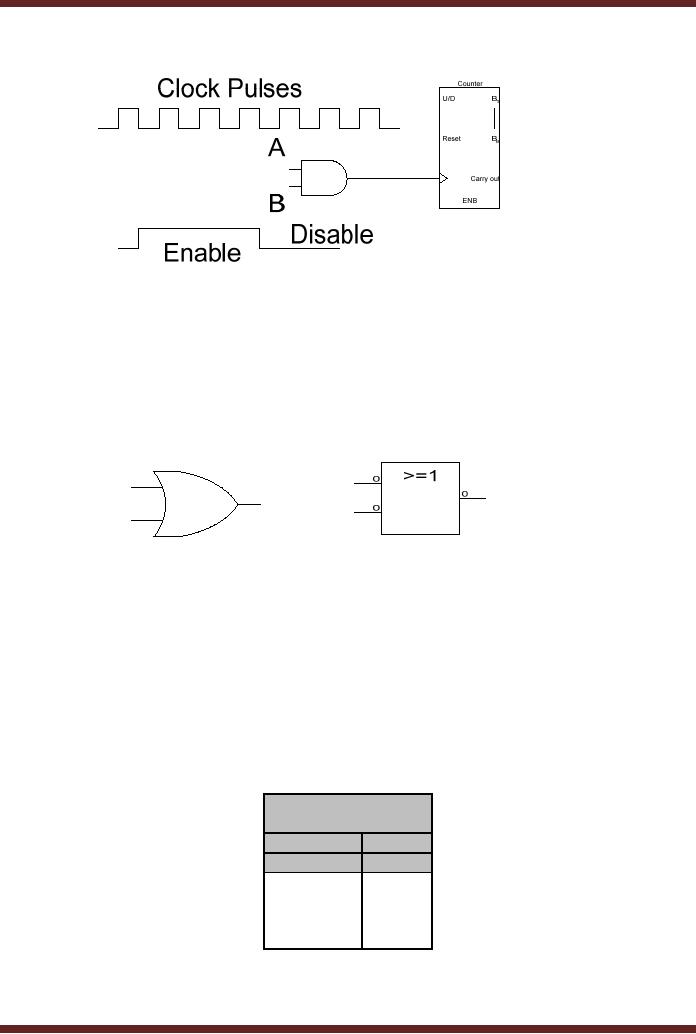
An important use of an AND gate in addition to the multiplication operation is its use to

disable or enable a device. Figure 5.4. A Counter device counts from 0 to 100. The counter

device increments its current count value to the next when it receives a pulse at its clock input.

To allow the Counter device to count continuously from 0 to 100, continuous pulses are

applied at the clock input of the Counter Device. The continuous pulses are shown as Clock

pulses.

The counter can be stopped from counting by stopping the clock pulses from reaching

the clock input of the Counter Device. A 2-input AND gate is connected to the Counter Clock

input. The clock pulses are applied at the Input A of the AND Gate. Input B of the AND Gate is

connected to an Enable/Disable signal. When the Counter Device is stopped from counting the

enable/disable signal ay Input B is set to 0.

The Function Table, figure 5.2, indicates that when ever an input of the AND gate is set

to 0 the output also becomes 0. Thus by applying the disable signal 0 at Input B, the output of

the gate becomes zero and therefore clock signals are prevented from reaching the Counter

device. To allow the Counter Device to count, the enable/disable signal at input B of the AND

gate is set to 1. The Function Table of the AND gate indicates that when an Input of the AND

gate is 1, the output follows the input signal applied at the input A of the AND Gate. Thus the

clock signal at Output of the AND gate follows the clock signal at Input A of the AND Gate.

CS302 - Digital Logic & Design

Figure 5.4

Enabling a Counter using an AND Gate

OR Gate

The OR Gate performs a Boolean add function. An OR Gate has multiple inputs and a

single output. Most commonly used OR Gates are two input OR gates. An OR Gate is

represented by symbols as shown in figure 5.5.

Figure 5.5

Symbolic representation of OR Gate

The addition function performed by the OR Gate is shown in the function table for a two

input OR Gate. Figure 5.6. The function table for a 3, 4 or multiple input OR Gate is similar.

The output is 1 when any one input is at logic level 1. The output is 0 when all inputs are zero.

The expression describing the operation of the two inputs OR Gate is F = A + B . The

`+' is an OR Operator and the expression represents an OR operation between inputs A and B.

Expression for multiple input OR Gates is F = A + B + C + .....N , where N is the total number of

inputs.

Logical OR

Operation

Inputs

Output

Figure 5.6

Function Table of an OR Gate

CS302 - Digital Logic & Design

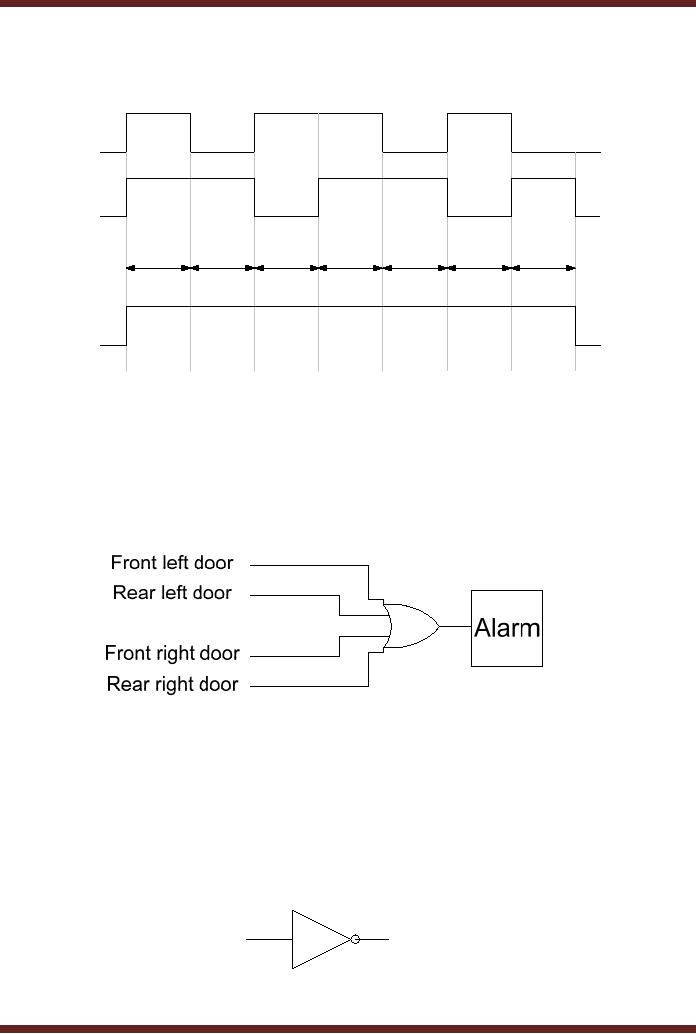
The timing diagram of the two input OR gate with the input varying over a period of 7

time intervals is shown in the diagram 5.7.

Figure 5.7

Timing diagram of operation of an OR gate

The OR Gate is used in applications where the output signal is a 1 when any one input

is a 1. An example of such an application is an alarm circuit for car door locks shown in

diagram, figure 5.8. Four circuits are connected to each of the four doors of a car. The door

circuit generates a 1 when the door is open and a 0 when it is closed. The four outputs of each

of the four door circuits are connected to the four inputs of an OR Gate. The output of the OR

gate is connected to an Alarm.

Figure 5.8

Car door Alarm System based on a 4-input OR Gate

When any one or more doors are open the inputs of the OR Gate have a 1. The output

of the OR gate is a 1, according to the Function Table of an OR Gate, figure 5.6, which

enables the Alarm.

NOT Gate

NOT Gate is also known as an Inverter. The name indicates that the NOT Gate should

be performing an inversion function. The Not Gate has a single input and a single output. The

NOT Gate is represented by the symbol shown in Figure 5.9.

Figure 5.9

NOT Gate

CS302 - Digital Logic & Design

The input signal applied across the single input of the OR gate is inverted and is

available at the output. The function of the NOT Gates is described by the Function Table or

the Truth Table represented in Figure 5.10.

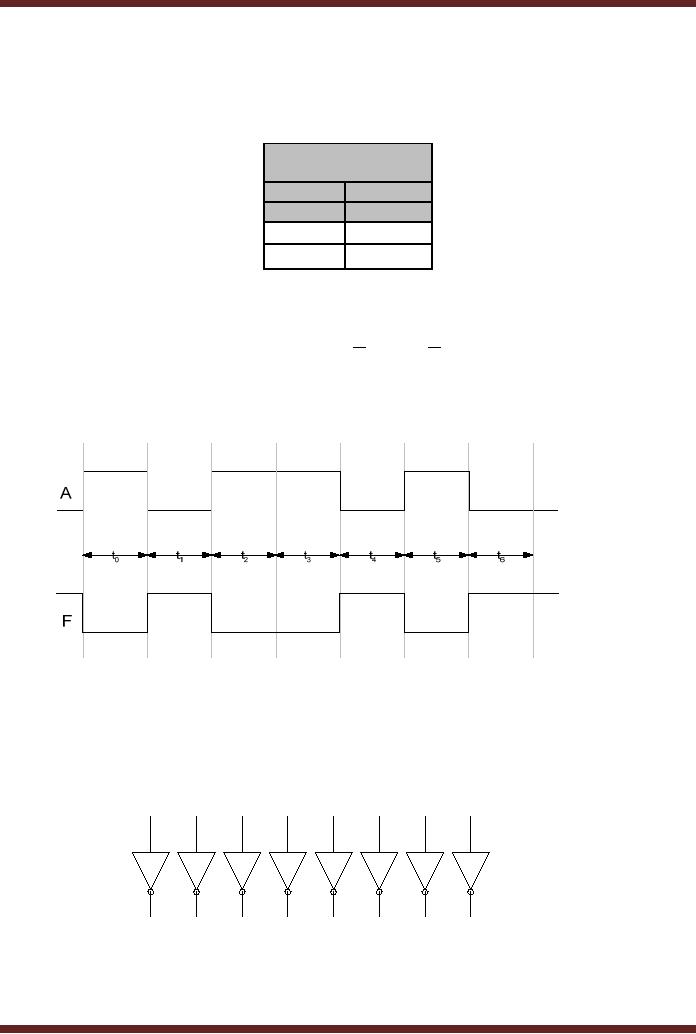
Logical NOT

Operation

Input

Output

Figure 5.10

Function Table of a NOT Gate

The expression describing the behavior of a NOT gate in terms of the Input and Output

shown in the Function Table, Figure 5.10 is F = A where A indicates invert of A

The timing diagram of a NOT gate with the input varying over a period of 7 time

intervals and its corresponding output is shown in the Figure 5.11.

Figure 5.11

Timing diagram of operation of a NOT gate

The NOT Gate is used in circuits to generate the 1's Complement of a number by

inverting all its bits. Figure 5.12. It is also used to invert an incoming signal `1' as per

requirements of another circuit which requires the signal to be `0'.

Figure 5.12

A 1's Complement Circuit using 8 NOT Gates

CS302 - Digital Logic & Design

In addition to the three Fundamental Gates which perform AND, OR and NOT operations, two

other important gates that are commonly used in Digital Logic are the NAND and NOR Gates.

These two gates do not perform any new functions. The NAND Gate performs an AND-NOT

function and the NOR gate performs the OR-NOT function.

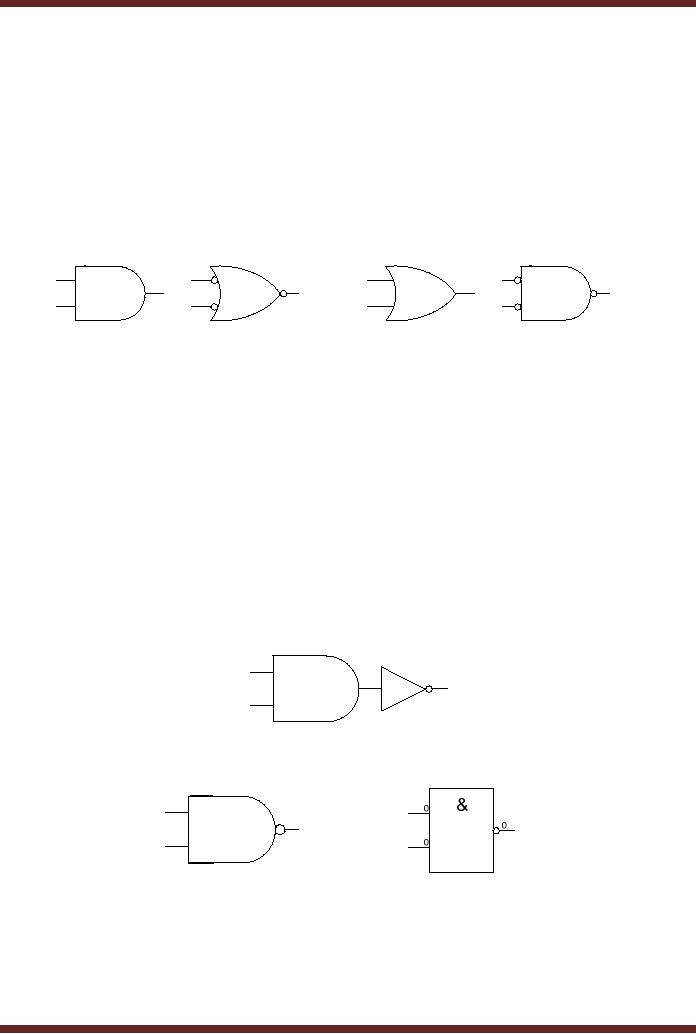
AND & OR Gate alternate symbols

The AND gate and the OR gate can also be represented by alternate symbols. The two

fundamental symbols, the AND Gate symbol and the OR gate symbol complement each other.

Thus a gate can be represented by its complementary symbol. The inputs and outputs of the

complementary symbol are inverted by placing or removing bubbles. Figure 5.13.

Figure 5.13

Alternate Symbolic representation of AND & OR gates

The AND gate is represented by its complementary OR gate symbol, the two inputs

and the output are inverted by placing bubbles. The OR gate is represented by its

complementary AND gate symbol, the two inputs and the output are inverted by placing

bubbles.

NAND Gate

The NAND Gate performs a function that is equivalent to the function performed by the

combination of an AND gate and a NOT gate. Figure 5.14

A NAND Gate has multiple inputs and a single output. Most commonly used NAND

Gates are two input NAND gates. A NAND gate is represented by the symbols shown in figure

5.15, the NOT gate connected at the output of the AND gate is represented by a circle, in

Digital Logic terminology a `bubble'.

Figure 5.14

NAND Gate function

Figure 5.15

Symbolic representation of NAND Gate

The function performed by the NAND Gate is described by the Function Table for a two

input NAND Gate. Figure 5.16. The function table for a 3, 4 or multiple input NAND Gate is

CS302 - Digital Logic & Design

similar. The output is 0 when all inputs are 1s. For all other combinations of inputs the output

logic level is 1.

Logical NAND

Operation

Inputs

Output

Figure 5.16

Function Table of a NAND Gate

The expression describing the operation of the two inputs NAND Gate is F = A.B .

Expression for multiple input NAND Gates is F = A.B.C......N , where N is the total number of

inputs.

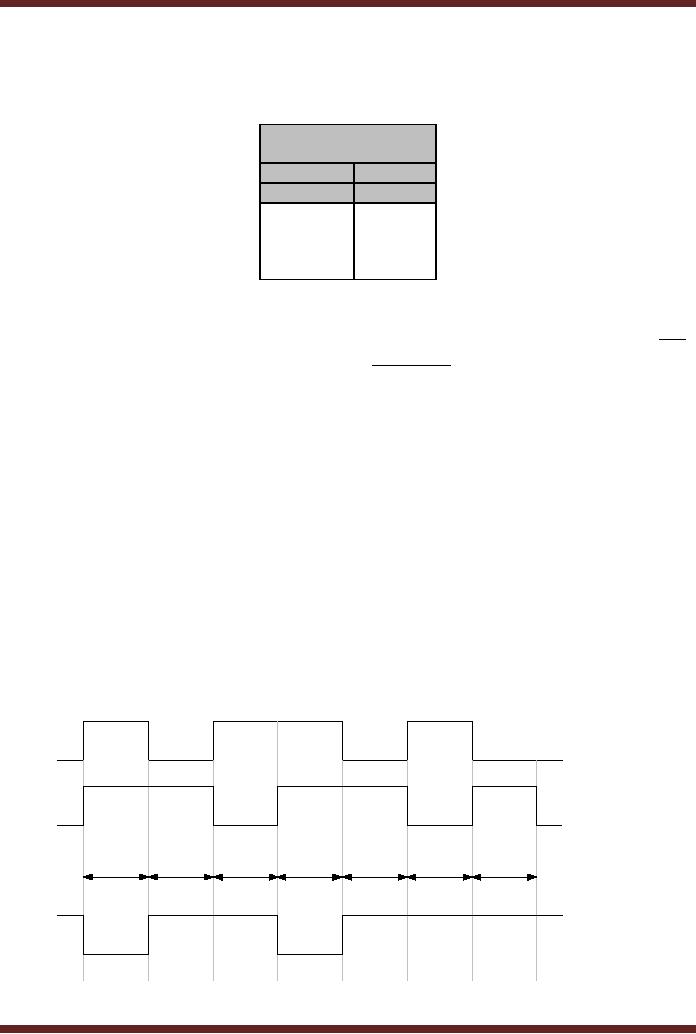
The timing diagram of the two input NAND gate with the input varying over a period of

7 time intervals is shown in the diagram. Figure 5.17.

NAND Gate as a Universal Gate

The NAND gate is also used as a Universal Gate as the NAND Gate can be used in a

combination to perform the function of a AND, OR and NOT gates.

1. NOT Gate Implementation

A NOT gate can be implemented using a NAND gate by connecting both the inputs of the

NAND gate together. By connecting the two inputs together, the input combinations where the

inputs are dissimilar become redundant. The Function Table of the 2-input NAND Gate

reduces to that of the NOT gate. Figure 5.18

Figure 5.17

Timing diagram of operation of a NAND gate

CS302 - Digital Logic & Design

Logical NAND

Operation

Inputs

Output

Figure 5.18

Implementing a NOT Gate using a NAND gate

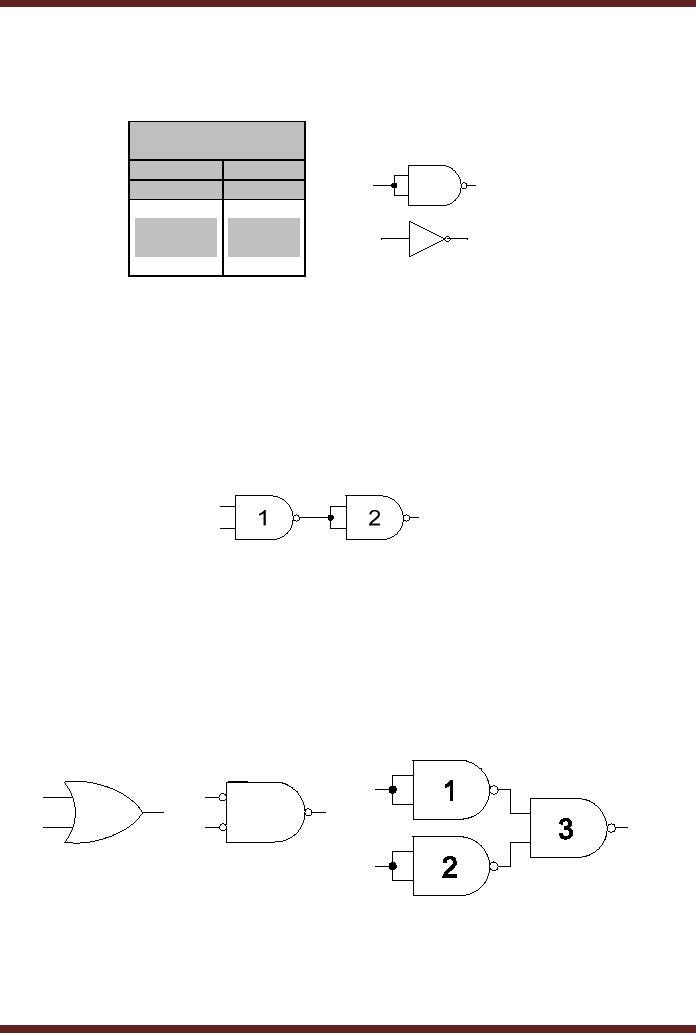
2. AND Gate Implementation

A NAND Gate performs the AND-NOT function. Removing the NOT gate at the output

of the NAND gate results in an AND gate. The effect of the NOT gate at the output of the

NAND gate can be cancelled by connecting a NOT gate at the output of the NAND Gate. The

two NOT gates cancel each other out. A NOT Gate implemented using a NAND gate (2) is

connected to the output of a NAND gate (1). Figure 5.19.

Figure 5.19

Implementing an AND Gate using two NAND gates

3. OR Gate Implementation

An OR Gate can be implemented using a combination of three NAND gates. The

implementation is based on the alternate symbolic representation of the OR gate. The OR

gate is represented as an AND gate with bubbles at the inputs and outputs. Figure 5.13. The

two bubbles at the input can be replaced by two NOT gates (1) & (2) implemented using two

NAND gates. If the two bubbles are removed from the two inputs, the AND gate with the

bubble at the output represents a NAND gate (3). Figure 5.20

Figure 5.20

Implementing an OR Gate using three NAND gates

NOR Gate

The NOR Gate performs a function that is equivalent to the function performed by a

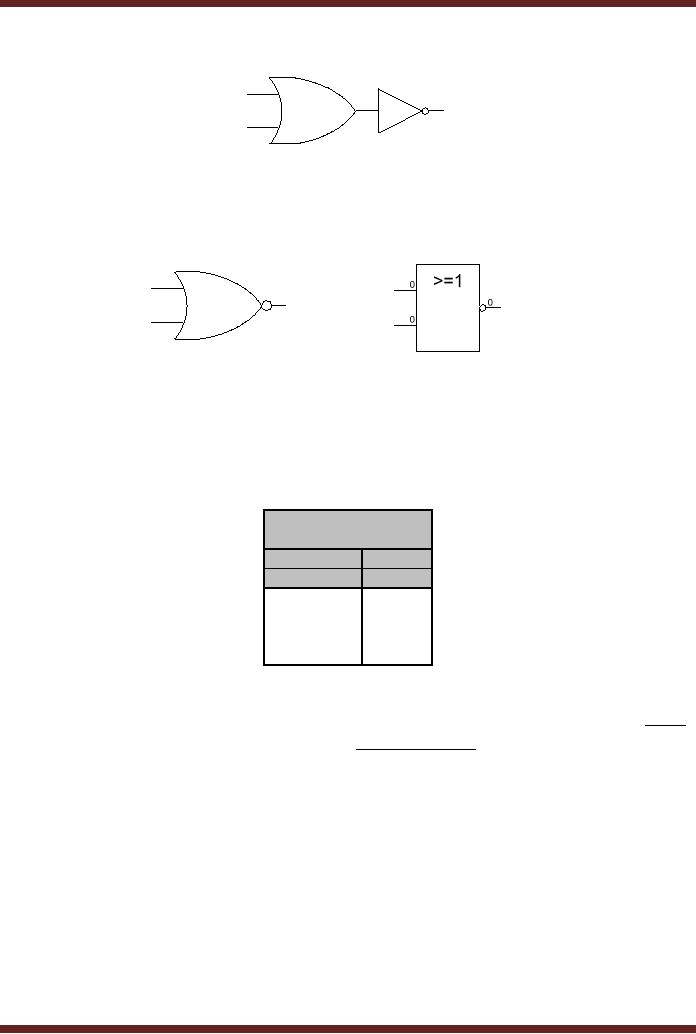
combination of an OR gate and a NOT gate. Figure 5.21

CS302 - Digital Logic & Design

Figure 5.21

NOR Gate function

A NOR Gate has multiple inputs and a single output. Most commonly used NOR Gates

are two input NOR gates. A NOR gate is represented by the symbols shown in figure 5.22, the

NOT gate connected at the output of the OR gate is represented by a circle.

Figure 5.22

Symbolic representation of NOR Gate

The function performed by the NOR Gate is described by the Function Table for a two

input NOR Gate. Figure 5.23. The function table for a 3, 4 or multiple input NOR Gate is

similar. The output is 1 when all inputs are 0s. For all other combinations of inputs the output

logic level is 0.

Logical NOR

Operation

Inputs

Output

Figure 5.23

Function Table of a NOR Gate

The expression describing the operation of the two inputs NOR Gate is F = A + B .

Expression for multiple input NOR Gates is F = A + B + C + .....N , where N is the total number

of inputs.

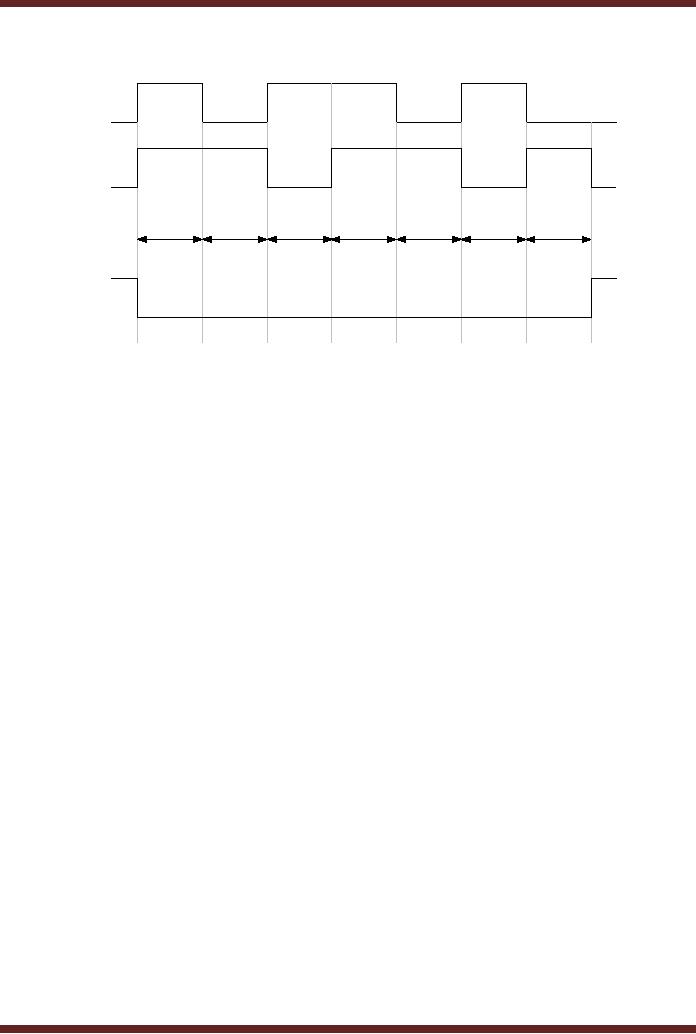
The timing diagram of the two input NOR gate with the input varying over a period of 7

time intervals is shown in the diagram. Figure 5.24.

CS302 - Digital Logic & Design

Figure 5.24

Timing diagram of operation of a NOR gate

Table of Contents: