THE LOGIC BLOCK: Analogue to Digital Conversion, Logic Element, Look-Up Table

<< LAST IN-FIRST OUT (LIFO) MEMORY

SUCCESSIVE –APPROXIMATION ANALOGUE TO DIGITAL CONVERTER >>

CS302 - Digital Logic & Design

Lesson No. 44

THE LOGIC BLOCK

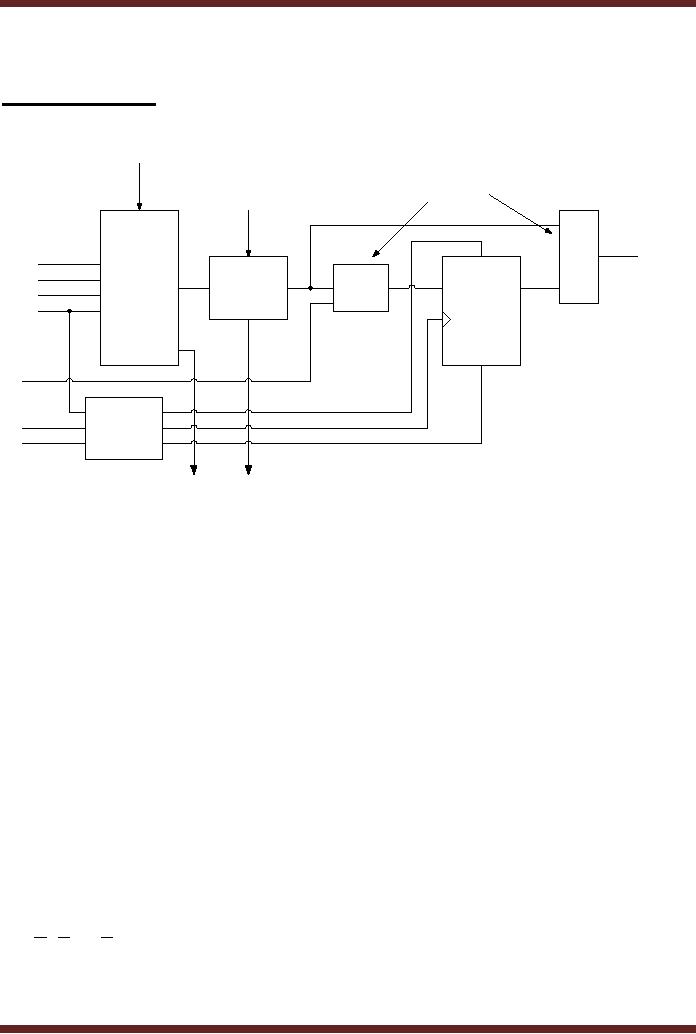
Each Logic Block consists of a several Logic elements. The details of the Logic

Element are shown in figure 44.1.

Programmable

Carry In

Select

Interconnect

Data from

Cascade

programmable

interconnects

Look

Cascade

Logic

Table

Flip-Flop

Clock/Clear/

Preset

Select

Logic

Carry

Cascade

Out

Figure 44.1

Block diagram of a Logic Element

The Logic Element

The Look-Up Table LUT has 4-inputs and can be programmed as a logic function

generator. The LUT can be programmed to produce SOP functions or logic functions such as

adders and comparators. When the LUT is configured as an adder the Carry In and Carry Out

inputs and outputs allow for adder expansion by connecting more adders. The Cascade Logic

allows one LUT to be cascaded with another LUT in other logic units. There are two

Programmable selects, the first Programmable selects allows selection of either the

combinational functions from the LUT output or a direct input to be connected to the input of a

flip-flop. The second Programmable select allows selection of the combinational function from

the LUT output or the registered functions from the flip-flop output. The clock/Clear/Preset

Select Logic controls the operation of the flip-flop through the Clear and Select Asynchronous

signals and the Clock Synchronous signal.

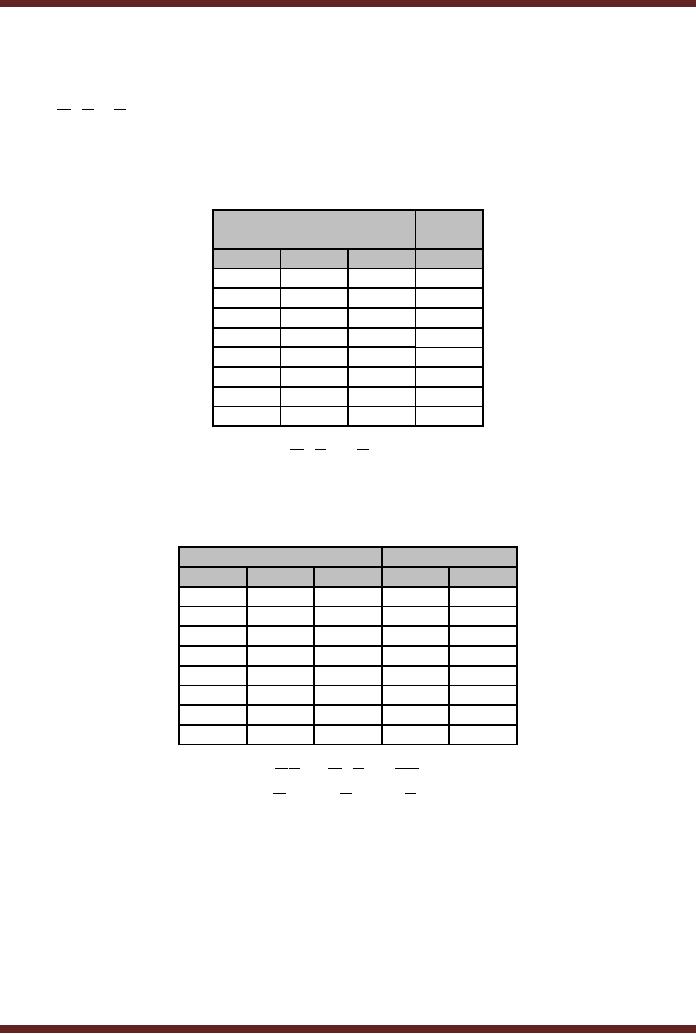
The Look-Up Table

The Look-Up Table shown in the Logic Element is implemented using a memory

element that can be programmed to implement different logic functions. Two examples of LUT

programmed to generate a logic function and to implement a full-adder are shown. Table 44.1

In the first example illustrated by Table 44.1a a three variable SOP function

F = ABC + ABC + ABC is implemented. A memory having 8 locations and storing a single bit

value at each location is required to implement the three variable function. The three bit

address lines which are used to select one out of eight memory locations represents the three

function variables A, B and C respectively. The product terms that are included in the function

439

CS302 - Digital Logic & Design

are represented by memory locations that store logic 1 binary value. The product terms or the

Min-terms that are missing from the function are represented by memory locations that store

logic 0 value. In the function shown, memory locations 2, 5 and 7 which represent the product

terms ABC, ABC and ABC respectively have logic 1 values stored. Thus when ever

addresses 2, 5 or 7 are issued, the data output is a 1 for all other addresses the data output is

a 0.

Address Input

Data

Output

F = ABC + ABC + ABC

Table 44.1a

LUT programmed to generate a function

Address Input

Data Output

Cin

Sum

Cout

Sum = ABC + ABC + ABC + ABC

C out = ABC + ABC + ABC + ABC

Table 44.1b

LUT Programmed as Full-Adder

A Single bit Full-Adder can be similarly implemented by using a memory which has

three storage locations, each location storing two bits. A single bit full-adder has three input

variables A, B and Cin and two output variables Sum and Cout. The three address lines which

select one out of eight memory locations are connected to the three input variables A, B and

Cin. The eight two bit memory locations are programmed to represent the Sum and Cout

functions. An address 110 represents the variables A=1 and B=1 and Cin = 0. The Sum output

440

CS302 - Digital Logic & Design

should be 0 and the Cout should be 1 which is represented by the data output 01 corresponding

to the address 110.

Analogue to Digital Conversion

Digital systems process digital information. The input and the output to the digital

systems is in digital binary format. Real world quantities are in analogue form, which are

converted into digital format for processing by the digital system. The processed digital output

has to be converted back into analogue format. Mobile phones convert the analogue speech

signal into a digital signal which is processed digitally. The digital signal which is received is

converted back to an analogue form which one hears. Digital thermometers measure

temperature which is in analogue form. The analogue signal is converted into digital format

which is displayed in the form of numbers representing the temperature value. Measuring

instruments such as digital voltmeters also sample an electrical signal in its analogue form.

The analogue samples are digitized and displayed in the form of numbers representing voltage

values. CDs which store digital audio and video files have the original audio and video

analogue signals converted into digital format for storage on CDs. To replay the audio or video

file the digital information is converted back into analogue form. Industrial controller system

sample analogue values, digitize the sampled values, process the digitized data and convert

the digitized processed information into corresponding analogue outputs.

Analogue signals are converted into Digital signals by Analogue to Digital (A/D)

converters. The conversion of the analogue signal into a corresponding digital signals is done

by first sampling the analogue signal and holding it stable for the A/D converter to convert the

signal into a digital value.

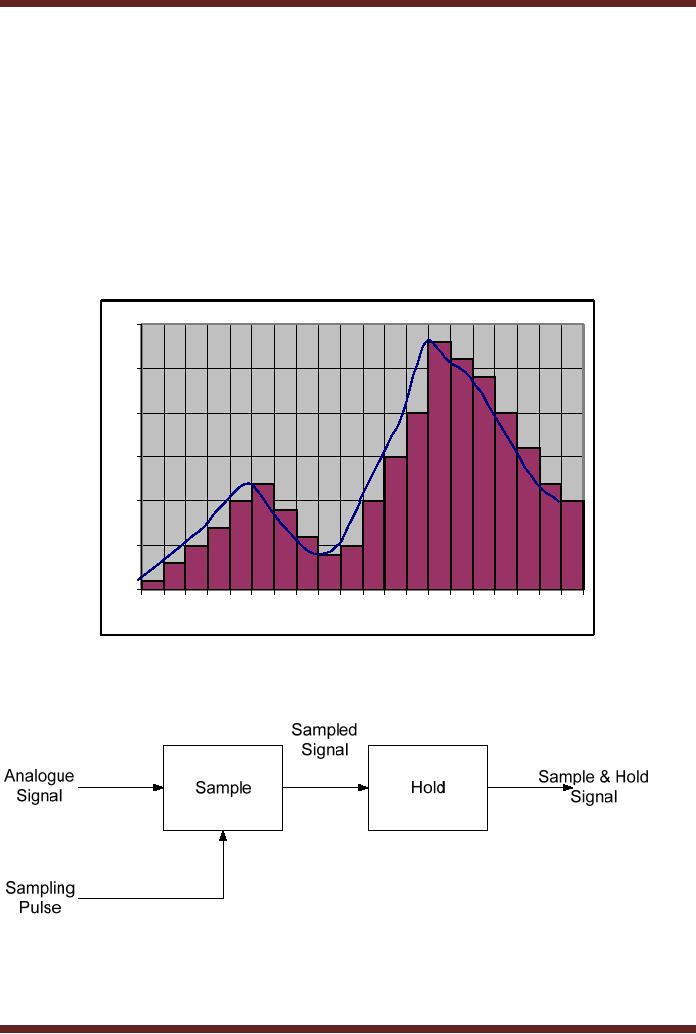
Sample and Hold Operation

A sample and hold circuit performs two important operations. The analogue signal is

sampled at regular sampling intervals to take sufficient number of discreet values at points on

the analogue waveform. The more samples are taken the more accurate is the representation

of the original analogue signal. The sampling frequency according to the Nyquist Criteria

should be twice the maximum frequency of the highest analogue frequency. A sampled value

has to be held stable for a certain minimum time to allow the A/D converter to convert the

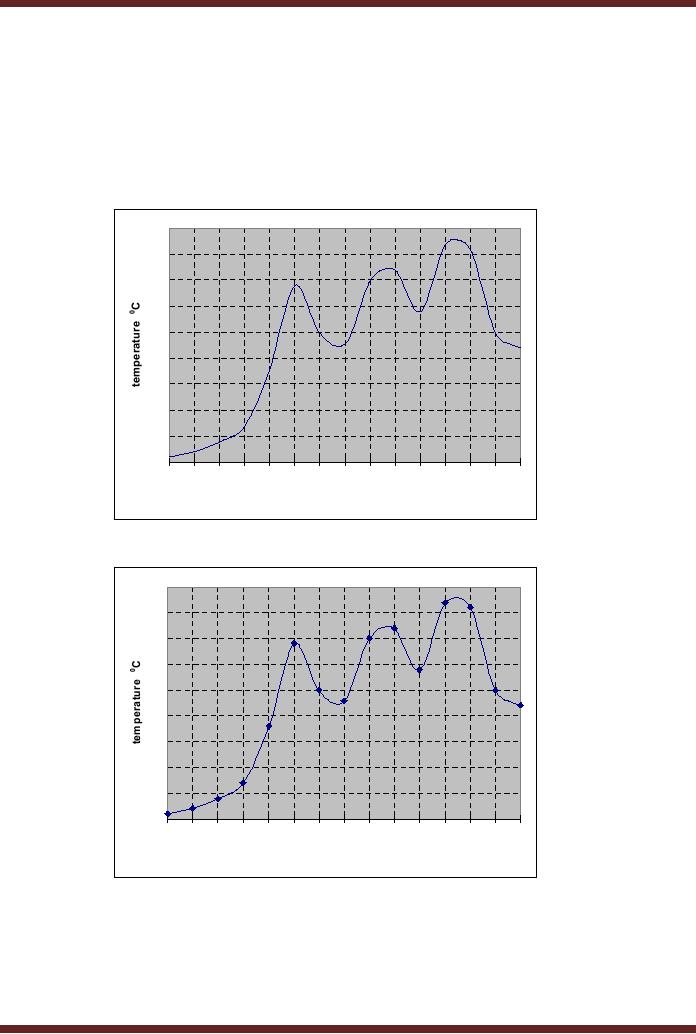
sample values into equivalent digital values. Figure 44.2a shows an input analogue signal

representing temperature varying with time. To convert the analogue signal it is sampled at

regular intervals. The analogue signal which is sampled at 15 equal intervals is shown in figure

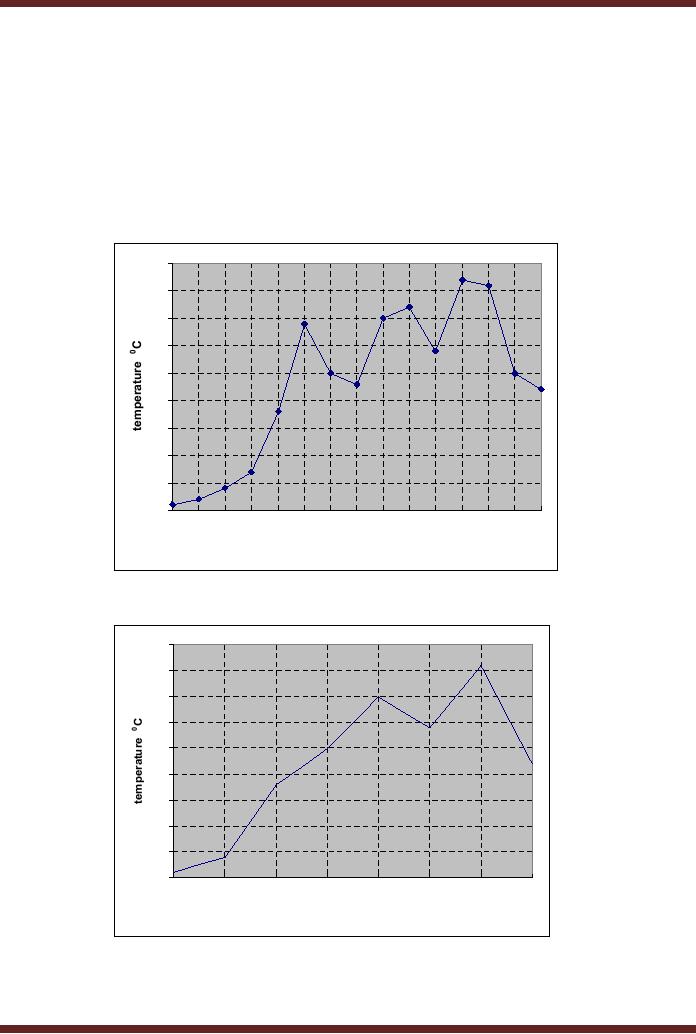
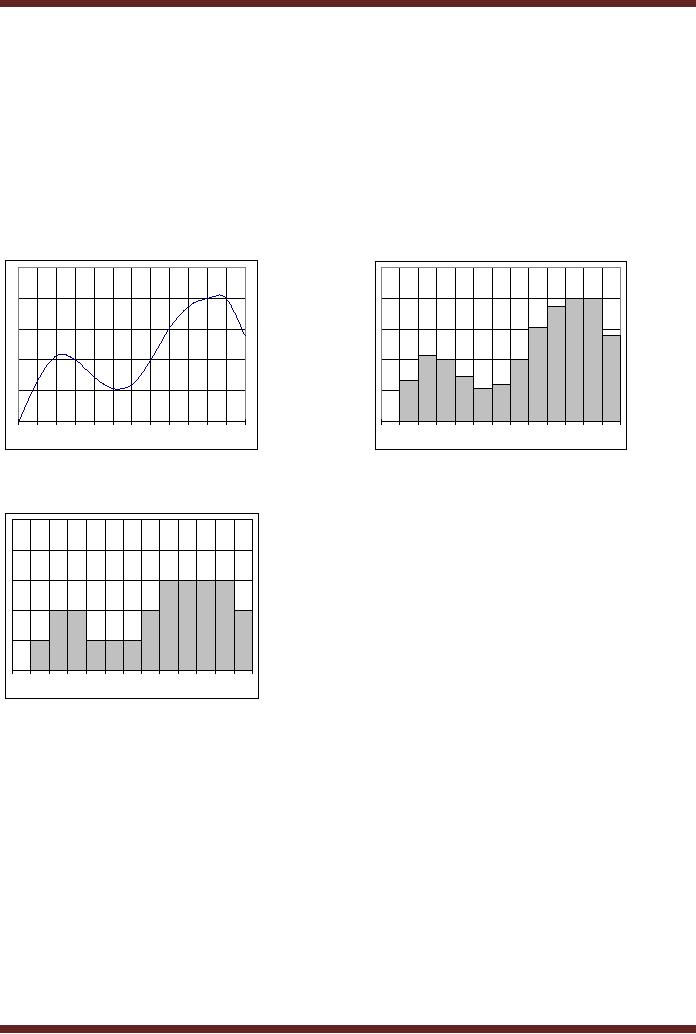
44.2b. The number of samples determine the accuracy of the digitized signal. If the 15

samples are plotted the resulting signal represents reconstructed analogue signal based on

the 15 samples. Figure 44.2c. The reconstructed signal is not an exact replica of the original

analogue signal but is similar. The exactness of the reconstructed signal depends upon the

number of samples. If the number of samples are few then the reconstructed signal losses its

resemblance to the original signal. Figure 44.2d. The signal with fewer samples then the

desired number of samples that are required to accurately reconstruct the signal is known as

an under sampled signal. The under sampled signal is shown to lose the information in the

original signal when it is reconstructed. If the original signal is over sampled by increasing the

number of samples beyond 15, the reconstructed signal will be a very accurate representation

of the original signal however processing too many samples may require too much processing

time.

441

CS302 - Digital Logic & Design

time

Figure 44.2a

Continuous signal showing temperature varying with time

time

Figure 44.2b Sampling the Continuous Signal at 15 equal intervals

442

CS302 - Digital Logic & Design

samples

Figure 44.2c Reconstructed Signal by plotting 15 sampled values

samples

Figure 44.2d Reconstructed Signal by plotting 7 sampled values

443

CS302 - Digital Logic & Design

The number of samples that are essential to accurately represent the original signal is

determined by the Nyquist Criteria which requires that the sampling frequency should be twice

the frequency of the sampled signal. Assuming the original signal to have a frequency of 50

Hz, the sampling which allows accurate reconstruction of the signal should be carried out at

100 Hz.

The sampled signal at Nyquist frequency have to be held stable for a minimum time

period to allow the A/D converter to convert the analogue sample into a digital value. If the

sampled signal is not held stable, the A/D converted would not have enough time to accurately

convert the signal into a digital value. The samples that are held stable for converting into

digital values by the sample and hold circuit are depicted by a staircase signal shown in figure

44.3.

9 10 11 12 13 14 15 16 17 18 19 20

Figure 44.3a Sample and Hold signal

Figure 44.3b Sample and Hold Circuit

Quantization

444

CS302 - Digital Logic & Design

The process of converting the analogue signal into a digital representation (code) is

known as quantization. The number of bits that are used to represent the digital code

determine the accuracy of the digitized signal. An analogue 220 volt signal can be represented

in digital terms by a 2-bit binary number. The four possible digital values 00, 01, 10 and 11

represent four levels of the input 220 volt analogue signal. The binary value 00 represents 0

volts, 01 represents 73 volts, 10 represents 146 volts and 11 represents 220 volts. Since four

values can be represented, therefore analogue voltages in the ranges 37 to 109 are

represented by binary 01. Similarly voltage ranges between 110 to 183 are represented by

binary 10. If a three bit representation is used then the range of analogue signals represented

by the eight, 3-bit values is reduced thereby increasing the accuracy.

16 15

11 12 13

Figure 44.4a Analogue Signal

Figure 44.4b

Sample & Hold Signal

11 12 13

Figure 44.4c Digitized Signal

In figure 44.4 the representation of an analogue signal using 2 bits or four quantization

levels is shown. The original signal has analogue value range from 0 to a peak value of 31.

Figure 44.4a. The analogue signal is sampled, the output of the Sample and Hold circuit is

shown in figure 44.4b. The sampled values range between 0 and 30. The sampled signal is

digitized using four quantization levels or 2-bits. Figure 44.4c. The original signal having

values in the range 0 to 7.5 are represented by a digital representation 00. Analogue values in

the range 8 to 14.5 are represented by a digital representation 01. Analogue values in the

range 15 to 22.5 are represented by digital representation 10 and the values ranging between

23 and 30 are represented by digits 11. If the quantization level is quadrupled to 16 levels the

digitized representation of the analogue signal becomes more accurate. Figure 44.5.

445

CS302 - Digital Logic & Design

11 12 13

Figure 44.5a Analogue Signal

Figure 44.5b

Sample & Hold Signal

11 12 13

Figure 44.5c Digitized Signal

In figure 44.5, the analogue signal is shown to be digitized using a 16 level

quantization. The digitized signal shown in figure 44.5c closely resembles the analogue signal

as compared to the 4 level quantized signal shown in figure 44.4c.

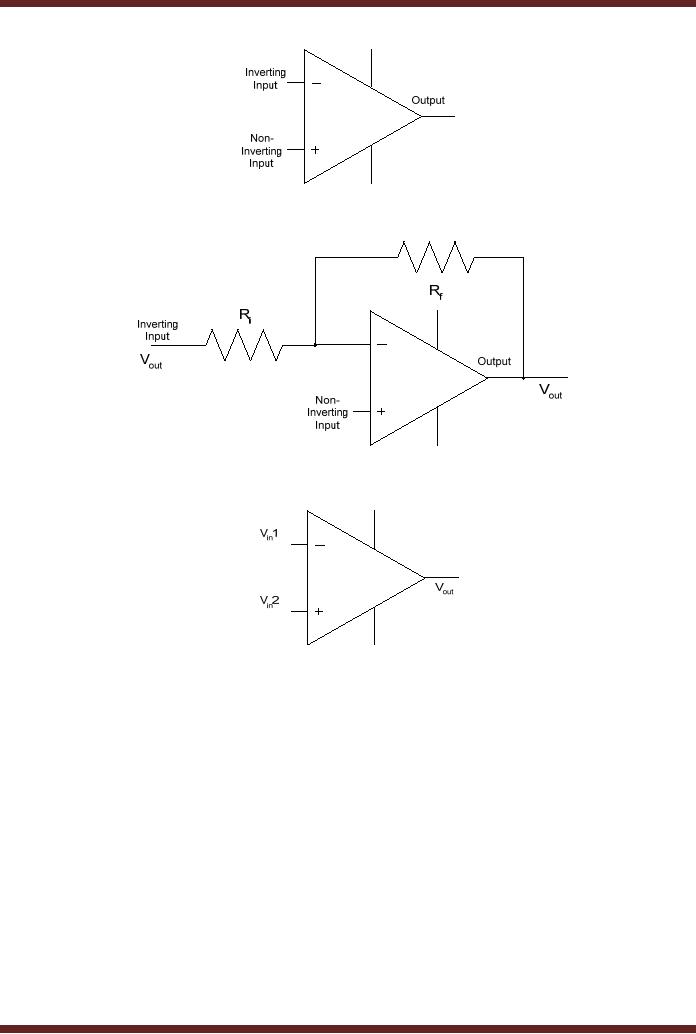
Operational Amplifier (Op-Amp)

Operational Amplifier is a linear amplifier which has two inputs (inverting and non-

inverting) and one output. It has a high voltage gain, high input impedance and low output

impedance. The Op-Amp amplifies the difference signal between its inverted and non-inverted

inputs. Figure 44.6a

The Op-Amp is used as an inverting amplifier and as a comparator. When the Op-Amp

is used as an inverting amplifier, the input signal is applied at its Inverted input through a

series resistance Ri. The output of the Op-Amp is connected to the inverted input through a

feedback resistance Rf. Figure 44.6b. The voltage gain of the Inverting Amplifier is given by

the relation

Vout/Vin = - Rf/Ri

When the Op-Amp is used as a comparator two voltages are applied at the inputs,

when these voltages differ by a very small amount the output of the Op-Amp is driven into one

of its two saturated output sates logic high or low depending upon which of the two input

voltages is higher. Figure 44.6c

446

CS302 - Digital Logic & Design

Figure 44.6a Op-Amp

Figure 44.6b Op-Amp as an Inverting Amplifier

Figure 44.6c Op-Amp as a Comparator

Analogue to Digital converters use Op-Amps as an Integrator and Comparator. An

Integrator integrates the input voltage. An Integrator is implemented by replacing the feedback

resistance Rf by a Capacitor.

Flash Analogue-to Digital Converter

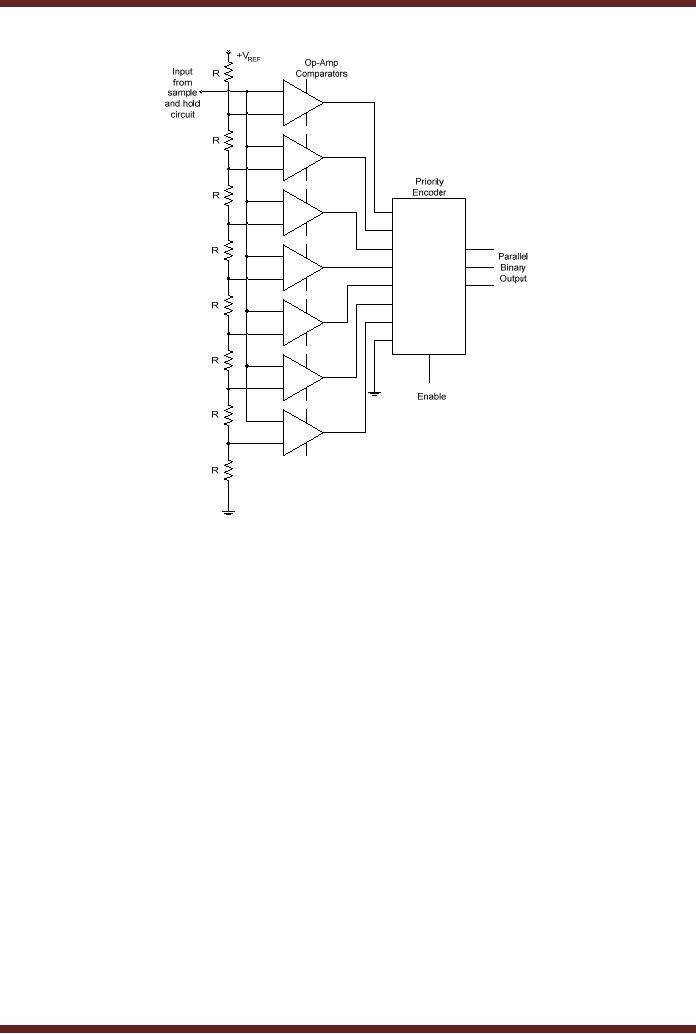
The Flash A/D converter is based on a resistor potential divider, where multiple

resistors of identical value form a voltage divider. A reference voltage is applied at one end of

the potential divider which divides the voltage equally across all the resistors. The input

analogue voltage is applied at the non-inverting inputs of a set of Op-Amp based comparators.

The inverting input of each comparator is connected to the resistive voltage divider which

provides reference voltages for all the comparators. If the input voltage is larger than the

reference voltage the output of the comparator is logic high otherwise it is logic low. The

outputs of all the comparators are connected to the input of a priority encoder which converts

the comparator outputs to a binary coded equivalent value. Figure 44.7a.

447

CS302 - Digital Logic & Design

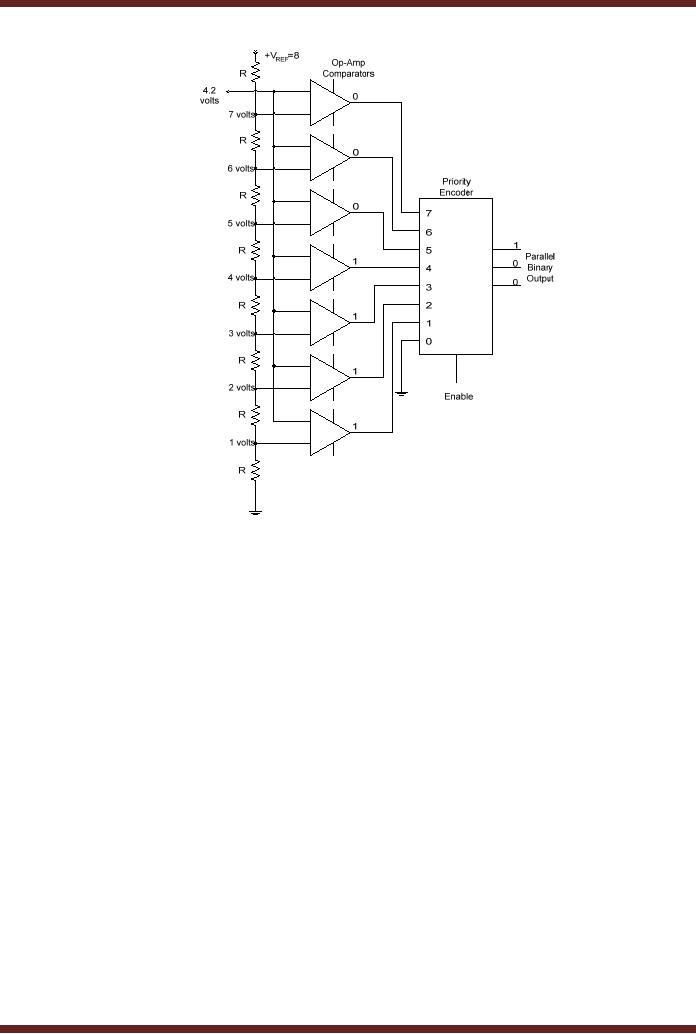
Figure 44.7a Flash A/D Converter

The analogue input sampled signal is applied at the input of the seven comparators.

The inverted input of each of the seven comparators is connected to voltage divider circuit

made up of eight resistors having the same value R. A reference voltage +VREF is connected at

the top end of the voltage divider circuit and the lower end of the voltage divider is connected

to the ground. The voltage drops across the eight resistors starting from the top most resistor

are VREF, 7/8VREF, 6/8VREF, 5/8VREF, 4/8VREF, 3/8VREF, 2/8VREF and 1/8VREF respectively. If the

input sampled voltage input is greater than the reference input voltage for any comparator, the

comparator output is logic 1, otherwise the output is logic 0. The inputs of an eight-to-three

Priority Encoder are connected to the comparator outputs. The lowest priority input of the

Encoder is grounded. The priority encoder is enabled at each sampled input and a 3-bit code

representing the value of the input sample appears at the output. Consider an example, the

input sample is 4.2 volts. The reference voltage VREF is equal to 8 volts, the seven reference

voltages applied at the inverted inputs of the seven comparators starting from the first

comparator are 7, 6, 5, 4, 3, 2 and 1 volts respectively. With an input of 4.2 volts the outputs of

the first three comparators are set to logic 0 and the outputs of the lower four comparators are

set to logic 1 which sets the encoders first three inputs to inactive-low and the next four inputs

to active high. The highest priority input the encoder outputs 100 which is binary equivalent of

4. Figure 44.7b.

448

CS302 - Digital Logic & Design

Figure 44.7b 3-bit FLASH A/D Converter

The 3-bit Flash converter requires seven comparators, a 4-bit Flash converter requires

fifteen converters. A large number of comparators are required to implement a reasonable-

sized converter. The advantage is that the conversion is done in parallel and the binary

equivalent value is available at the output of the converter almost instantaneously. Flash

converters are used for high speed conversion applications such as conversion of analogue

video signals into digital signals. For accurate reproduction of the digital signal, Flash A/D

converters are based on high number of Quantization levels which requires the use of many

Op-Amp based Comparators which makes the Flash converters expensive and power hungry

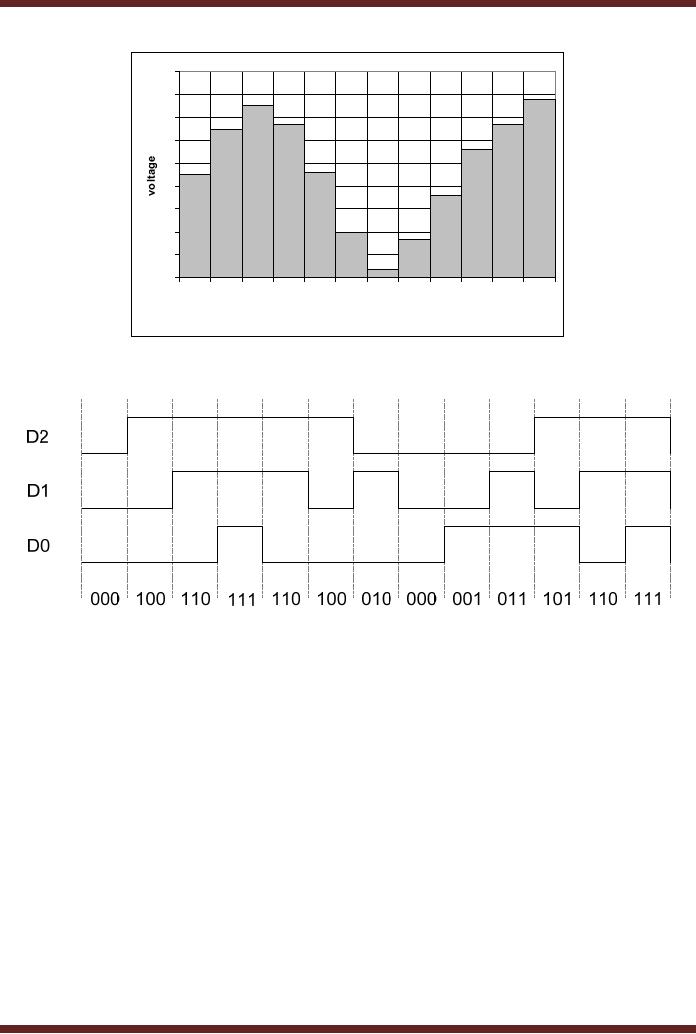
Figure 44.8 shows a set of sampled analogue voltage inputs applied at the input of the

Flash converter shown in the figure 44.7. The reference voltage of the Flash converter is set to

8 volts. At each sampling interval an enable pulse allows the Flash converter to convert the

corresponding analogue input voltage sample to be converted and represented in its binary

form. Figure 44.9.

449

CS302 - Digital Logic & Design

7.8

7.5

6.7

6.5

5.6

4.6

4.5

3.6

1.7

0.4

time

Figure 44.8

Input analogue voltage samples

Figure 44.9

Binary output representing input analogue voltage samples

Dual-Slope Analogue to Digital Converter

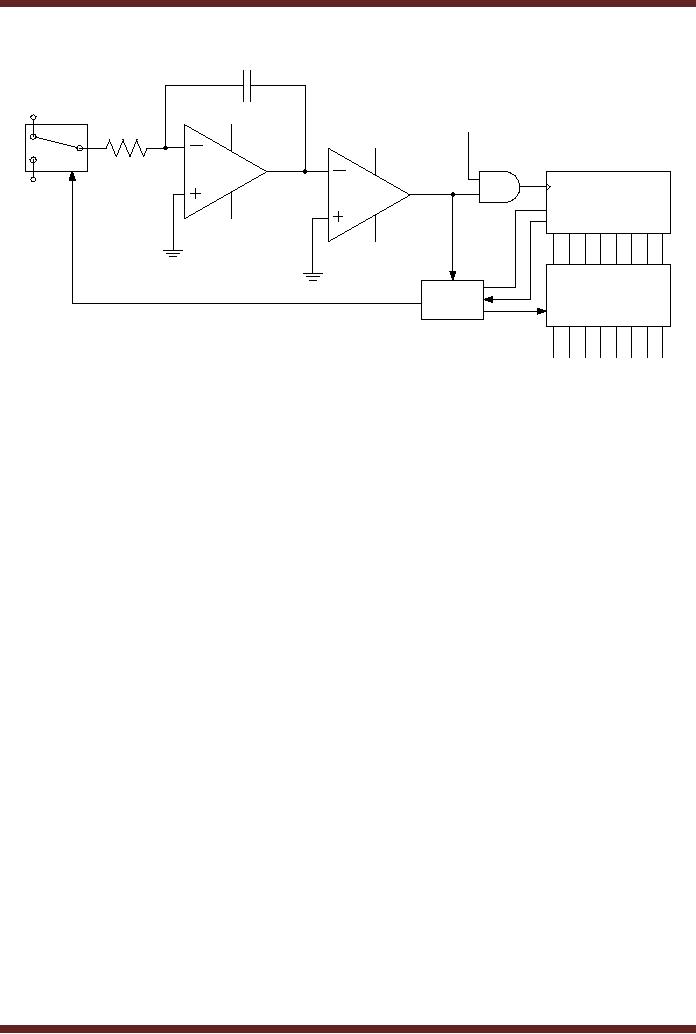
The Dual-Slope A/D converter is used in digital voltmeters and other types of

measuring instruments. A Dual-Slope A/D converter is slower than the Flash Converter. The

circuit diagram of the converter is shown. Figure 44.10. The converter consists of a switch.

Initially, the switch connects the circuit to the input analogue voltage which is to be converted

into its corresponding binary representation. During the conversion process the switch

connects the circuit to a negative reference voltage. The switching between the input voltage

and the reference voltage allows a capacitor connected between the Op-Amp output and input

to be charged and discharged. An Op-Amp based Integrator integrates the analogue input

voltage over a fixed period of time. An Op-Amp based Comparator compares the output of the

Integrator with the ground voltage to enable or disable a counter circuit. A counter and latch

counts the binary output corresponding to the analogue input value. A logic control circuit is

used to switch between analogue voltage input and the reference voltage. It also

enables/disables the latch.

450

CS302 - Digital Logic & Design

Analogue

Input (Vin)

CLK

Switch

-VREF

Counter

Integrator

CLEAR

(ramp generator)

Comparator

Control

Latches

Logic

Switch Control

Binary or BCD

Output

Figure 44.10 Dual-Slope A/D Converter

The first Op-Amp is connected as an Integrator. Initially, the counter is reset and has a

zero count. The Input switch is connected to the Analogue input which is to be converted into

equivalent binary value. The counter is reset to count zero by the Control Logic circuit. It also

sets the switch to the Analogue input voltage. The Input analogue voltage is assumed to be

constant for the duration of the conversion process. Due to the high input impedance of the

Integrator, the current from the Analogue Input source flows through the Resistor R and the

Capacitor C. The Capacitor will charge and there will be a negative-going linear voltage ramp

at the output of A1. The non-inverted input of the Comparator is connected to the ground,

therefore as the inverted input of the comparator becomes negative, the output changes to

logic 1. The Logic 1 output triggers the Control Logic which in turn resets the counter. The

logic 1 output enables the AND gate which allows the clock signal to be applied at the counter

clock input which increments the counter at each clock pulse. The Integrator output remains at

negative voltage as the negative-going linear ramp continues the integration process. As the

counter count reaches its maximum count value (terminal count), it rolls over and sends a

signal to the control Logic circuit which switches the switch to VREF. The Capacitor which is

charged to a positive input voltage discharges resulting in a positive going slope at the output

of integrator. When the voltage at the inverted input of the comparator reaches zero volt, the

comparator output become logic 0 disabling the AND gate and therefore inhibiting the counter

from counting. The Control Logic circuit sends a pulse which loads the latch with the count

value.

Table 44.2 depicts the working of the Dual-Slope A/D converter. At interval t = 0 the

converter is switched to the Vin input which is assumed to remain constant during the

conversion operation. The capacitor starts charging at a constant rate. The output of the

Integrator (voltage output) decreases at constant slope (-V). The output of the comparator is

set to 1 enabling the clock signal and incrementing the counter. The converter remains

connected to Vin for a fixed duration determined by time interval t = n. The duration of the

interval is determined by the maximum count value of the counter. During this interval the

capacitor has charged to a maximum value determined by the input voltage. At time interval t =

n, the counter reaches its terminal count and rolls over. The logic control circuit switches to

451

CS302 - Digital Logic & Design

Vref. At interval t=n+1 the capacitor begins to discharge as now it is connected to a negative

voltage -Vref . The Integrator output starts increasing towards a 0 voltage at a constant rate.

The output of the Comparator is logic high allowing the counter to count. At interval t = n+m

the capacitor has completely discharged and the comparator inputs become equal setting its

output to 0. The clock signal is disabled, disabling the counter from counting. The count value

represents the input voltage. Interval m is determined by the magnitude of the charge stored

on the capacitor. Higher the voltage stored on the capacitor longer it will take to discharge to 0

volts, thereby allowing the counter to a larger count value. If the input analogue voltage is

small, the capacitor will be charged to a smaller voltage. It will therefore discharge in a shorter

interval of time allowing the counter to count to a small value.

Time

Input

Output of

Output

Clock

Counter

interval t

signal

Integrator

Comparator

Input

Vin

-V

enabled

Counting

Vin

-V

enabled

Counting

Vin

-V

enabled

Terminal count reached.

Counter reset.

Switched to Vref

n+1

-Vref

-V

enabled

Counting

n+2

-Vref

-V

enabled

Counting

n+m

-Vref

disabled

Binary value representing

Vanalogue

Table 44.2

Operation of Dual-Slope A/D Converter

452

Table of Contents: