Octal Numbers, Octal to Binary Decimal to Octal Conversion

<< Range of Numbers and Overflow, Floating-Point, Hexadecimal Numbers

LOGIC GATES: AND Gate, OR Gate, NOT Gate, NAND Gate >>

CS302 - Digital Logic & Design

Lesson No. 04

NUMBER SYSTEMS & CODES

Octal Numbers

Octal Number system also provides a convenient way to represent long string of binary

numbers. The Octal number is a base 8 number system with digits ranging from 0 to 7. Octal

number system was prevalent in earlier digital systems and is not used in modern digital

systems especially when the Hexadecimal number is available. Each Octal Number digit can

represent a 3-bit Binary Number. The Binary Numbers and the Octal equivalents are listed in

Table 4.1

Decimal

Binary

Octal

000

001

010

011

100

101

110

111

Table 4.1

Octal Equivalents of Decimal and Binary Numbers

Counting in Octal Number System

Counting in Octal is similar to counting in any other Number system. The maximum

value represented by a single Octal digit is 7. For representing larger values a combination of

two or more Octal digits has to be used. Thus decimal 8 is represented by a combination of

108. The subscript 8 indicates the number is Octal 10 and not decimal ten. The Octal Numbers

for Decimal numbers 8 to 30 are listed in Table 4.2

Decimal

Octal

Decimal

Octal

Decimal

Octal

Table 4.2

Counting using Octal Numbers

Binary to Octal Conversion

Converting Binary to Octal is a very simple. The Binary string is divided into small

groups of 3-bits starting from the least significant bit. Each 3-bit binary group is replaced by its

Octal equivalent.

111010110101110010110

Binary Number

111 010 110 101 110 010 110 Dividing into groups of 3-bits

7 2 6 5 6 2 6

Replacing each group by its Octal equivalent

Thus 111010110101110010110 is represented in Octal by 7265626

CS302 - Digital Logic & Design

Binary strings which can not be exactly divided into a whole number of 3-bit groups are

assumed to have 0's appended in the most significant bits to complete a group.

1101100000110

Binary Number

1 101 100 000 110

Dividing into groups of 3-bits

001 101 100 000 110

Appending three 0s to complete the group

1 5 4 0 6

Replacing each group by its Octal equivalent

Octal to Binary Conversion

Converting from Octal back to binary is also very simple. Each digit of the Octal

number is replaced by an equivalent binary string of 3-bits

1726

Octal Number

001 111 010 110

Replacing each Octal digit by its 3-bit binary equivalent

Decimal to Octal Conversion

There are two methods to convert from Decimal to Octal. The first method is the

Indirect Method and the second method is the Repeated Division Method.

1. Indirect Method

A decimal number can be converted into its Octal equivalent indirectly by first

converting the decimal number into its binary equivalent and then converting the binary to

Octal.

2. Repeated Division-by-8 Method

The Repeated Division Method has been discussed earlier and used to convert

Decimal Numbers to Binary and Hexadecimal by repeatedly dividing the Decimal Number by 2

and 16 respectively. A decimal number can be directly converted into Octal by using repeated

division. The decimal number is continuously divided by 8 (base value of the Octal number

system).

The conversion of Decimal 2075 to Octal using the Repeated Division-by-8 Method is

illustrated in Table 4.3. The Octal equivalent of 207510 is 40338.

Number

Quotient after division

Remainder after division

2075

259

Table 4.3

Octal Equivalent of Decimal Numbers using Repeated Division

Octal to Decimal Conversion

Converting Octal Numbers to Decimal is done using two Methods. The first Method is

the Indirect Method and the second method is the Sum-of-Weights method.

1. Indirect Method

The indirect method of converting Octal number to decimal number is to first convert

Octal number to Binary and then Binary to Decimal.

CS302 - Digital Logic & Design

2. Sum-of-Weights Method

An Octal number can be directly converted into Decimal by using the sum of weights

method. The conversion steps using the Sum-of-Weights method are shown.

4033

Octal number

4 x 83 + 0 x 82 + 3 x 81 + 3 x 80

Writing the number in an expression

(4 x 512) + (0 x 64) + (3 x 8) + (3 x 1)

2048 + 0 + 24 + 3

Summing the Weights

2075

Decimal equivalent

Octal Addition and Subtraction

Numbers represented in Octal can be added and subtracted directly without having to

convert them into decimal or binary equivalents. The rules of Addition and Subtraction that are

used to add and subtract numbers in Decimal or Binary number systems apply to Octal

Addition and Subtraction. Octal Addition and Subtractions allows large Binary numbers to be

quickly added and subtracted.

1. Octal Addition

Carry

Number 1

Number 2

Sum

3. Octal Subtraction

Borrow

Number 1

Number 2

Difference

Working with different Binary representations

There are different ways of representing numbers in binary. Four ways of representing

binary numbers have been already discussed.

· Unsigned binary

· Signed-Magnitude form

· 2's Complement form

· Floating point notation

The different representations help in processing of numbers. For example 2's

complement based signed numbers help in handling positive and negative numbers. Floating

point notations help in handling numbers having an integer and a fraction part. Digital systems

generally allow processing of multiple data values that are of the same type. For example, one

number represented using unsigned binary can not be used to perform arithmetic operations

with another number represented using signed notation. Therefore before a digital system like

a computer is able to process data it has to be explicitly informed the types of data and the

manner in which they have been represented within the machine.

When computer Programs are written, usually as a first step of the program different

variables and their data types are declared and defined. During program execution when ever

a particular variable is accessed by the Computer it knows exactly the data type and the type

of operations that can be performed on it.

CS302 - Digital Logic & Design

Alternate forms of Binary representations

There are many different ways to represent binary numbers, other than the 4

representation that we have discussed. Many of these alternate representations are used to

support specific applications and requirements. Biased Code or Excess Code is used by

floating point numbers to represent positive and negative exponent values.

In many applications in which Digital Systems are used, the Digital systems interact

with the real world. For example, a digital controller controls a motor which positions a solar

panel to point towards the sun to extract maximum solar energy. The controller needs to

accurately know the angle at which the panel is pointing; this can be determined by the

position of the shaft of the motor with respect to some reference point. The shaft position has

to be encoded in some suitable format to be of use to the controller. A shaft encoder based on

the Gray Code is used to read the angular position of the motor shaft.

The angular position of the motor shaft can be displayed on a 7-segment display panel

in terms of Decimal Numbers. BCD Code is used to display decimal digits on 7-Segment

Display Panels.

The Excess Code

Consider the decimal number range +7 to -8. These positive and negative decimal

numbers can be represented by the 2's complement representation. The magnitude of positive

and negative numbers can not be easily compared as the positive and negative numbers

represented in 2's complement form are not represented on a uniformly increasing scale.

The decimal number range +7 to -8 is represented using an Excess-8 code that

assigns 0000 to -8 the lowest number in the range and 1111 to +7 the highest number in the

range. Excess-8 code is obtained by adding a number to the lowest number -8 in the range

such that the result is zero. The number is 8. The number 8 is added to all the remaining

decimal numbers from -7 up to the highest number +7. The Excess-8 represented is presented

in Table 4.4.

Decimal

2's

Excess-8

Decimal

2's

Excess-8

Complement

0000

1000

-8

1000

0000

0001

1001

-7

1001

0001

0010

1010

-6

1010

0010

0011

1011

-5

1011

0011

0100

1100

-4

1100

0100

0101

1101

-3

1101

0101

0110

1110

-2

1110

0110

0111

1111

-1

1111

0111

Figure 4.4

Excess-8 Code Representation of decimal numbers in the range 7 to -8

The BCD Code

Binary Coded Decimal (BCD) code is used to represent decimal digits in binary. BCD

code is a 4-bit binary code; the first 10 combinations represent the decimal digits 0 to 9. The

CS302 - Digital Logic & Design

remaining six 4-bit combinations 1010, 1011, 1100, 1101, 1110 and 1111 are considered to be

invalid and do not exist.

The BCD code representing the decimal digits 0 to 9 is shown in Table 4.4

Decimal

BCD

Decimal

BCD

0000

0101

0001

0110

0010

0111

0011

1000

0100

1001

Table 4.4

BCD representation of Decimal digits 0 to 9

To write 17, two BCD code for 1 and 7 are used 0001 and 0111. The two digits are

considered to be separate. The conventional method of representing decimal 17 using

unsigned binary is 10001. A telephone keypad having the digits 0 to 9 generates BCD codes

for the keys pressed.

Most digital systems display a count value or the time in decimal on 7-segment LED display

panels. Since the numbers displayed are in decimal, therefore the BCD Code is used to

display the decimal numbers. Consider a 2-digit 7-segment display that can display a count

value from 0 to 99. To display the two decimal digits two separate BCD codes are applied at

the two 7-segment display circuit inputs.

BCD Addition

Multi-digit BCD numbers can be added together.

0010 0011

0100 0101

0110 1000

The two 2-digit BCD numbers are added and generate a result in BCD. In the example the

least significant digits 3 and 5 add up to 8 which is a valid BCD representation. Similarly the

most significant digits 2 and 4 add up to 6 which also is a valid BCD representation.

Consider the next example where the least significant numbers add up to a number

greater than 9 for which there is no valid BCD code

0010 0011

0100 1000

0110 1011

For BCD numbers that add up to an invalid BCD number or generate a carry the number 6

(0110) is added to the invalid number. If a carry results, it is added to the next most significant

digit. Thus

CS302 - Digital Logic & Design

0011

1000

1011

11 is generated which is an invalid BCD number

0110

6 is added

1 0001

A carry is generated which is added to the result of the next most significant digits

0110

0111

The answer is 0111 0001

The Gray Code

The Gray code does not have any weights assigned to its bit positions. The Gray Code

is not a positional code. The Gray code is different from the unsigned binary code as

successive values of Gray code differ by only one bit. Table 4.5 shows the Gray Code

representation of Decimal numbers 0 to 9.

Decimal

Gray

Binary

0000

0001

0011

0010

0011

0110

0100

0111

0101

0110

0100

0111

1100

1000

1101

1001

Table 4.5

Gray Code representation of Decimal values

The bits in bold change in successive values of Gray code representation

CS302 - Digital Logic & Design

Gray Code Application

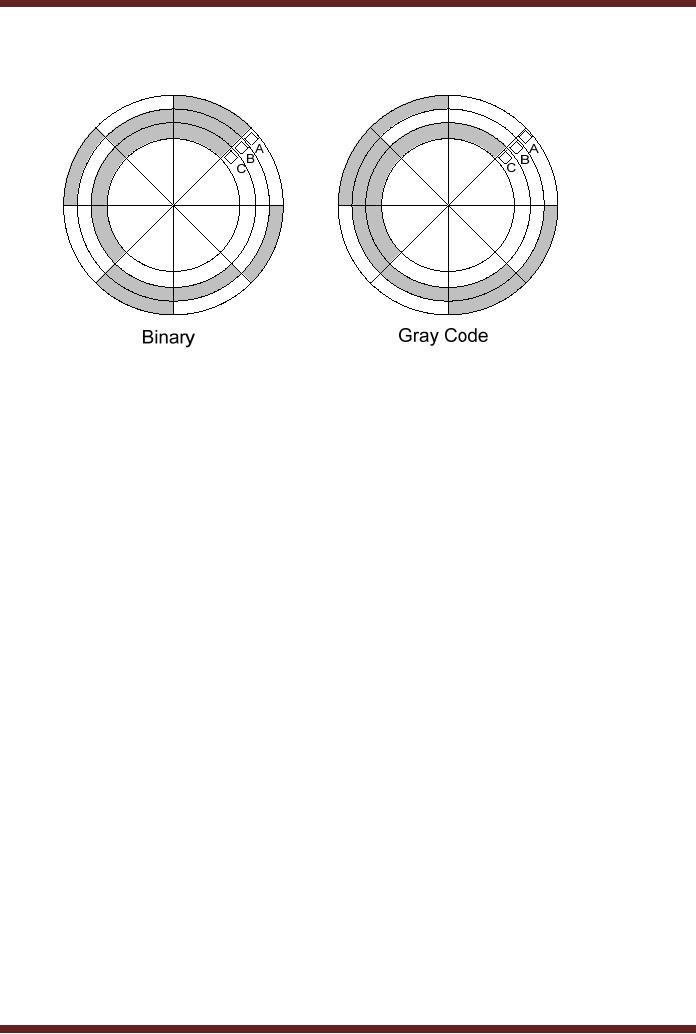
Figure 4.1

Binary and Gray Code based Shaft Encoders

The diagram shows a disk connected to the shaft of a rotating machine. The shaded

areas on the disk indicate conducting area at a voltage of +5 volts. The non-shaded areas

indicate a non-conducting area. Three stationary brushes A, B and C touch the surface of the

rotating disk. The three brushes are connected to three LED lamps through wires. As the disk

rotates the brushes come in contact with the conducting area and the insulated area. The

three LEDs display the position of the rotating shaft in terms of 3-bit numbers. Thus if the disk

on the right rotates in the anti-clockwise direction by 450 the Brush A comes in contact with the

conducting strip at 5 volts, which turns on the LED indicating Binary 001.

If the disk continuous its rotation, after a rotation of another 450, brush B comes in

contact with the conducting strip and brush A comes in contact with the non-conducting strip.

Thus LED connected to brush B lights up indicating binary 010. Thus at any instant of time, the

LEDs indicate the angular position of the rotating shaft.

Assume that the three brushes A, B and C are not aligned properly and Brush B is

slightly ahead of brushes A and C. Now if the disk rotates 900 from its start position. Brush A

would be in contact with the conducting strip, Brush B due to its misalignment would also be in

contact with the conducting strip and brush C would be in contact with the insulated strip. Thus

when the disk rotates the LEDs will show a 001, followed by a 011 for a short duration when

the disk rotates from 900 to 910 and then to 010. Thus due to misalignment the count value

jumped from 1 to 3 and then back to 2.

Consider the disk shown on the right. The conducting and non-conducting strips follow

a Gray Code pattern 000, 001, 011, 010, 110, 111, 101 and 100 representing decimal 0, 1, 2,

3, 4, 5, 6 and 7. Now even if the brushes are misaligned, the LEDs would always display the

correct count value. Thus a Gray Code based shaft encoder allows angular position of the

shaft to be determined even when the brushes are misaligned.

Alphanumeric Codes

All the representation studied so far allow decimal numbers to be represented in

binary. Digital systems also process text information as in editing of documents. Thus each

letter of the alphabet, upper case and lower case, along with the punctuation marks should

CS302 - Digital Logic & Design

have a representation. Numbers are also written in textual form such as 2nd June 2003. The

ASCII Code is a universally accepted code that allows 128 characters and symbols to be

represented.

ASCII Code

The ASCII Code (American Standard Code for Information Interchange) is a 7-bit code

representing 128 unique codes which represent the alphabet characters A to Z in lower case

and upper case, the decimal numbers 0 to 9, punctuation marks and control characters.

ASCII codes 011 0000 (30h) to 011 1001 (39h) represents numbers 0 to 9

ASCII codes 110 0001 (61h) to 111 1010 (7Ah) represent lower case alphabets a to z

ASCII codes 100 0001 (41h) to 101 1010 (5Ah) represent upper case alphabets A to Z

ASCII codes 000 0000 (0h) to 001 1111 (1Fh) represent the 32 Control characters.

Extended ASCII Code

The 7-bit ASCII code only has 128 unique codes which are not enough to represent

some graphical characters displayed on Computer screens. An 8-bit code Extended ASCII

code gives 256 unique codes. The extended 128 unique codes represent graphic symbols

which have become an unofficial standard as vendors use their own interpretation of these

graphic codes.

Parity Method

Binary information which can be text or numbers is processed, stored and transmitted.

Although digital systems are extremely reliable but still there is a possibility that one bit gets

corrupted. That is, a 1 changes to 0 or 0 changes to 1. Many systems use a parity bit to detect

errors. A single parity based error detection scheme is not very practically efficient and more

elaborate and robust schemes have been designed and implemented to detect and correct

multiple bit errors. However, the use of a parity bit does help in understanding the basic

concept of error detection.

Consider that the 8-bit Extended ASCII Code is used to transmit text messages from

one location to another remote location. An extra bit is appended with the 8 data bits making a

total of nine bits. The 8-bits comprise the information that is to be stored or transmitted and the

extra parity bit is appended to check for any errors that might occur during the storage or

transmission of the information. Two schemes are used, Even Parity or Odd Parity essentially

the two schemes are identical except for a very minor difference.

Even Parity Method

The information 10001101 is to be transmitted to a remote location. A parity bit error

detection method is adopted to indicate if the information has been corrupted when it reaches

the other end. In the Even Parity method the number of 1s is counted in the information and

depending upon the number of 1s in the message the appended parity bit is either set to 0 or 1

to make the total number of 1s to be even (Even Parity)

The 8-bit data 10001101 has even number of 1s, therefore the parity bit which is

appended is set to 0. The 9-bit message is 100011010. The parity bit is indicated in Bold.

Suppose the message received at the other end of the wire shows the bits to be 101011010,

the underlined bit has changed from 0 to1. Before transmitting the message, the users at both

ends of the wire have agreed that they would be sending and receiving messages using even

CS302 - Digital Logic & Design

parity. Thus the receiver on receiving the 9-bit message does a quick parity check. The total

number of bits including the parity bit should add up to an even number. However, in this case

the numbers of 1 in the message add up to 5 which indicates that a bit has been corrupted.

There is no way that the receiver can know the location of the corrupted bit in the message.

The only solution is to request the sender to retransmit the message. If two bits get corrupted

during the transmission, 101001010 then the total number of 1s remains the same and the

receiver would not be able to detect an error. If 3-bits get corrupted, 101000010 the user

would still be able to detect that an error has occurred, however there is no way to determine if

a single bit or 3-bit, or 5-bit or 7-bit error has occurred.

Odd parity is identical except that both the sender and receiver agree to send

information using the Odd parity and the parity bit is set or cleared so that the total number of

1s in the message including the Parity bit sums up to an Odd Number.

Table of Contents: