NEXT-STATE TABLE: Flip-flop Transition Table, Karnaugh Maps

<< DIGITAL CLOCK: Clocked Synchronous State Machines

D FLIP-FLOP BASED IMPLEMENTATION >>

CS302 - Digital Logic & Design

Lesson No. 31

2. NEXT-STATE TABLE

Once the state diagram of the sequential circuit is defined, a Next-State Table is

derived which lists each present state and the corresponding next state. The next state is the

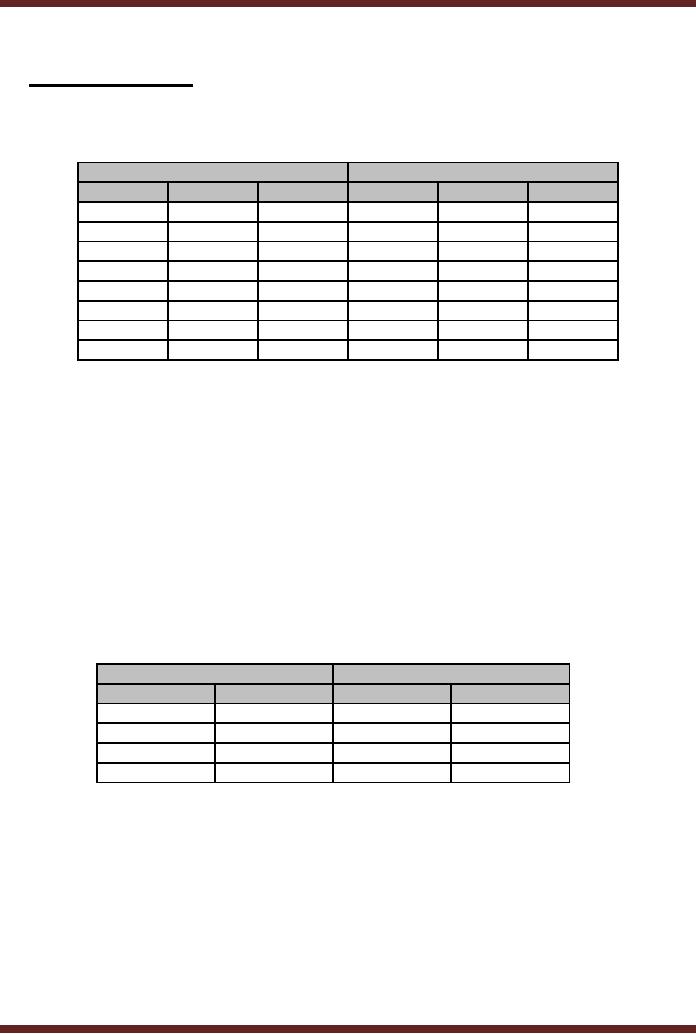
state to which the sequential circuit switches when a clock transition occurs. Table 31.1

Present State

Next State

Table 31.1

Next-State Table for a 3-bit Up-Counter

3. Flip-flop Transition Table

The Memory element of the Sequential circuit is implemented using flip-flops. The

number of flip-flops used is determined by the total number of states. When there is a clock

transition at the clock input of the flip-flops they change from their present state to the next

state. The Flip-flop transition table lists all the possible flip-flop input combinations which allow

the present state to change to the next state on a clock transition. The flip-flop transition table

is based on the flip-flop used (D, S-R or J-K). Table 31.2. In the transition table the present

state logic 0 changes to next state logic 0, when J-K inputs are 0 and 0 respectively or J-K

inputs are 0 and 1 respectively. Thus if input J=0 the next state output is 0. Similarly when J-K

inputs are 1 and 1 or 1 and 0 the next state output is set to logic 1. Thus if input J=1 the next

state output is 1. Similarly for the other two transition cases K=1 and K=0 sets the next state

output to logic 0 and 1 respectively.

Flip-flop Inputs

Output Transitions

Qt+1

Table 31.2

J-K flip-flop Transition table

4. Karnaugh Maps

For each state variable shown in the Next-State table, the change from present state to

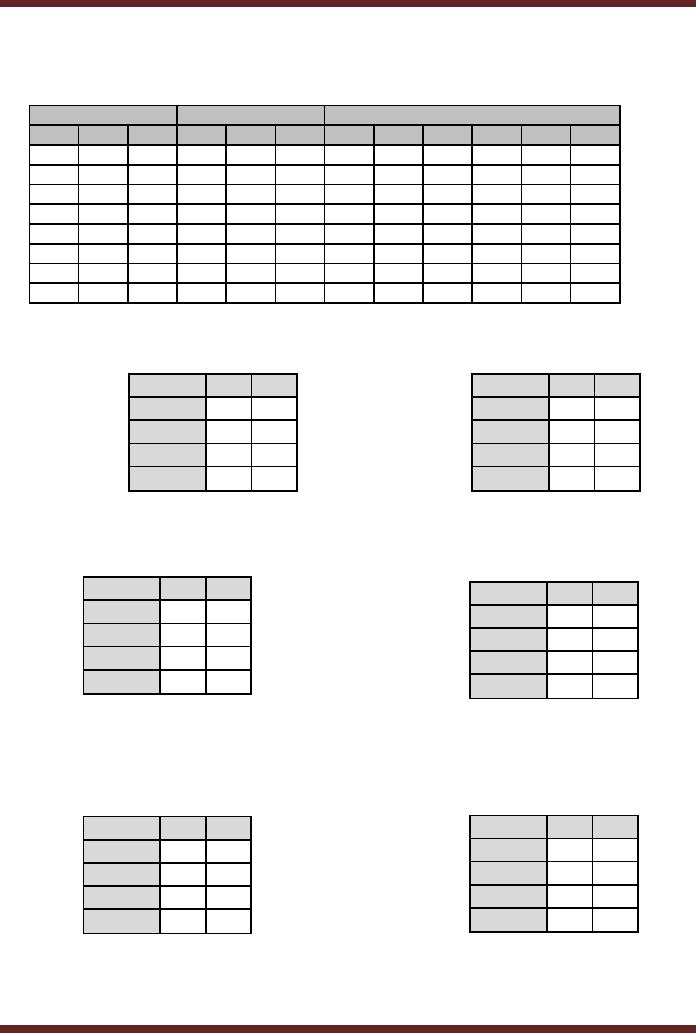
the next state on a clock transition depends upon the J-K inputs. Table 31.3. Considering the

state variable Q2, J2 and K2 inputs set to 0 and x (don't care) allow Q2 to change from present

state 0 to next state 0. Similarly, the state variable Q0 changes from 1 to 0 when J0 and K0

inputs are set at x (don't care) and 1 respectively. The table is completed using the information

321

CS302 - Digital Logic & Design

in the Next-State table and the J-K flip-flop transition table. The J-K inputs can be directly

mapped to Karnaugh maps. Table 31.4

Present State

Next State

J-K flip-flop inputs

Table 31.3

J-K flip-flop input table

Q2Q1/Q0

J2 = Q1Q 0

K 2 = Q1Q 0

Table 31.4a

Karnaugh Map for J2 and K2 inputs

Q2Q1/Q0

J1 = Q 0

K1 = Q0

Table 31.4b

Karnaugh Map for J1 and K1 inputs

Q2Q1/Q0

J0 = 1

K0 = 1

Table 31.4c

Karnaugh Map for J0 and K0 inputs

322

CS302 - Digital Logic & Design

5. Logic expressions for Flip-flop Inputs

Simplified expressions for J2-K2, J1-K1 and J0-K0 are directly obtained from the

Karnaugh maps. The expressions are shown along with the Karnaugh maps.

6. Sequential Circuit Implementation

The Boolean expressions obtained in the previous step are implemented using logic

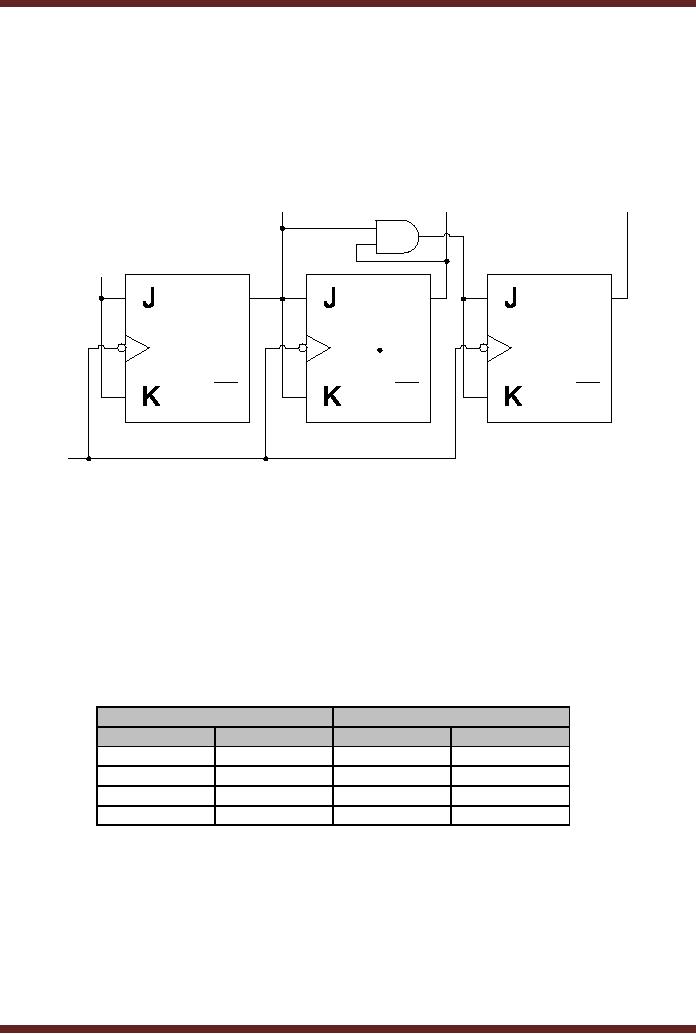
gates. The sequential circuit implemented is shown in figure 30.8.

SET

flip-flop 1

flip-flop 2

flip-flop 3

CLR

CLK

Figure 31.1

Implementation of the Sequential Circuit

The 3-bit up counter can be implemented using S-R flip-flops and D flip-flops.

Implementation of the counter using S-R flip-flop requires the use of S-R flip-flop transition

table in step 3. The remaining steps follow step 3.

S-R flip-flop based Implementation

Flip-Flop Transition Table

To implement the counter using S-R flip-flops instead of J-K flip-flops, the S-R

transition table is used. The S-R flip-flop does not allow S and R inputs to be set to logic 1 and

1 respectively and is considered to be an invalid state. Based on the three set of valid inputs

the S-R transition table is shown. Table 31.5

Flip-flop Inputs

Output Transitions

Qt+1

Table 31.5

S-R flip-flop Transition table

Karnaugh Maps

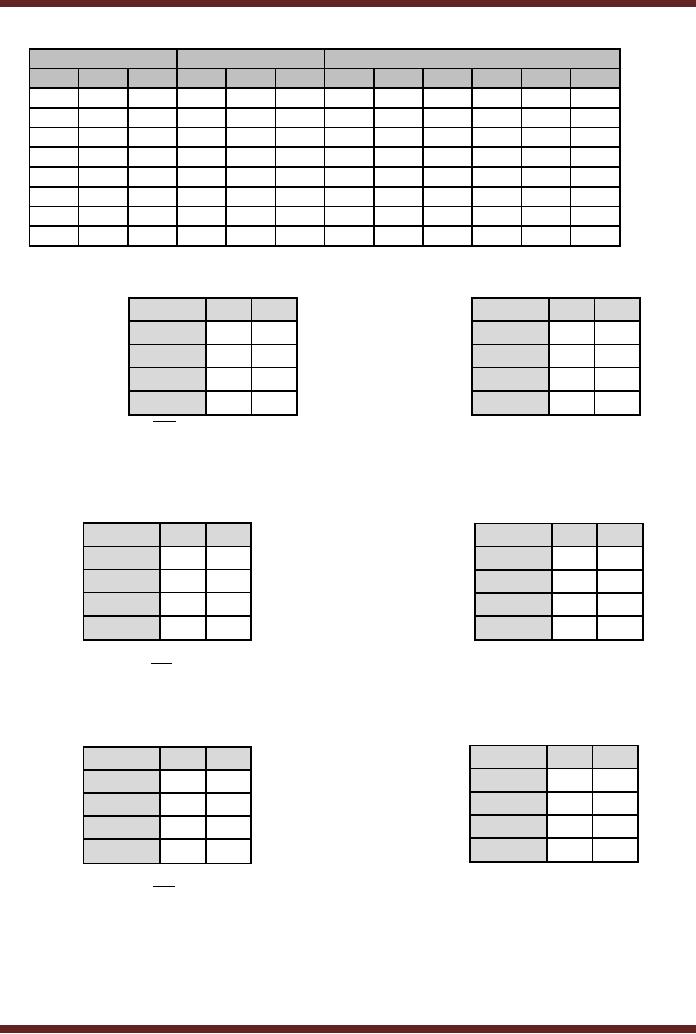
The S-R input table is shown in table 31.6. The Karnaugh maps for the input

expressions are also derived from the input table.

323

CS302 - Digital Logic & Design

Present State

Next State

S-R flip-flop inputs

Table 31.6

S-R flip-flop input table

Q2Q1/Q0

S 2 = Q 2Q1Q 0

R 2 = Q 2Q1Q 0

Table 31.7a

Karnaugh Map for S2 and R2 inputs

Q2Q1/Q0

R1 = Q1Q 0

S1 = Q1Q 0

Table 31.7b

Karnaugh Map for S1 and R1 inputs

Q2Q1/Q0

S0 = Q0

R0 = Q0

Karnaugh Map for S0 and R0 inputs

Table 31.7c

Logic expressions for Flip-flop Inputs

324

CS302 - Digital Logic & Design

Simplified expressions for S2-R2, S1-R1 and S0-R0 are directly obtained from the

Karnaugh maps. The expressions are shown along with the Karnaugh maps.

Sequential Circuit Implementation

The implementation of the 3-bit synchronous counter based on S-R flip-flops is shown.

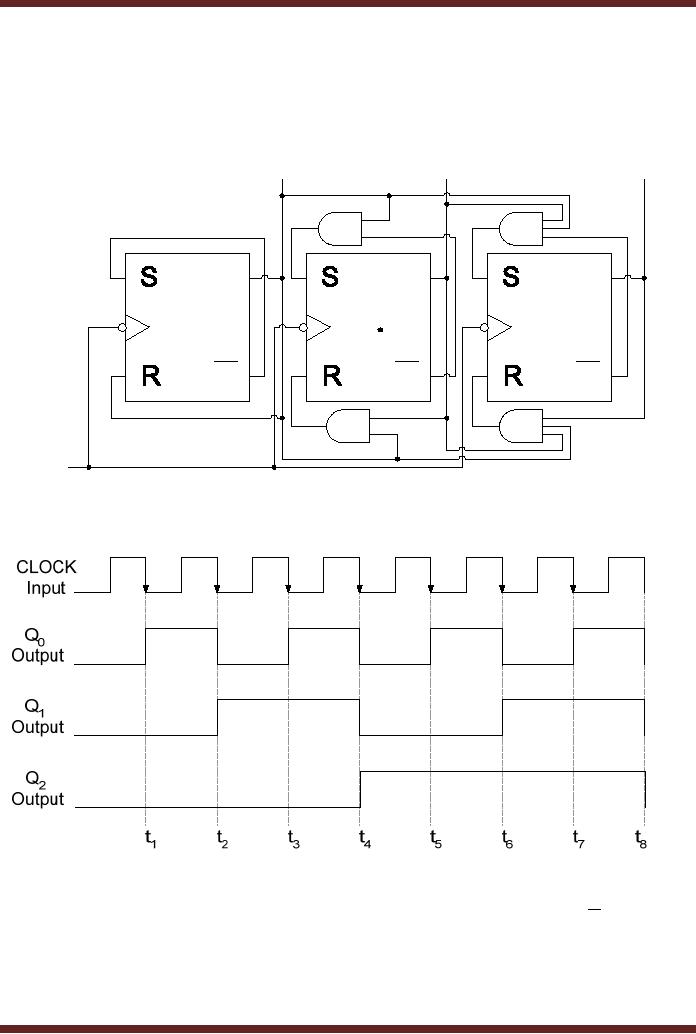
Figure 31.2

SET

flip-flop 1

flip-flop 2

flip-flop 3

CLR

CLK

Figure 31.2a S-R flip-flop based implementation of 3-bit Synchronous Counter

Figure 31.2b Timing diagram of the S-R flip-flop based 3-bit Synchronous Counter

The S-R inputs of the first flip-flop are cross connected to its Q and Q outputs. At

interval t1 the Q0 output is at logic 0, the R input is at logic 0 and S input is at logic 1, thus the

flip-flop is set to logic 1. When the Q0 output is at logic 1, the S and R inputs are at logic 0 and

1 respectively, thus at t2 the clock transition the flip-flop is reset to 0. At t1 the S and R inputs of

the second-flip-flop are at logic 0 as Q0 is at logic 0, thus at the clock transition the output of

325

CS302 - Digital Logic & Design

the second flip-flop remains unchanged. At interval t2, the S and R inputs of the second flip-

flop are set to 1 and 0 respectively, thus it is set to logic 1 on the clock transition. Similarly, at

interval t4 the S-R inputs of the third flip-flop are set to logic 1 and 0 respectively, the flip-flop is

set to logic 1 on the clock transition.

326

Table of Contents: