Down Counter with truncated sequence, 4-bit Synchronous Decade Counter

<< THE 555 TIMER: Race Conditions, Asynchronous, Ripple Counters

Mod-n Synchronous Counter, Cascading Counters, Up-Down Counter >>

CS302 - Digital Logic & Design

Lesson No. 27

DOWN COUNTERS

All the examples considered so far have used counters that count up from binary zero

to some maximum count value depending upon the Modulus value of the counter. When the

counter reaches its maximum count value it is reset to binary zero and continues with the

counting sequence. A down counter counts in a sequence which starts with some maximum

count value and counts down to binary zero. It is then reset to the maximum count value and

repeats the counting sequence. A Down-counter is implemented by connecting the Q output

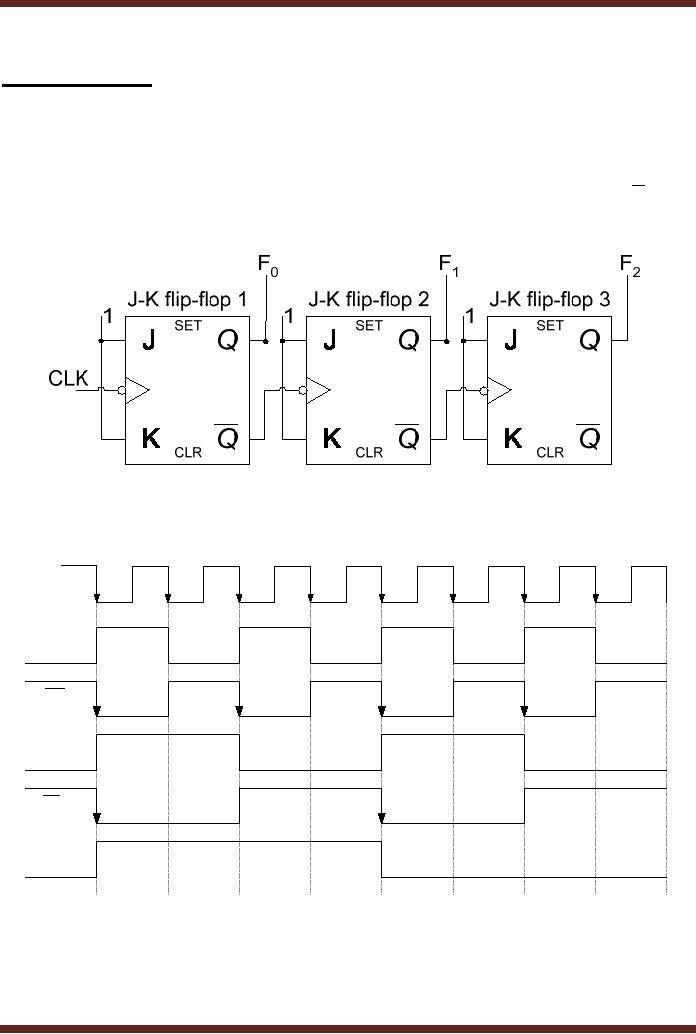
instead of the Q output of all the flip-flops to the clock inputs of the next flip-flops. Figure 27.1

Figure 27.1a 3-bit Asynchronous Down-Counter

CLOCK

Input

Figure 27.1b Timing diagram of a 3-bit Asynchronous Down-Counter

277

CS302 - Digital Logic & Design

Down Counter with truncated sequence

A down counter can be configured to count down a truncated sequence, similar to an

up-counter which can count up to any truncated sequence. A down counter counts down from

the maximum count value to some predefined count value which is the last count value in the

truncated sequence. On reaching the last count value the down-counter is preset to the

maximum count value instead of clearing the counter to zero count value as done in the case

of an up-counter. The circuit shows a 3-bit down-counter configured to count down a truncated

sequence from 111 to 011. On reaching the count value 011, the counter is preset to 111

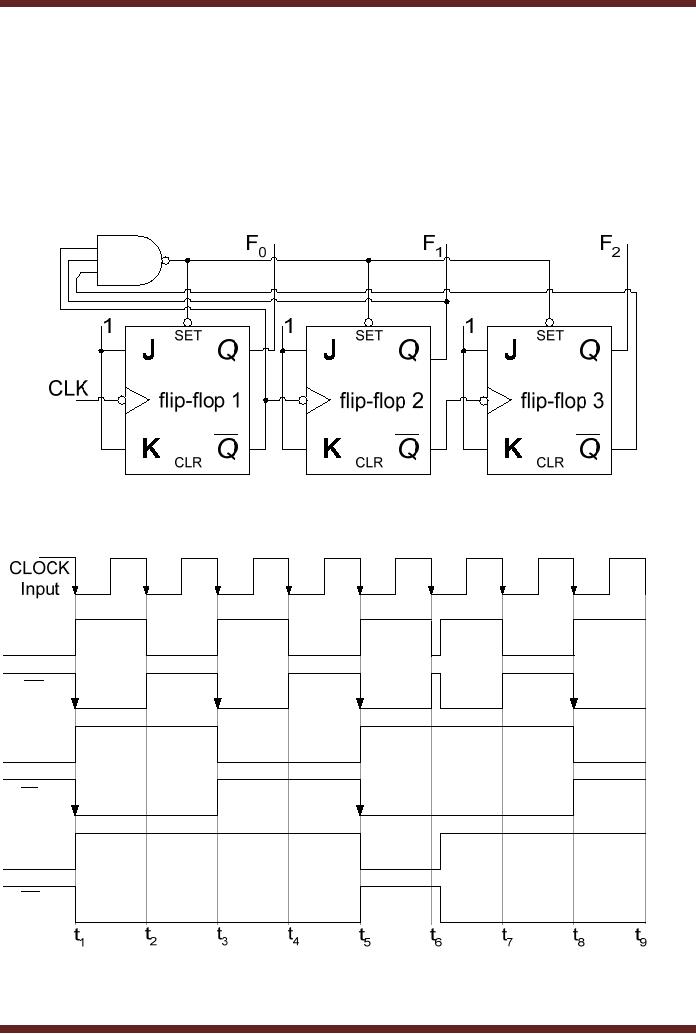
when it is decremented to 010 on the negative clock transition. Figure 27.2

Figure 27.2a Down-counter configured to count a truncated sequence

Figure 27.2b Timing diagram of a counter configured to count a truncated sequence

278

CS302 - Digital Logic & Design

The counter counts down from 111 to 011 from interval t1 to interval t5. At interval t6 the

counter counts down to 010, the F0 , F1 and F2 are set to logic 1, the output of the NAND gate

is set to logic 0 which presets all the three flip-flops to state 111. The counter continues with its

counting sequence and at the clock transition at interval t7 and t8 the counter count down to

110 and 101 respectively.

Synchronous Counters

Asynchronous counters due to the delayed outputs caused by the rippling clock signal

do not allow their operation with high frequency clock signals. Asynchronous counters having

multiple bits also cause timing problems due to the excessive propagation delays.

Applications requiring 8, 16 and 32 counters and operating at high clock frequencies

are implemented using Synchronous Counters. Synchronous counters use a common clock

signal connected to the clock inputs of all the counter flip-flops. Therefore, on a clock transition

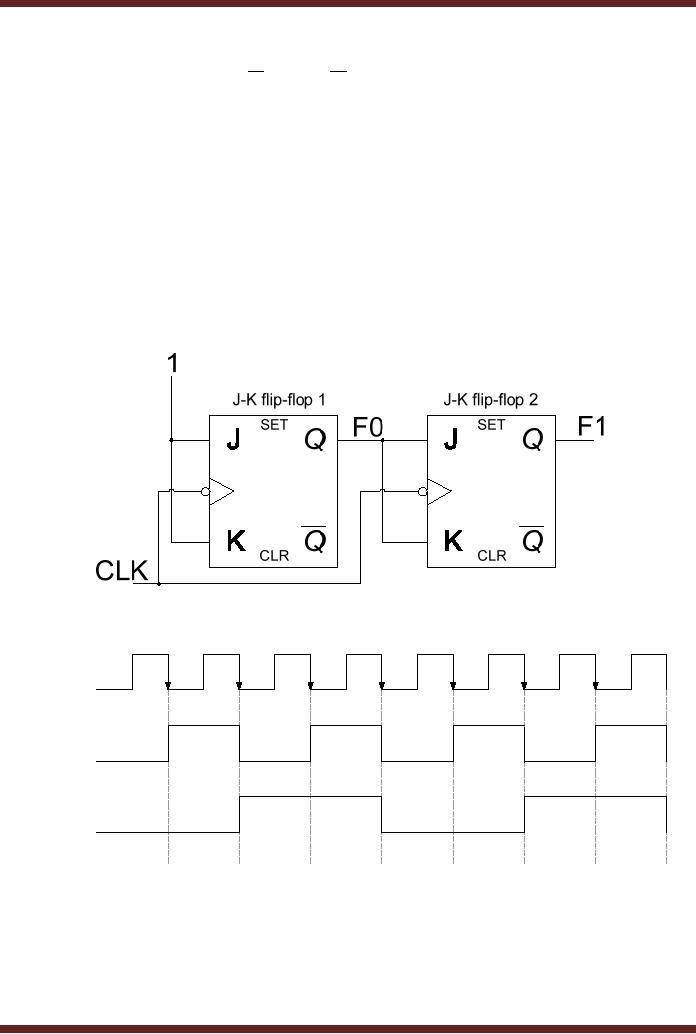
all the flip-flops simultaneously change their output state. Figure 27.3.

Figure 27.3a 2-bit Synchronous Counter

CLOCK

Input

Output

Figure 27.3b Timing diagram of a 2-bit Synchronous Counter

The 2-bit Synchronous counter has both its clock inputs connected to the clock signal.

Both the flip-flops are reset to logic low states respectively. On a high to low clock transition at

interval t1, the F0 output of the first flip-flop toggles to logic high. Since the clock transition on

279

CS302 - Digital Logic & Design

the clock input of the second flip-flop also occurs at interval t1, the J-K inputs of the second flip-

flop are at interval t1 are at logic 0. The change at the inputs J-K to logic 1 of the second flip-

flop occurs after a propagation delay tPLH of the first flip-flop. Thus the output of the second flip-

flop remains unchanged due to the input condition at the J-K inputs (J=0, K=0). At interval t2

the output F0 is at logic high (1) along with the J-K inputs as the three are connected together.

On a clock transition at interval t2 the output F0 toggles to logic 0. At the very same instant the

output F1 also toggles to logic 1. The inputs J-K of the second flip-flop is set to logic 0 after a

propagation delay of tPHL of the first flip-flop. At interval t3, at the clock transition the output F0

toggles to logic 1. The inputs J-K of the second flip-flop at time interval t3 is logic 0 therefore at

the clock transition the output F1 remains unchanged. The inputs J-K of the second flip-flop

change after a propagation delay of tPLH. Finally, at time interval t4, the output F0 of the first flip-

flop toggles to logic 0. The J-K inputs of the second flip-flop are at logic 1, therefore the output

F1 of the second flip-flop is also set to logic 0.

3-bit & 4-bit Synchronous Counters

Multi-bit Synchronous Counters can easily be implemented by connecting together

appropriate number of flip-flops together. The clock inputs of all the flip-flops are directly

connected to a common clock signal. Implementing of Synchronous Counters larger than 2-

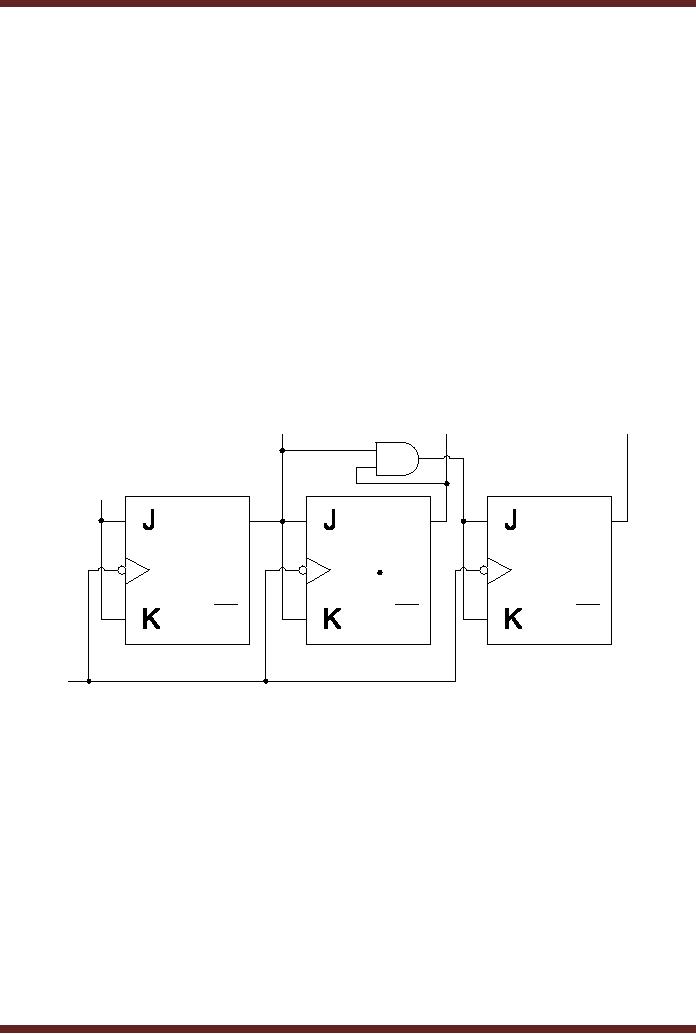
bits requires the use of an AND gate. Figure 27.4

SET

flip-flop 1

flip-flop 2

flip-flop 3

CLR

CLK

Figure 27.4a

A 3-bit Synchronous Counter

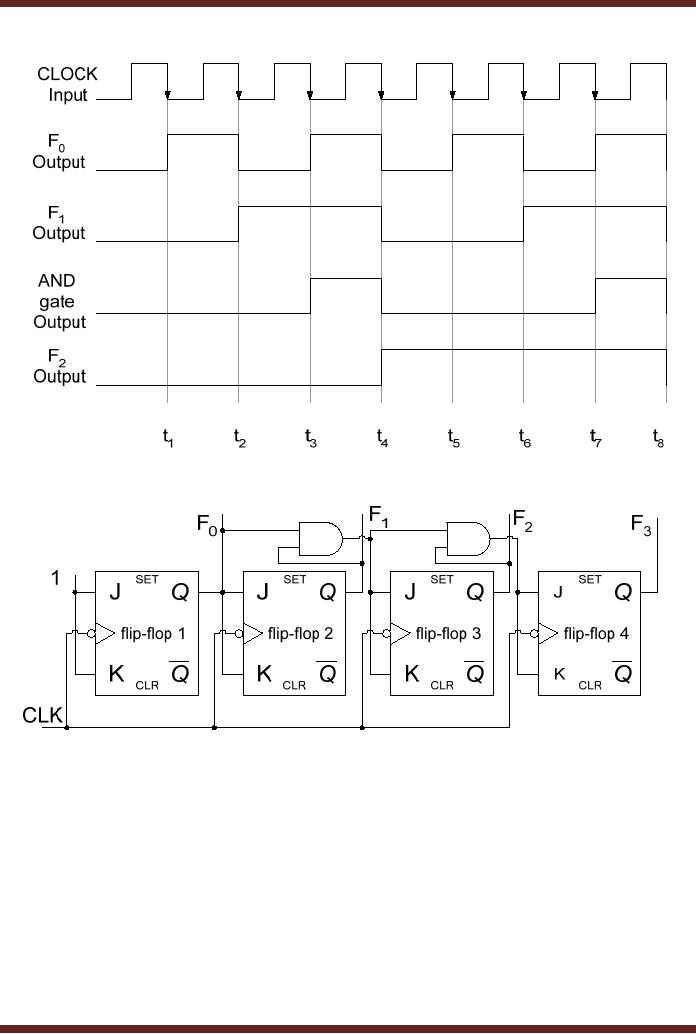
The operation of the 3-bit Synchronous Counter and the need for the AND gate can be

understood by studying the timing diagram of the 3-bit counter. The timing of the first two flip-

flops is identical to the timings of the 2-bit counter discussed earlier. The timing diagram

shows that at interval t4, the 3-bit counter should count from state 011 to 100. Similarly, at

interval t8 the counter should count from state 111 to 000. At both the intervals the F2 output of

the third flip-flop toggles to logic 1 and logic 0 respectively when the outputs F0 and F1 are both

at logic 1. This is implemented by connecting the two outputs F0 and F1 to the inputs of a 2-

input AND gate. The output of the AND gate is logic 1 when both its inputs (F0 and F1) are at

logic 1. The output of the AND gate is connect to the J-K inputs of the third flip-flop. If the AND

gate is not used and the J-K inputs of the third flip-flop are directly connected to the output F1

of the second flip-flop, the third flip-flop will change its state and set its output F2 to logic 1 at

the time interval t3. The count sequence is thus disturbed.

280

CS302 - Digital Logic & Design

Figure 27.4b

Timing diagram of a 3-bit Synchronous Counter

Figure 27.5

4-bit Synchronous Binary Counter

Larger counters can be implemented using similar AND gates. For example, a 4-bit

counter uses four flip-flops. The counter circuit for the first three flip-flops is identical to the 3-

bit counter circuit. The input of the fourth flip-flop is connected through a 3-input AND gate with

inputs F0, F1 and F2. The fourth flip-flop changes its state when the outputs of the first three

flip-flops are at logic 1. That is, the when the 4-bit counter is counting from 0111 to 1000 and

1111 to 0000. Figure 27.5

4-bit Synchronous Decade Counter

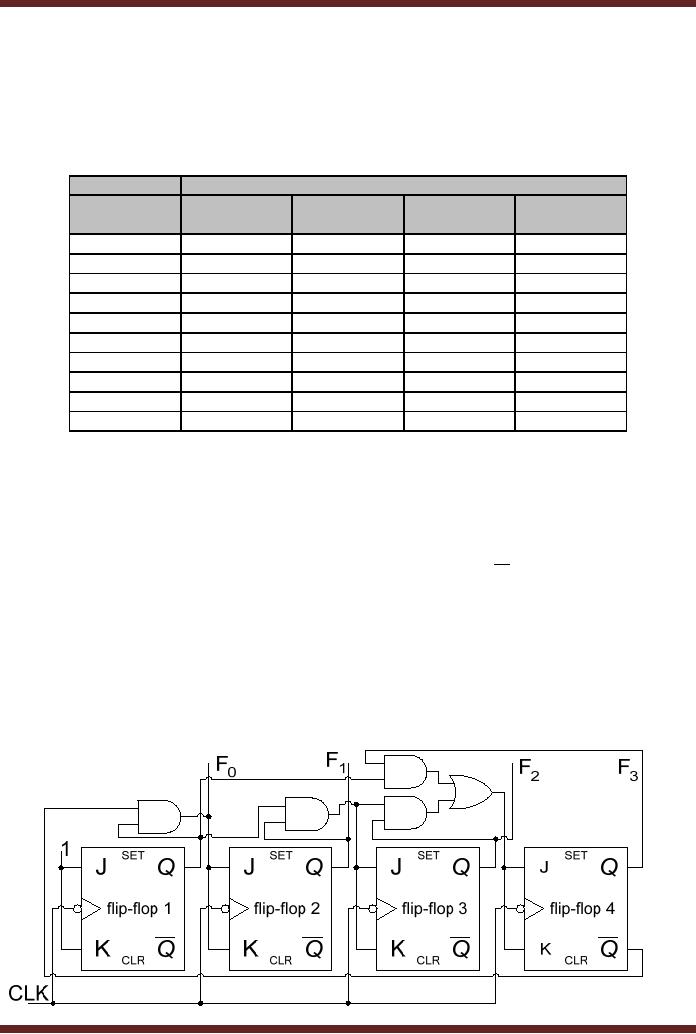
Earlier, an Asynchronous Decade counter has been discussed, which counts from

state 0000 to 1001. The Asynchronous counter is cleared to state 0000 when the counter

counts from 1001 to 1010. Synchronous counter can be implemented which counts from 0000

to 1001. In the synchronous counter, all the four flip-flops are connected to a common clock

281

CS302 - Digital Logic & Design

and are triggered simultaneously. However, instead of using the clear asynchronous inputs to

clear the counter to the initial state, logic gates are used to reset the decade counter to state

0000 after it reaches state 1001. The implementation of the Synchronous Decade counter can

be understood with the help of a function table that represents the operation of the Decade

Counter. Table 27.1.

Input

Output

Clock

Pulses

Table 27.1

Output of a Synchronous Decade Counter

The output state of the first flip-flop F0 is shown to toggle between 1 and 0 on each

clock transition. Therefore, the inputs J-K of the first flip-flop are connected to logic high. The

output state of the second flip-flop F1 changes from logic 0 to logic 1 and vice- verse when F0

output is logic 1 and F3 output is logic 0. Therefore, the inputs J-K of the second flip-flop are

connected to a function determined by the Boolean expression F0 F3 . The output state of the

third flip-flop F2 changes from logic 0 to logic 1 and vice-versa when F0 and F1 outputs are both

at logic 1. Therefore, the inputs J-K of the third flip-flop are connected to a function determined

by the Boolean expression F0F1 . The output of the fourth flip-flop F3 changes its output state

when outputs F0, F1 and F2 are at logic 1 or when outputs F0 and F3 are at logic 1. Therefore,

the J-K inputs of the fourth flip-flop are connected to a function determined by a Boolean

expression F0F1F2 + F0F3 . The decade counter is shown in figure 27.6

282

CS302 - Digital Logic & Design

Figure 27.6

Synchronous Decade Counter

283

Table of Contents: