Dual Positive-Edge triggered D flip-flop, J-K flip-flop, Master-Slave Flip-Flops

<< Data Storage using D-flip-flop, Synchronizing Asynchronous inputs using D flip-flop

THE 555 TIMER: Race Conditions, Asynchronous, Ripple Counters >>

CS302 - Digital Logic & Design

Lesson No. 25

ASYNCHRONOUS PRESET AND CLEAR INPUTS

The S-R, J-K and D inputs are known as synchronous inputs because the outputs

change when appropriate input values are applied at the inputs and a clock signal is applied at

the clock input. If there is no clock transition then the inputs have no effect on the output.

Digital circuits require that the flip-flops be set or reset to some initial state before a new set of

inputs is applied for changing the output. The flip-flops are set-reset to some initial state by

using asynchronous inputs known as Preset and Clear inputs. Since these inputs change the

output to a known logic level independently of the clock signal therefore these inputs are

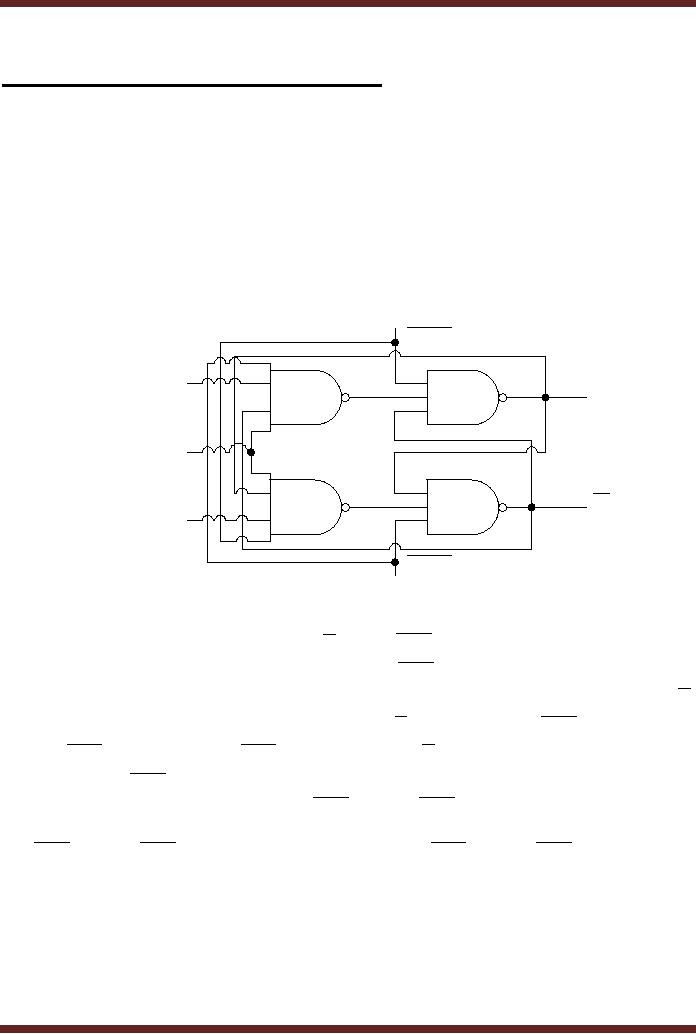
known as asynchronous inputs. The circuit diagram of a J-K flip-flop with Preset and Set

Asynchronous inputs is shown in figure 25.1a. The asynchronous inputs override the

synchronous inputs thus to operate the flip-flop in the synchronous mode the asynchronous

inputs have to be disabled.

PRE

CLK

CLR

Figure 25.1a J-K flip-flop with Asynchronous Preset and Clear inputs

To preset the flip-flop to Q=1 and Q =0 the PRE input is set to 0 which sets the Q

output to 1 and the output of NAND gate 4 to 1. The CLR input is set to 1, the remaining two

inputs (Q and output of NAND gate 4) of the NAND gate 2 are also set at logic 1, therefore Q

output is set to 0. The flip-flop is cleared to Q=0 and Q =1 by setting the PRE input is set to 1

and the CLR input is to 0. The CLR input set to 0 sets Q =1 it also sets the output of NAND

gate 3 to 1. The PRE input along with the other two inputs of NAND gate 1 are set at logic 1

which sets the output Q to 0. When the PRE and the CLR inputs are used inputs J and K

have no effect on the operation of the flip-flop. To use the flip-flop with synchronous inputs J-K,

the PRE and the CLR inputs are set to logic 1. Setting PRE and the CLR to logic 0 is not

allowed.

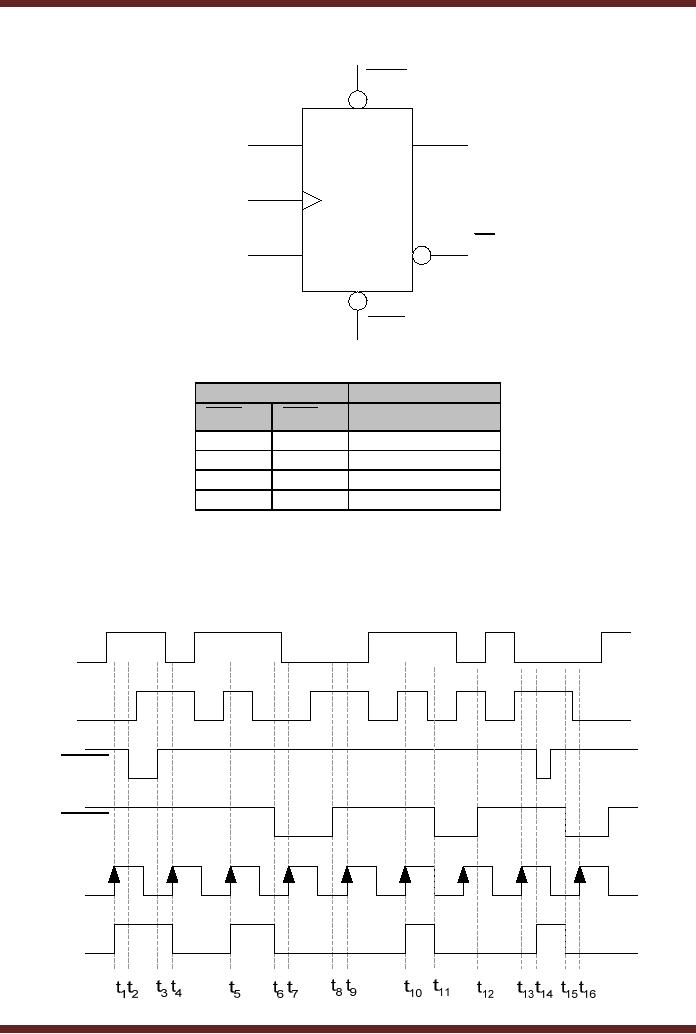
Logic symbol of a J-K edge-triggered flip-flop with synchronous and asynchronous

inputs is shown in figure 25.1b. The truth table of a J-K flip-flop with Asynchronous inputs is

shown in table 25.1. The timing diagram describes the effect of asynchronous inputs on the

operation of the flip-flop. Figure 25.1c

255

CS302 - Digital Logic & Design

PRE

J-K

CLK

Flip-Flop

CLR

Figure 25.1b Logic Symbol of a J-K flip-flop with Asynchronous inputs

Input

Output

Qt+1

CLR

PRE

Invalid

Clocked operation

Table 25.1

Truth table of J-K flip-flop with Asynchronous inputs

PRE

CLR

CLK

Figure 25.1c Timing diagram of a J-K flip-flop with Preset and Clear inputs

256

CS302 - Digital Logic & Design

The 74HC74 Dual Positive-Edge triggered D flip-flop

The edge-triggered D flip-flop with asynchronous inputs is available as an Integrated

Circuit. The 74HC74 has dual D-flip-flops with independent clock inputs, synchronous and

asynchronous inputs.

The 74HC112 Dual Positive-Edge triggered J-K flip-flop

The edge-triggered D flip-flop with asynchronous inputs is available as an Integrated

Circuit. The 74HC112 has dual J-K-flip-flops with independent clock inputs, synchronous and

asynchronous inputs.

Master-Slave Flip-Flops

Master-Slave flip-flops have become obsolete and are replaced by edge-triggered flip-

flops. Master-Slave flips have two stages each stage works in one half of the clock signal. The

inputs are applied in the first half of the clock signal. The outputs do not change until the

second half of the clock signal. As mentioned earlier the use of edge-triggered flip-flip is to

synchronize the operation of a digital circuit with a common clock signal. The master-slave

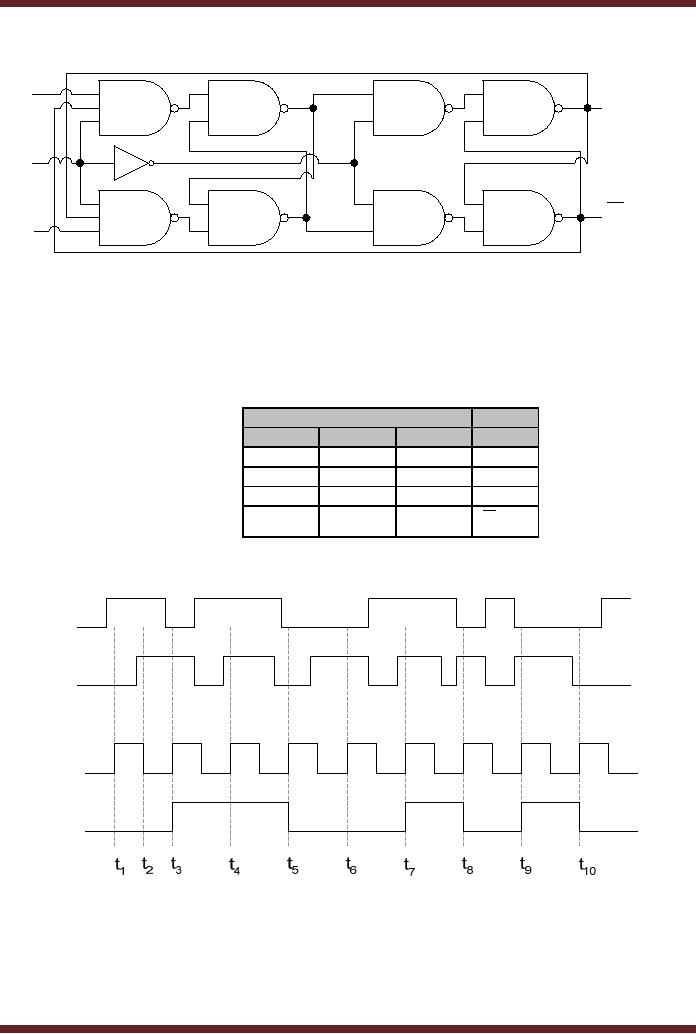
setup also allows digital circuits to operate in synchronization with a common clock signal. The

circuit diagram of the master-slave J-K flip-flop is shown in figure 25.2a. The Master-Slave flip-

flop is composed of two parts the Master and the Slave. Both the Master and the Slave are

Gated S-R flip-flops. The Master-Slave flip-flop is not synchronised with the clock positive or

negative transition, rather it known as a pulse triggered flip-flop as it operates at the positive

and negative clock cycles.

Consider that the J-K inputs of the flip-flop are set at 1 and 0 respectively. The outputs

Q and Q are initially set at 1 and 0 respectively. During the positive half of the clock gates 3

and 4 are both enabled by the clock signal. The output of gate 3 is set to 1 due to the Q

output set at 0. Similarly the output of gate 4 is also set at 1 due to the K input set at 0. The

outputs of gates 1 and 2 remain unchanged as the inputs to gates 1 and 2 are both logic 1.

Assume the outputs of gates 1 and 2 to be 1 and 0 respectively. During the positive half cycle,

the clock input to gates 7 and 8 is inverted therefore both the gates are disabled and their

output is set to logic 1. With logic 1 at the inputs of gates 5 and 6 the output Q and Q remains

unchanged throughout the positive half of the clock cycle. During the negative half of the clock

cycle the Master flip-flop is disabled and the output of the Master flip-flop remains fixed during

the negative half cycle. The Slave flip-flop is enabled and the 1 and 0 outputs of the Master

flip-flop set the Q and Q output to 1 and 0 respectively.

Initially, if the Q and Q outputs are 0 and 1 respectively, setting the J and K inputs to 1

and 0 respectively sets the output to 1 and 0 respectively. During the positive half of the clock

the Master flip-flop is enabled, the output of gate 3 is set to 0 as the J, Q and CLK inputs are

all at logic 1. The output of gate 4 is set to 1 as the K input is logic 0. These inputs set the

output of the Master flip-flop at gates 1 and 2 to logic 1 and 0 respectively. During the negative

half of the clock cycle the Slave flip-flop is enabled the output Q and Q are set to logic 1 and 0

respectively.

257

CS302 - Digital Logic & Design

CLK

MASTER

SLAVE

Figure 25.2a Master-Slave flip-flop

The truth-table of the master-slave flip-flop is shown in table 25.2. The timing diagram

of the master-slave flip-flop is shown in figure 25.2b.

Input

Output

CLK

Qt+1

Pulse

Table 25.2

Truth table of the Master-Slave J-K flip-flop

CLK

Figure 25.2b Timing diagram of a Master Slave J-K flip-flop

Flip-Flop Operating Characteristics

The performance of the flip-flop is specified by several operating characteristics

mentioned in the data sheets of the flip-flops. The important operating characteristics are

258

CS302 - Digital Logic & Design

Propagation Delay

Set-up Time

Hold Time

Maximum Clock frequency

Pulse width

Power Dissipation

Propagation Delay

The propagation delay time is the interval of time when the input is applied and the

output changes. Four different types of Propagation Delays are measured.

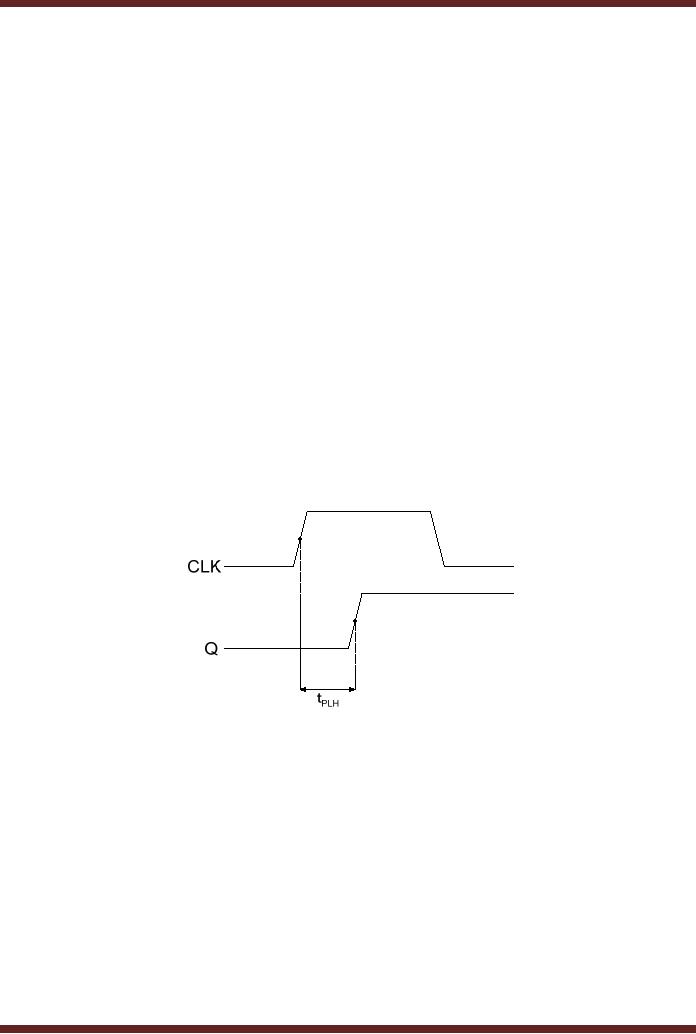
5. Propagtaion Delay tPLH measured with respect to the triggering edge of the clock to the

low-to-high transition of the output. Figure 25.3. On a positive or negative clock transition

the flip-flop changes its output state. The Propagation Delay is measured at 50% transition

mark on the triggering edge of the clock and the 50% mark on the low-to-high transition of

the output that occurs due to the clock transition.

6. Propagtaion Delay tPHL measured with respect to the triggering edge of the clock to the

high-to-low transition of the output. Figure 25.4. On a positive or negative clock transition

the flip-flop changes its output state. The Propagation Delay is measured at 50% transition

mark on the triggering edge of the clock and the 50% mark on the high-to-low transition of

the output that occurs due to the clock transition.

Figure 25.3

Propagation Delay, clock to low-to-high transition of the output

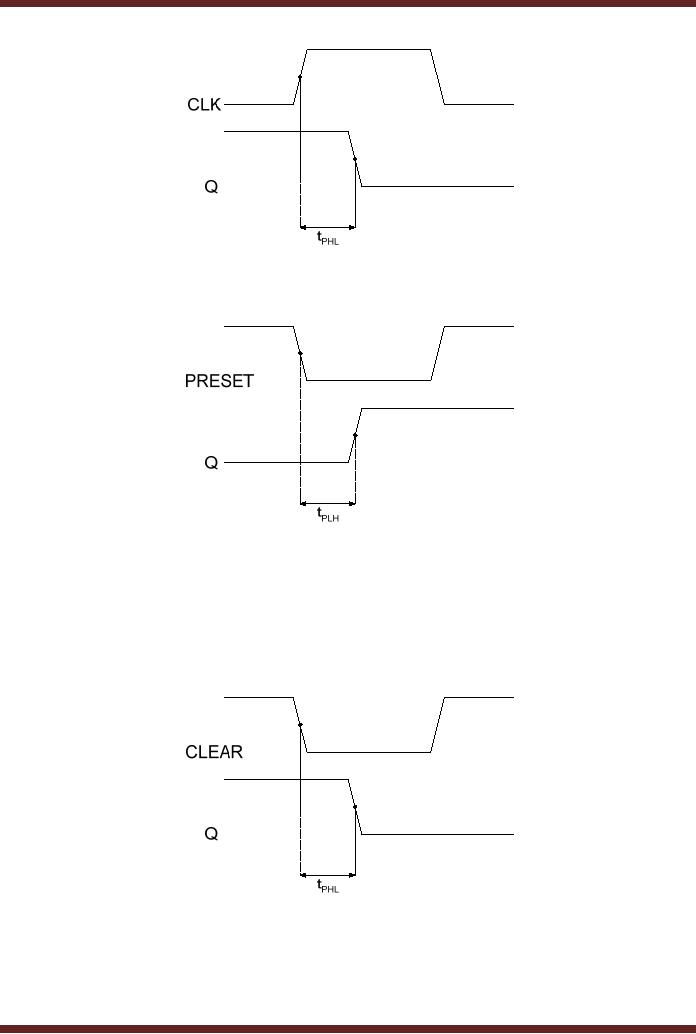
7. Propagtaion Delay tPLH measured with respect to the leading edge of the preset input to the

low-to-high transition of the output. Figure 25.5. On a high-to-low transition of the preset

signal the flip-flop changes its output state to logic high. The Propagation Delay is

measured at 50% transition mark on the triggering edge of the preset signal and the 50%

mark on the low-to-high transition of the output that occurs due to the preset signal.

259

CS302 - Digital Logic & Design

Figure 25.4

Propagation Delay, clock to high-to-low transition of the output

Figure 25.5

Propagation Delay, preset to low-to-high transition of the output

8. Propagtaion Delay tPHL measured with respect to the leading edge of the clear input to the

high-to-low transition of the output. Figure 25.6. On a high-to-low transition of the clear

signal the flip-flop changes its output state to logic low. The Propagation Delay is

measured at 50% transition mark on the triggering edge of the clear signal and the 50%

mark on the high-to-low transition of the output that occurs due to the preset signal.

Figure 25.6

Propagation Delay, clear to high-to-low transition of the output

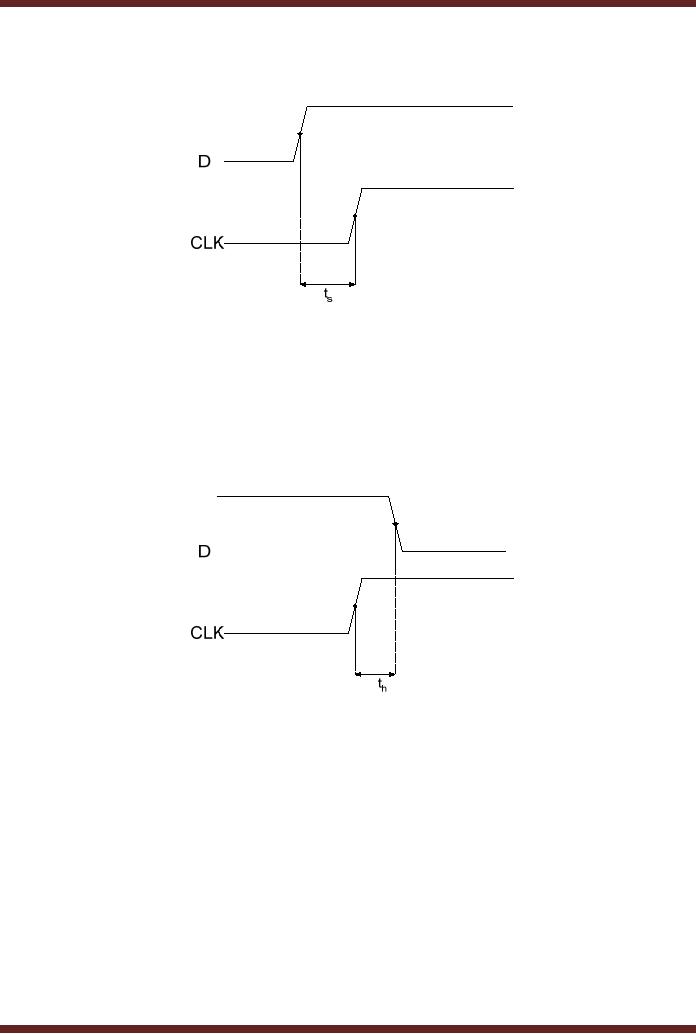
Set-up Time

When a clock transition occurs at the clock input of a flip-flop the output of the flip-flop

is set to a new state based on the inputs. For the flip-flop to change its output to a new state at

the clock transition, the input should be stable. The minimum time required for the input logic

260

CS302 - Digital Logic & Design

levels to remain stable before the clock transition occurs is known as the Set-up time. Figure

25.7

Figure 25.7

Set-up time for a D flip-flop

Hold Time

The input signal maintained at the flip-flop input has to be maintained for a minimum

time after the clock transition for the flip-flop to reliably clock in the input signal. The minimum

time for which the input signal has to be maintained at the input is the Hold time of the flip-flop.

Figure 25.8

Hold time for a D flip-flop

Maximum Clock Frequency

A flip-flop can be operated at a certain clock frequency. If the clock frequency is

increased beyond a certain limit the flip-flop will be unable to respond to the fast changing

clock transitions, therefore the flip-flop will be unable to function. The maximum clock

frequency fmax is the highest rate at which the flip-flop operates reliably.

Pulse Width

A flip-flop uses the clock, preset and clear inputs for its operation. Each signal has to

be of a specified duration for correct operation of the flip-flop. The manufacturer specifies the

minimum pulse width tw for each of the three signals. The clock signal is specified by minimum

high time and minimum low time.

261

CS302 - Digital Logic & Design

Power Dissipation

A flip-flop consumes power during its operation. The power consumed by a flip-flop is

defined by P = Vcc x Icc. The flip-flop is connected to +5 volts and it draws 5 mA of current

during its operation, therefore the power dissipation of the flip-flop is 25 mW.

A digital circuit is made of a number of gates, functional units and flip-flops. The total

power requirement of each device should be known so that an appropriate dc power source is

used to supply power to the digital circuit.

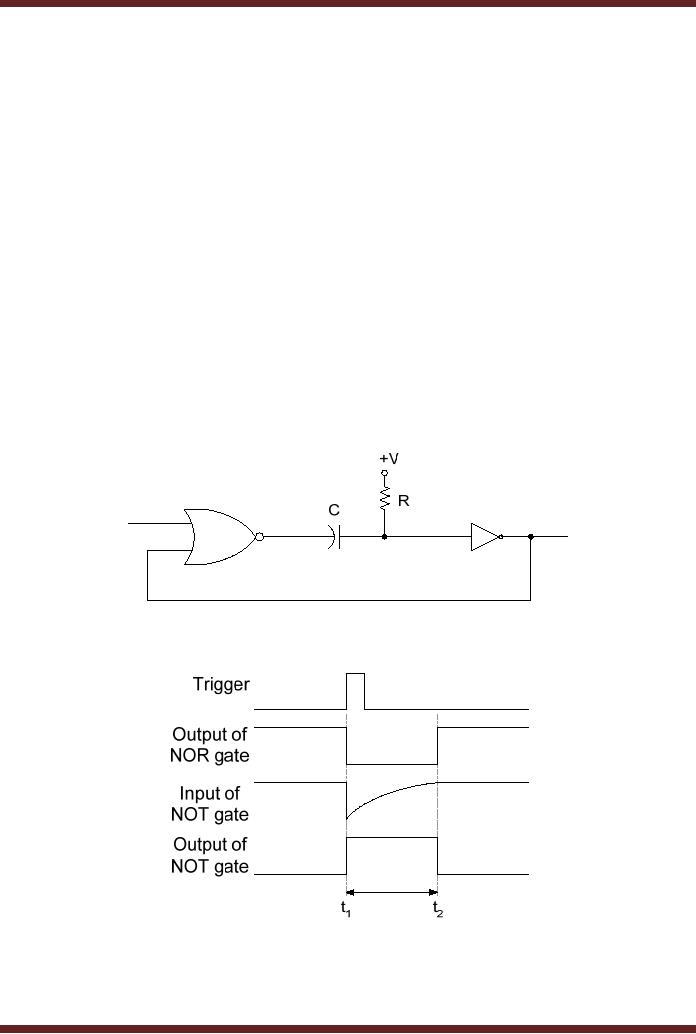
One-Shot Mono-stable multi-vibrator

Bi-stable devices remain in either of their two states unless the inputs force the device

to switch its state. The device remains in its alternate state unless the inputs are changed

again to force the device back to its original state. A mono-stable device only has a single

stable state and it remains in its stable state. It temporarily changes to its unstable state when

it is triggered. It remains in its unstable state for a predetermined length of time and then it

automatically switches back to its stable state. The length of time for which the device remains

in the unstable state is determined by the time constant determined by the Resistor and

Capacitor connected externally to the mon-stable device. The output of the device is a pulse

having a time duration determined by R and C. These mono-stable devices are also known as

One-Shots. Figure 25.9. One-Shots are of two types, the nonretriggerable and retriggerable.

Figure 25.9a Circuit diagram of a One-Shot

Figure 25.9b Timing diagram of a One-Shot

The One-Shot is triggered by applying a short pulse at the input of the NOR gate at

time interval t1. The One-Shot is in its stable state with output at logic zero at time interval < t1.

The logic high triggering pulse at the input of the NOR gate sets its output to logic low. The

262

CS302 - Digital Logic & Design

logic low output of the NOR gate is inverted into logic high by the NOT gate and the One-Shot

is in unstable state at the start of interval t1. The logic high output of the NOT gate is

connected back to the second input of the NOR gate, which maintains the output of the NOR

gate at logic low. When the output of the NOR gate is set to logic low at interval t1, the

capacitor C begins charging through the Resistor R. The charging time (in seconds) is

determined by the time constant RC. During the charging of the capacitor during interval t1 to

t2, the input of the NOT gate remains at logic low, therefore the output of the NOT gate

remains in the unstable state at logic high. When the capacitor is fully charged to potential +V

(logic high) at time interval t2, the NOT gate input also become logic high, which sets the

output of the NOT gate to logic low. With the setting of the NOT gate output to logic low at

interval t2, the One-Shot id switched back to its stable state. The interval t1 to t2 during which

the One-Shot is in its unstable state is determined by the time constant RC.

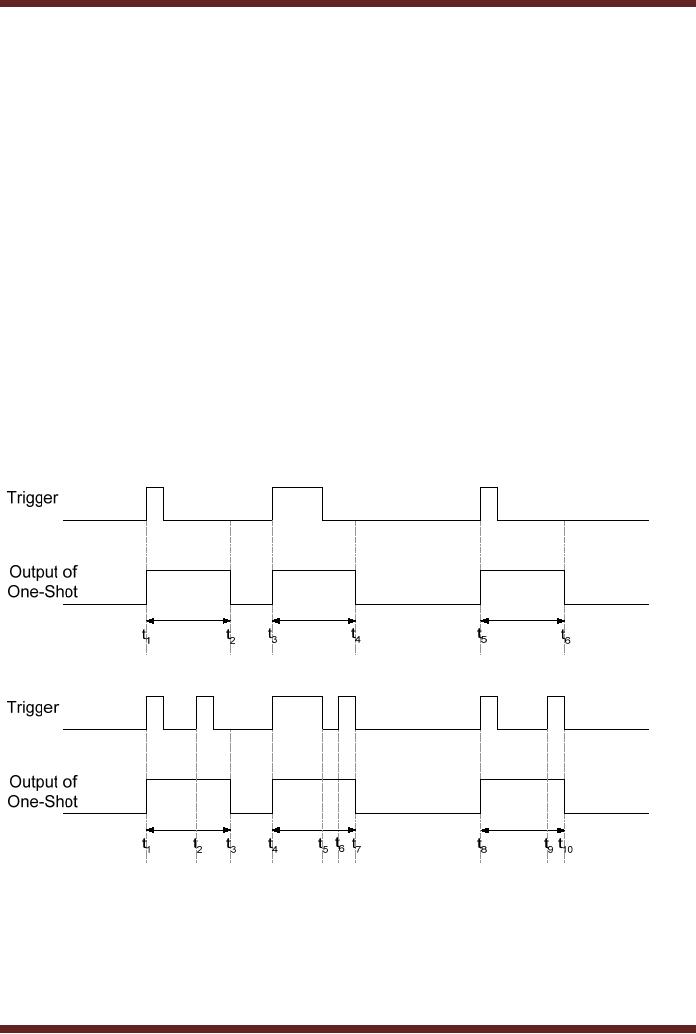
1. Nonretriggerable One-Shot

A nonretriggerable OneShot is triggered to its unstable state.

a. The One-Shot output remains in the unstable state for a fixed period of time on each

trigger input.

b. The One-Shot will have to return to its stable state before it can be triggered again. If it is

already in its unstable state due to application of a trigger input, a new trigger input will

have no effect.

c. The duration of trigger input pulses has no effect on the output pulse duration. The One-

Shot is triggered either on the positive or the negative edge. Figure 25.10

Figure 25.10a Timing diagram of a non-retriggerable One-Shot

Figure 25.10b Timing diagram of a non-retriggerable One-Shot with ignored triggers

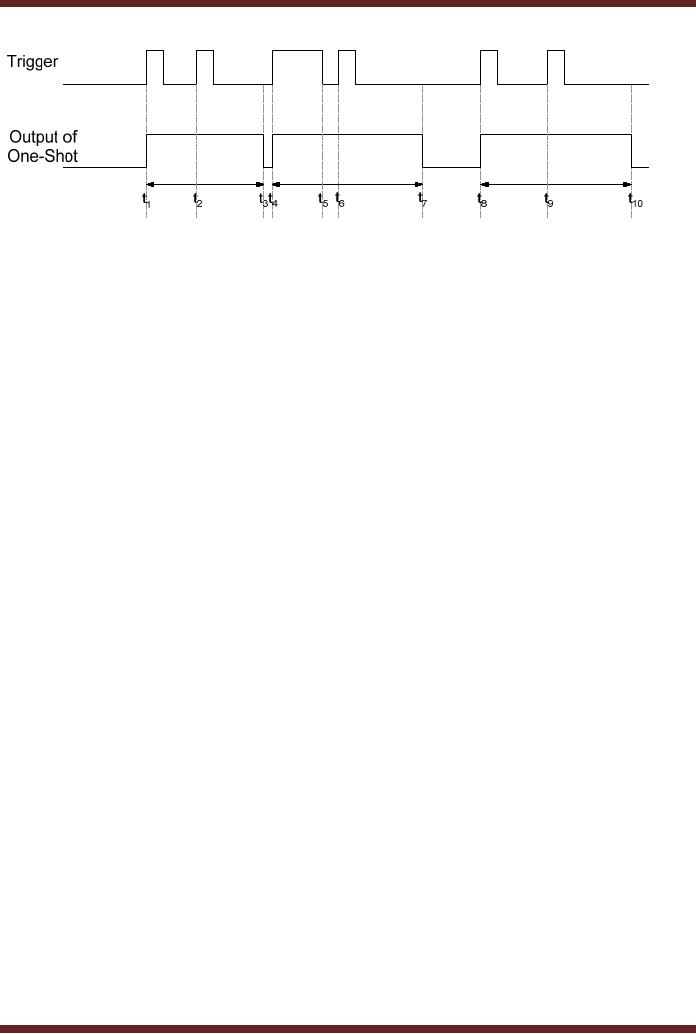
2. Retriggerable One-Shot

A retriggerabe One-Shot operation is very similar to that of the Nonretriggerbale One-Shot

except that the retriggerable One-Shot will retrigger even if it is in its unstable state. Figure

25.11. The retriggerable and Nonretriggerbale are available in Integrated Circuit form.

263

CS302 - Digital Logic & Design

Figure 25.11 Timing diagram of a Retriggerable One-Shot

264

Table of Contents: