Implementation of Quad MUX, Latches and Flip-Flops

<< OLMC for GAL16V8, Tri-state Buffer and OLMC output pin

APPLICATION OF S-R LATCH, Edge-Triggered D Flip-Flop, J-K Flip-flop >>

CS302 - Digital Logic & Design

Lesson No. 22

ABEL INPUT FILE OF A QUAD 1-OF-4 MUX

A Quad 1-of-4 MUX has four Multiplexers, each Multiplexer has four inputs and a

single output. Each multiplexer has two select inputs to select one of the four inputs. The two

select inputs are common to all the four multiplexers. The function table of the Quad 1-of-4

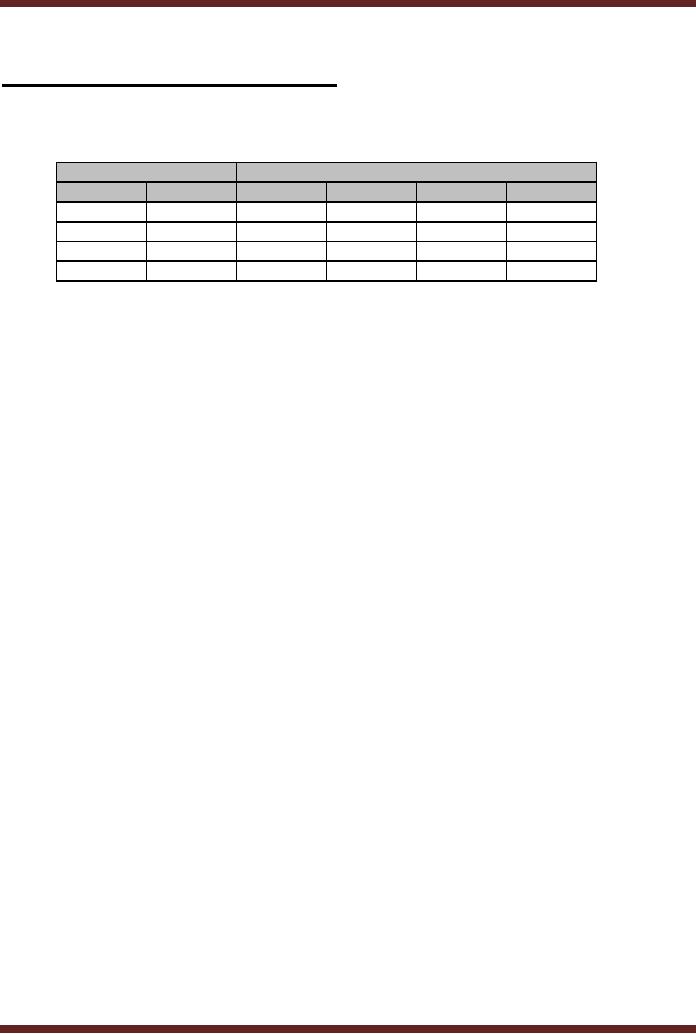
MUX is shown in table 22.1.

Select Inputs

Outputs

Dout

Cout

Bout

Aout

Table 22.1

Truth table of a Quad 1-of-4 Multiplexer

Module quad_1of4_mux

Title

`Quad 1 of 4 multiplexer in a GAL20V8'

mux

device

`P20V8';

A0, A1, A2, A3

pin 1, 2, 3, 4;

B0, B1, B2, B3

pin 5, 6, 7, 8;

C0, C1, C2, C3

pin 9, 10, 11, 13;

D0, D1, D2, D3

pin 14, 15, 16, 17;

Aout, Bout, Cout, Dout

pin 21, 20, 19, 18;

S0, S1

pin 22, 23;

Equations

Aout = !S1 & !S0 & A0 # !S1 & S0 & A1 # S1& !S0 & A2 # S1 & S0 & A3;

Bout = !S1 & !S0 & B0 # !S1 & S0 & B1 # S1& !S0 & B2 # S1 & S0 & B3;

Cout = !S1 & !S0 & C0 # !S1 & S0 & C1 # S1& !S0 & C2 # S1 & S0 & C3;

Dout = !S1 & !S0 & D0 # !S1 & S0 & D1 # S1& !S0 & D2 # S1 & S0 & D3;

Test_vectors

([S1, S0, A0, A1, A2, A3, B0, B1, B2, B3, C0, C1, C2, C3, D0, D1, D2, D3] →

[Aout, Bout, Cout, Dout])

"S S A A A A B B B B C C C C D D D D outputs

"0 1 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3

A B C D

[0, 0,

0, 0,

1, 0,

0, 0,

→

[1,

0];

[0, 1,

0, 0,

1, 0,

0, 0,

→

[0,

0];

[1, 0,

0, 0,

1, 0,

0, 0,

→

[0,

0];

[1, 1,

0, 0,

1, 0,

0, 0,

→

[0,

1];

[0, 0,

0, 1,

1, 1,

→

[1,

0];

[0, 1,

0, 1,

1, 1,

→

[1,

1];

[1, 0,

0, 1,

1, 1,

→

[1,

1];

[1, 1,

0, 1,

1, 1,

→

[0,

1];

END

Figure 22.1

ABEL Input file for the Quad 1-of-4 MUX

216

CS302 - Digital Logic & Design

Implementation of Quad MUX

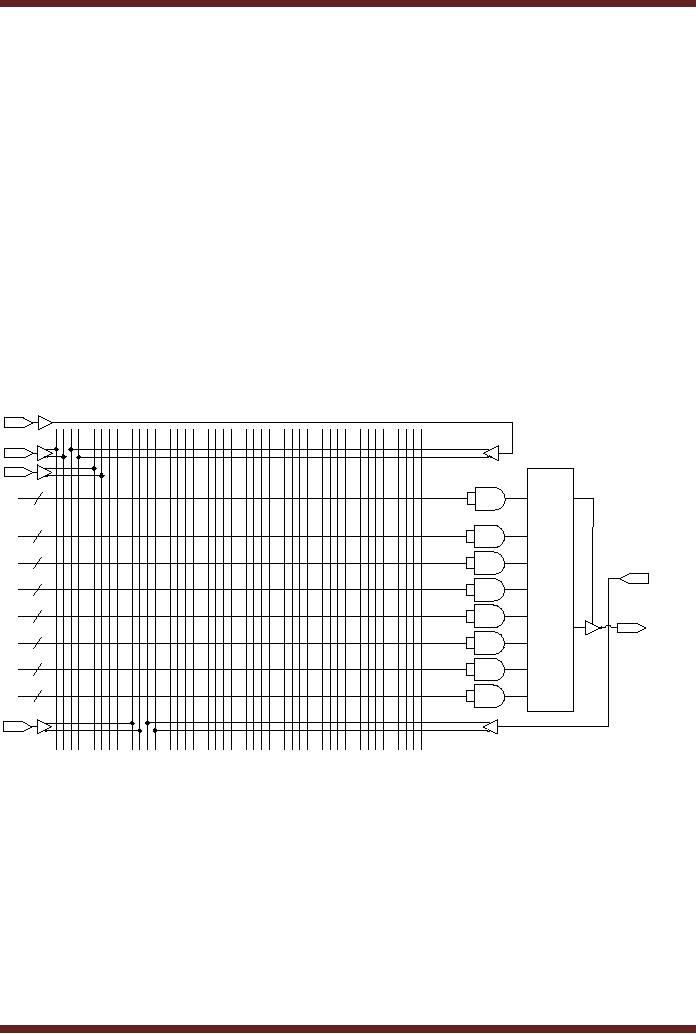
The Quad Multiplexer has 16 inputs, 4 inputs for each Multiplexer. Each multiplexer

has a single output, therefore a total of 4 outputs are required. To select an appropriate

multiplexer input there are two select input lines connected to all the four multiplexers. The

Quad Multiplexer has a total of 22 pins through which the device is operated. The GAL16V8

device can not be used as it does not enough pins to implement the quad multiplexer. The

GAL20V8 PLD is used for the implementation of the Quad 1-of-4 Multiplexer. The device has

12 inputs, 2 special function inputs and 8 input/output pins. Four input/output pins of the GAL

device are configured as inputs to support the fourth multiplexer inputs D1, D2 and D3 and the

select input S0.

Each Multiplexer output Aout , Bout, Cout and Dout is represented by a Sum-of-

product Boolean expression, each having four product terms. Refer to figure 21.16. Thus each

of the four OLMCs which are connected to the four output pins have four product terms

connected to the inputs of the OR gates. The implementation of the multiplexer function Aout

is shown in figure 22.2.

Input Lines

x x

OLMC

Aout

Figure 22.2

Implementation of 1-of-4 Multiplexer

Sequential Circuits

The combinational digital circuits have no storage element; therefore combinational

circuits handle only instantaneous inputs. The outputs of the combinational circuits also can

not be stored. The absence of a memory element restricts the use of digital combinational

circuits to certain application areas. The use of a memory element which is capable of storing

digital inputs and outputs is an important part of all practical digital circuits.

Consider an ALU which performs Arithmetic and Logical operations. An ALU can not

perform its operations unless it is connected to memory elements that store the inputs applied

at the inputs of the ALU and outputs from the ALU. Consider an ALU that performs addition

operation on a set of numbers, 2, 3, 4 and 5. The ALU can add two numbers at a time;

217

CS302 - Digital Logic & Design

therefore the ALU has to add the four numbers two at a time. The four numbers have to be

stored temporarily, the partial results after adding two numbers also need to be stored. To add

the four numbers, the first two numbers 2 and 3 stored in two separate memory elements are

added together, the result (5) has to be added to the next number 4. The result (5) is

temporarily stored in one of the two memory elements used to store the numbers 2 and 3. The

result (5) is added to the third number 4 to provide another partial sum result 9 which has to be

stored and then added with the fourth number 5.

In a parallel-to-serial conversion of byte data using a multiplexer and the conversion

from serial-to-parallel using a demultiplexer, memory elements are required that store the byte

data at the input of the multiplexer for conversion into serial information and another memory

element at the output of the demultiplexer for conversion back to parallel.

The counter circuit used in digital circuits count to the next value because of the

memory element which stores and remembers the previous count value. A counter can not

operate without a memory element.

Digital circuits that use memory elements for their operation are known as Sequential

circuits. Thus Sequential circuits are implemented by combining combinational circuits with

memory elements.

Latches and Flip-Flops

A latch is a temporary storage device that has two stable states. A latch output can

change from one state to the other by applying appropriate inputs. A latch normally has two

inputs, the binary input combinations at the latch input allows the latch to change its state. A

latch has two outputs Q and its complement Q . The latch is said to be in logic high state when

Q=1 and Q =0 and it is in the logic low state when Q=0 and Q =1. When the latch is set to a

certain state it retains its state unless the inputs are changed to set the latch to a new state.

Thus a latch is a memory element which is able to retain the information stored in it.

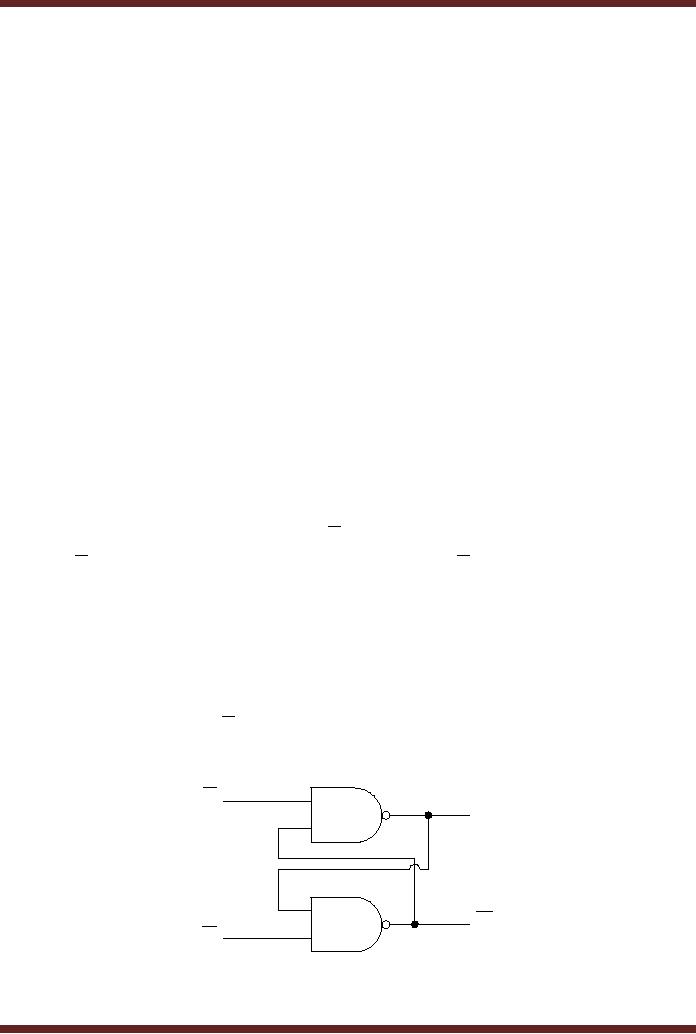
The NAND gate based S-R (Set-Reset) Latch

An S-R Latch is implemented by connecting two NAND gates together. The output of

each NAND gate is connected to the input of the other NAND gate. The unconnected inputs of

the two NAND gates are the Set S and Reset R inputs. The outputs of the two NAND gates

are the Q and its complement Q . The circuit diagram of the NAND based S-R latch is shown in

figure 22.3

Figure 22.3

NAND based S-R Latch

218

CS302 - Digital Logic & Design

The S-R latch has two inputs, therefore four different combinations of inputs can be

applied to control the operation of the S-R latch. The four possible input combinations are

1. Inputs S=0 & R=0

a. Assume that the outputs Q and Q are set at logic 1 and logic 0 respectively. Since both

the inputs S and R are logic low, therefore both the Q and Q outputs are set to 1. The

inputs S = 0 and R = 0 are never applied as these inputs result in invalid output states as Q

and Q should be complements of each other.

b. Assume that the outputs Q and Q are set at logic 0 and logic 1 respectively. Since both

the inputs S and R are logic low, therefore both the Q and Q outputs are set to 1. The

inputs S = 0 and R = 0 are never applied as these inputs result in invalid output states as Q

and Q should be complements of each other.

The input combination S=0 and R=0 is considered to be invalid as it results in an

invalid output of Q=1 and Q =1.

2. Inputs S=0 & R=1

a. Consider that the outputs Q and Q have 1 and 0 logic states. The Set input S = 0 sets the

output Q to 1. The Q input and the R inputs to gate 2 are both at logic 1, therefore the

output Q is set to 0.

b. Consider that initially the Q and Q outputs are at logic state 0 and 1 respectively. The Set

input S = 0 sets the output Q to 1. The Q input and the R inputs to gate 2 are both at logic

1, therefore the output Q is set to 0.

Thus what ever the initial outputs, setting S to 0 and R to 1 sets the Q and Q outputs

to 1 and 0 respectively.

3. Inputs S=1 & R=0

a. Initially, the Q and Q outputs are at 1 and 0 respectively. The Reset input R=0 sets the

output Q to 1. The inputs of gate 1, Q and S are both at logic 1, therefore the output Q is

set to 0.

b. Initially, if the Q and Q outputs are at logic 0 and 1 respectively, setting R to 0 sets Q to 1.

The inputs of gate 1, Q and S are both at logic 1, therefore the output Q is set to 0.

Thus, what ever the outputs, setting S to 1 and R to 0 sets the Q and Q outputs to 0

and 1 respectively.

4. Inputs S=1 & R=1

219

CS302 - Digital Logic & Design

a. Initially, the Q and Q outputs are at 1 and 0 respectively. The inputs of gate 2 , Q and R

are both at logic 1, therefore the output Q is set to 0. The inputs of gate 1, Q and S are 0

and 1 respectively, therefore the output is set to 1.

b. Initially, the Q and Q outputs are at 0 and 1 respectively. The inputs of gate 2 , Q and R

are at logic 0 and 1 respectively, therefore the output Q is set to 1. The inputs of gate 1,

Q and S are both at logic 1 respectively, therefore the output is set to 0.

Thus, with S and R inputs both set to logic 1, the previous output state is maintained. If

initially, the Q and Q are at logic 1 and 0 respectively, setting S=1 and R=1 maintains the same

outputs. Similarly, if initially Q and Q are at logic 0 and 1 respectively, setting S=1 and R=1

maintains the same outputs.

A truth-table shows the operation of the S-R NAND based latch. Table 22.2. The

Output Qt+1 represents the Q output of NAND gate 1 at time interval t+1.When inputs are S = 1

and R = 1 the next state output Qt+1 remains the same as the previous state output Qt. When

inputs are S = 0 and R = 1 the output Q is set to 1. When inputs are S = 1 and R = 0 the output

Q is set to 0. Inputs S = 0 and R = 0 are not applied as they place the latch in an invalid state.

The NAND gate based S-R latch has active-low inputs.

Input

Output

Qt+1

invalid

Table 22.2

Truth-Table of NAND based S-R Latch

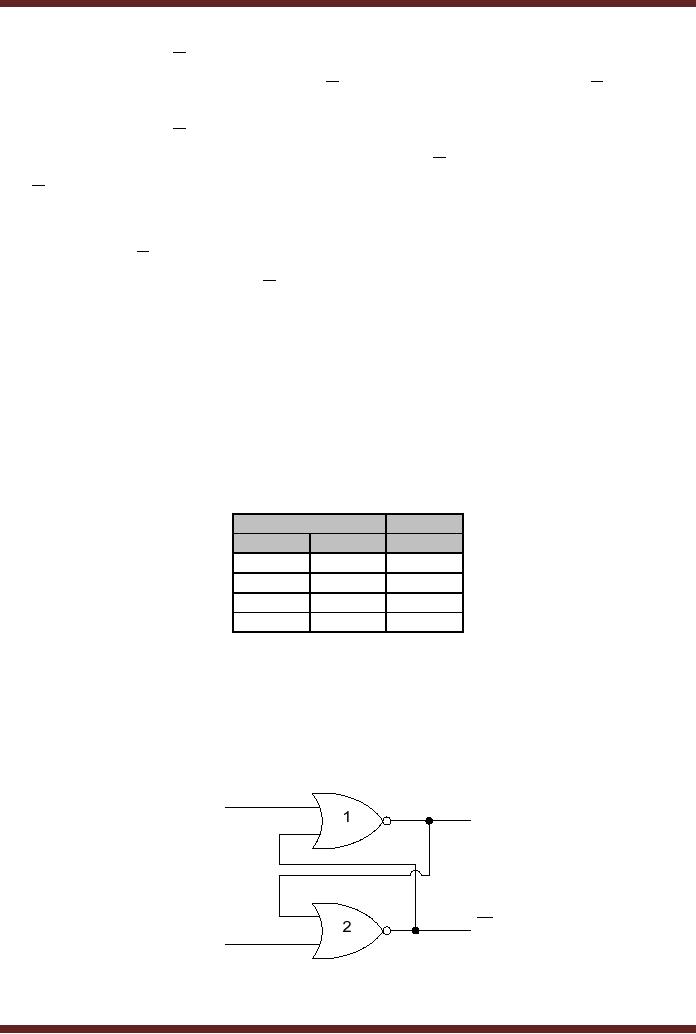
The NOR gate based S-R (Set-Reset) Latch

A NOR based S-R latch is implemented using NOR gates instead of NAND gates.

Connections are identical to that of the NAND based latch. The S and R inputs have been

switched. Figure 22.2.

Figure 22.4

NOR based S-R Latch

220

CS302 - Digital Logic & Design

The S-R NOR based latch has two inputs, therefore four different combinations of

inputs can be applied to control the operation of the S-R latch. The four possible input

combinations are

1. Inputs S=0 & R=0

a. Assume that the outputs Q and Q are set at logic 1 and logic 0 respectively. The R and Q

inputs at gate 1 are both at logic 0, therefore the Q output is set to logic 1. The S and Q

inputs at gate 2 are at logic 0 and 1 respectively, therefore the output Q is set to logic 0.

b. Assume that the outputs Q and Q are set at logic 0 and logic 1 respectively. The S and Q

inputs at gate 2 are both at logic 0, therefore the Q output is set to logic 1. The R and Q

inputs at gate 1 are at logic 0 and 1 respectively, therefore the output Q is set to logic 0.

Thus, with S and R inputs both set to logic 0, the previous output state is maintained. If

initially, the Q and Q are at logic 1 and 0 respectively, setting S=0 and R=0 maintains the same

outputs. Similarly, if initially Q and Q are at logic 0 and 1 respectively, setting S=0 and R=0

maintains the same outputs.

2. Inputs S=0 & R=1

a. Consider that the outputs Q and Q have 1 and 0 logic states. The Reset input R = 1 sets

the output Q to 0. The Q input and the S inputs to gate 2 are both at logic 0, therefore the

output Q is set to 1.

b. Consider that initially the Q and Q outputs are at logic state 0 and 1 respectively. The

Reset input R = 1 sets the output Q to 0. The Q input and the S inputs to gate 2 are both at

logic 0, therefore the output Q is set to 1.

Thus what ever the initial outputs, setting S to 0 and R to 1 sets the Q and Q outputs

to 0 and 1 respectively.

3. Inputs S=1 & R=0

a. Initially, the Q and Q outputs are at 1 and 0 respectively. The Set input S=1 sets the

output Q to 0. The inputs of gate 1, Q and R are both at logic 0, therefore the output Q is

set to 1.

b. Initially, if the Q and Q outputs are at logic 0 and 1 respectively, setting S to 1 sets Q to 0.

The inputs of gate 1, Q and R are both at logic 0, therefore the output Q is set to 1.

Thus, what ever the outputs, setting S to 1 and R to 0 sets the Q and Q outputs to 1

and 0 respectively.

4. Inputs S=1 & R=1

a. Initially, the Q and Q outputs are at 1 and 0 respectively. Since both the inputs S and R

are logic 1, therefore both the Q and Q outputs are set to 0. The inputs S = 1 and R = 1

221

CS302 - Digital Logic & Design

are never applied as these inputs result in invalid output states as Q and Q should be

complements of each other.

b. Initially, the Q and Q outputs are at 0 and 1 respectively. Since both the inputs S and R

are logic 1, therefore both the Q and Q outputs are set to 0. The inputs S = 1 and R = 1

are never applied as these inputs result in invalid output states as Q and Q should be

complements of each other.

The input combination S=1 and R=1 is considered to be invalid as it results in an

invalid output of Q=0 and Q =0.

The truth table of the NOR gate based latch is shown. Table 22.3. When inputs are S =

0 and R = 0 the next state output Qt+1 remains the same as the previous state output Qt. When

inputs are S = 0 and R = 1 the output Q is set to 0. When inputs are S = 1 and R = 0 the output

Q is set to 1. Inputs S = 1 and R = 1 are not applied as they place the latch in an invalid state.

The NOR gate based S-R latch has active-high inputs.

Input

Output

Qt+1

invalid

Table 22.3

Truth-Table of NOR based S-R Latch

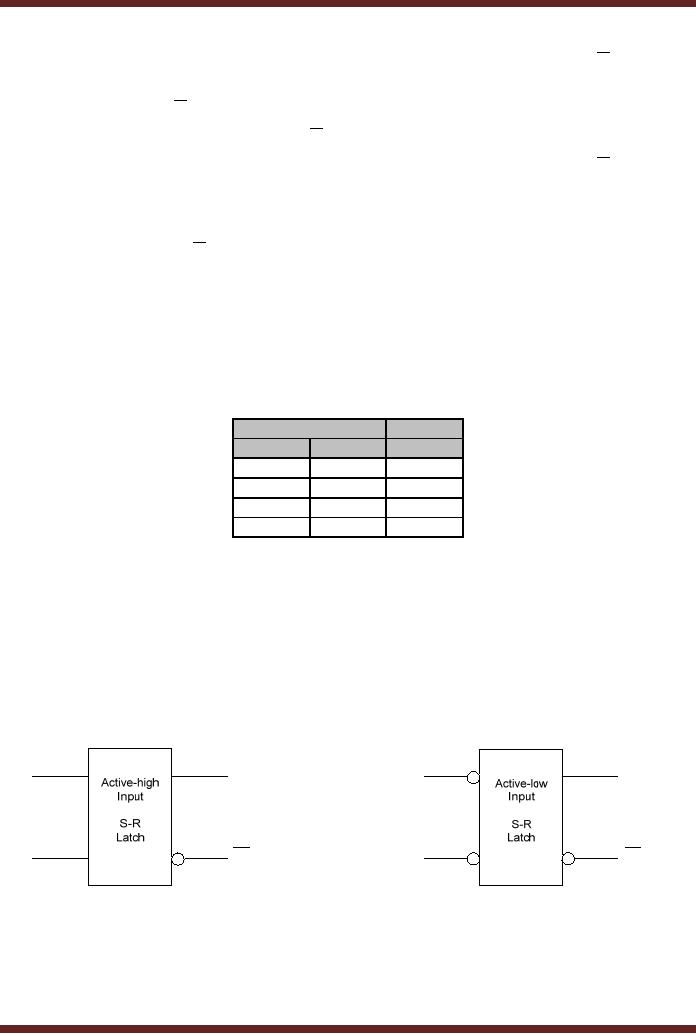
Comparing the operation of the NOR based and NAND based S-R latches. The NAND

based latch has active-low inputs, where as NOR based latch has active-high inputs. Both the

S-R latches are set to logic 1 when the set input is activated and the reset input is inactive.

Both the latches are set to logic 0 when the reset input is activated and the set input is

inactive. The latches maintain the output state when both the set and reset inputs are inactive.

For both the latches both the set and reset inputs can not be activated simultaneously as this

leads to invalid output states. The Logic symbols of the two latches are shown in figure 22.5.

Figure 22.5

NOR based Active-High and NAND based Active-Low S-R Latches

S-R Latch Timing Diagrams

The operation of the active-high and active-low input latches can be understood with

the help of timing diagrams. Figure 22.6 shows the timing diagrams of the active high and

active-low input latches respectively. In the timing diagram of the NAND based S-R flip-flop,

222

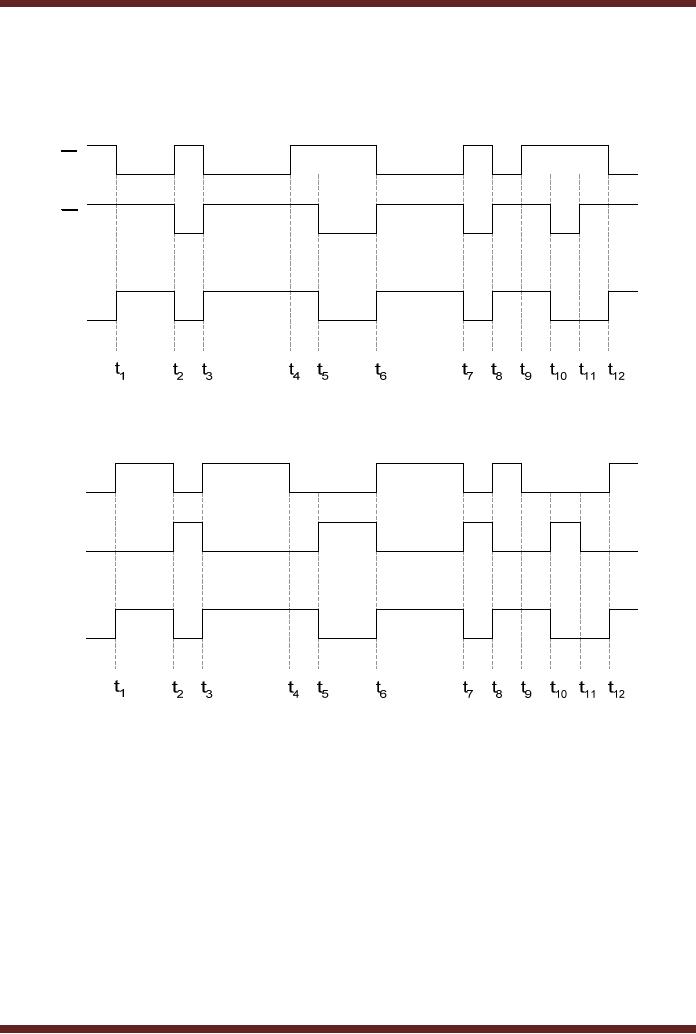
CS302 - Digital Logic & Design

the inputs S=0 and R=0 are not applied as it results in an invalid output state. Similarly, in the

timing diagram of the NOR based S-R flip-flop, the inputs S=1 and R=1 are not applied as it

results in an invalid output state.

Figure 22.6a Timing diagram of an active-low input S-R latch

Figure 22.6b Timing diagram of an active-high input S-R latch

223

Table of Contents: