OLMC Combinational Mode, Tri-State Buffers, The GAL16V8, Introduction to ABEL

<< Applications of Demultiplexer, PROM, PLA, PAL, GAL

OLMC for GAL16V8, Tri-state Buffer and OLMC output pin >>

CS302 - Digital Logic & Design

Lesson No. 20

IMPLEMENTING CONSTANT 0S AND 1S

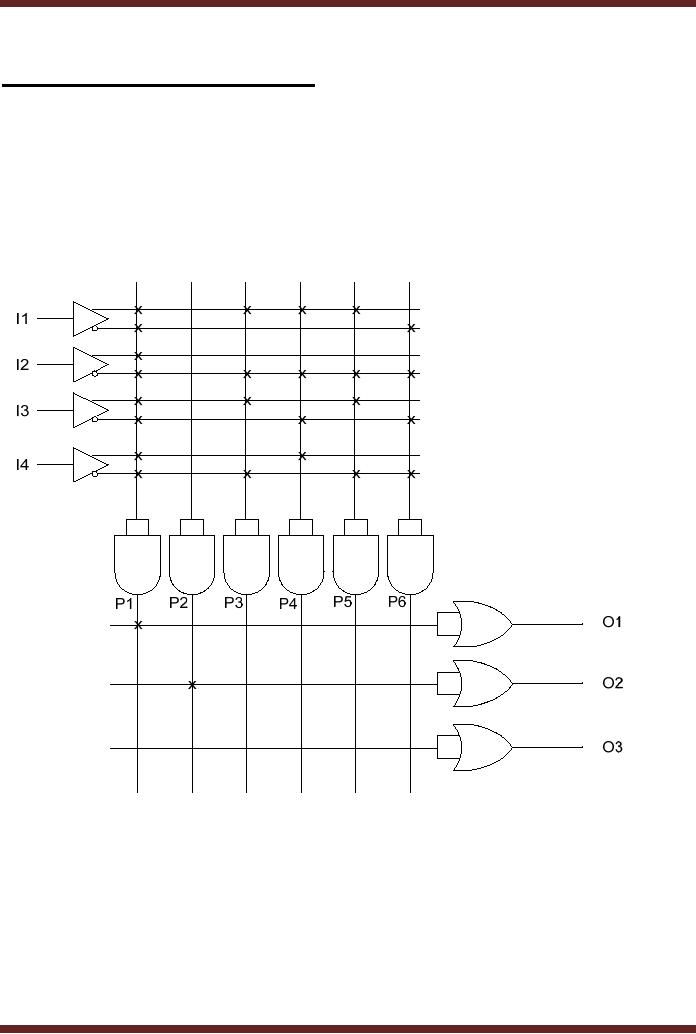
The PLA can be programmed to give an output of constant 0 or 1. Figure 20.1. All the

four inputs and their complements are shown connected to the first AND gate. The product

term generated by the AND gate is 0. P1 = 0 . The P1 product term is connected to the input of

first OR gate. Thus the output of OR gate is 0. The inputs to the second AND gate are

disconnected, thus the product term generated by the AND gate is a 1. P2 = 1 . The P2 term is

connected to the input of the second OR gate, therefore the output of the second OR gate is a

1. No product term is connected to the input of the third OR gate, therefore the output of the

third OR gate is 0.

Figure 20.1

4 x 3 PLA Device programmed for 0, 1 and 0 output

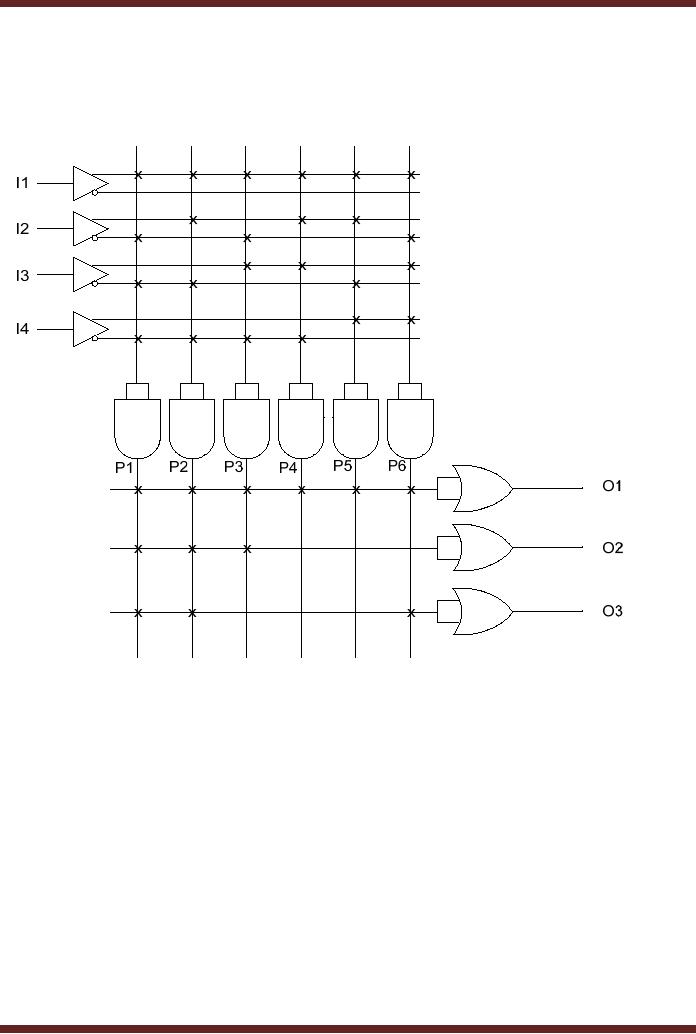
Implementing Odd-Prime Number Function

The Odd-Prime Number generator can be implemented by programming the 4 x 3 PLA.

Due to the limitations of the PLA which only has six product term (six AND gates), only the first

six Odd-Prime numbers 1, 3, 5, 7, 11 and 13 can be detected. Additional two outputs are

programmed to detect Odd-Prime multiples of 15 and 39 respectively. The six product terms

represented by P1, P2, P3, P4, P5 and P6 are minterms 1, 3, 5, 7, 11 and 13. The first OR

gate sums the six minterms (product terms) to give an output of 1 when any one of the first six

Odd-Prime numbers is applied at the inputs I1, I2, I3 and I4 of the PLA respectively. The

second OR gate sums the minterms 1, 3 and 5. Thus the output of the second OR gate is a 1

190

CS302 - Digital Logic & Design

when any of the three minterms is applied at the PLA inputs. Similarly, the third OR gate sums

the minterms 1, 3 and 13 and the output is set to logic 1 when any one of the three inputs are

detected at the input of the PLA. Figure 20.2.

Figure 20.2

4 x 3 PLA Device programmed to Detect Odd-Prime Numbers

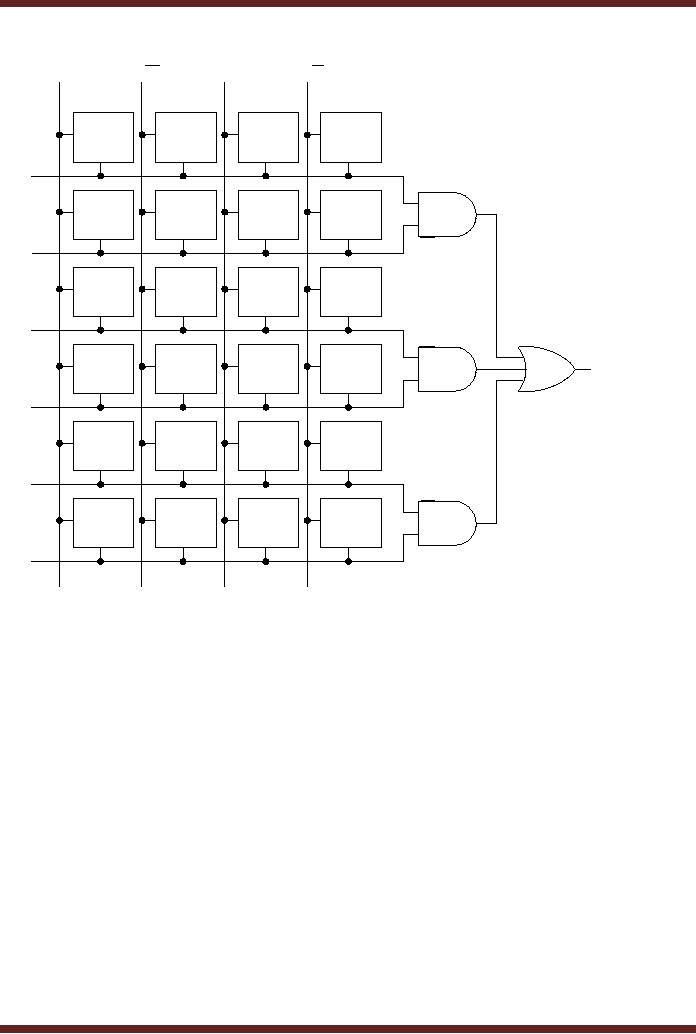
GAL Operation

The GAL has a reprogrammable AND gate array and a fixed OR array. GAL can be

reprogrammed as instead of fuses E2CMOS logic is used which can be programmed to

connect a column with a row. The E2CMOS logic at each columnrow intersection is known as

a cell. Figure 20.3. The E2CMOS cell in the `on' state connects the column with the row and a

cell in the `off' state disconnects the column and row. Appropriate cells are programmed to the

`on' state to allow appropriate literals to be connected to the AND gates which generate

product terms. The simplified GAL structure shows the implementation of an SOP function.

Figure 20.4

191

CS302 - Digital Logic & Design

E2CMOS

Simplified E2CMOS array structure of GAL

Figure 20.3

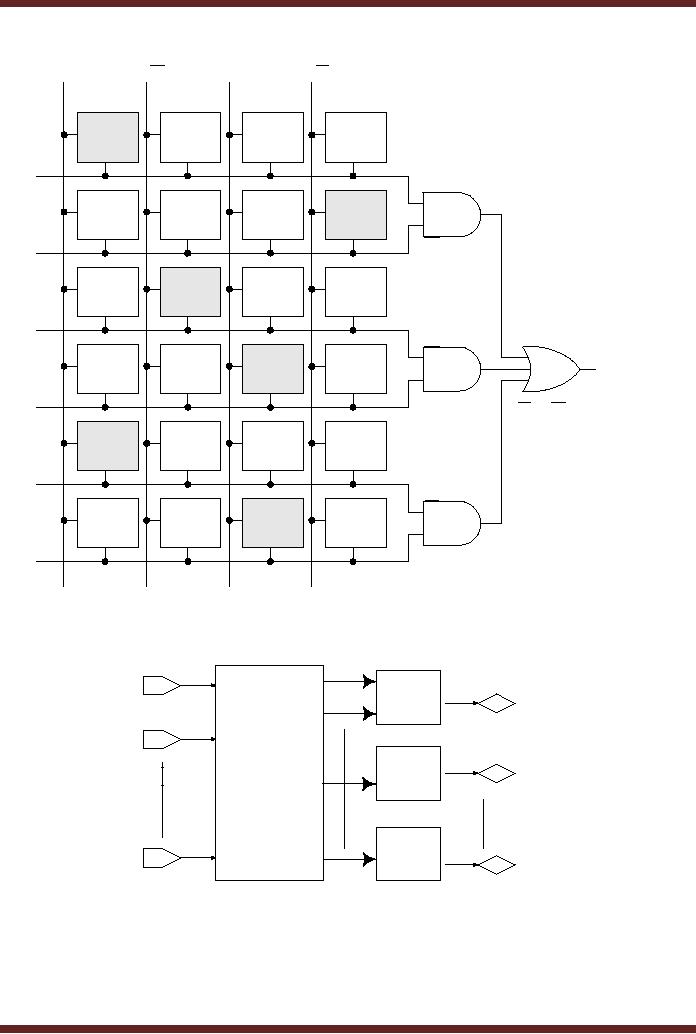
A typical Gal has eight or more inputs to the reprogrammable AND array and 8 or more

input/outputs from its `Output Logic Macro Cells' OLMCs. The OLMCs can be programmed to

Combinational Logic or Registered Logic. Combinational Logic is used for combinational

circuits, where as Registered Logic is based on Sequential circuits. Figure 20.5

192

CS302 - Digital Logic & Design

OFF

AB + AB + AB

OFF

Figure 20.4

GAL implementation of an SOP function

Input 1

Input/

OLMC

Output 1

Input 2

E2CMOS

Input/

Programmable

OLMC

AND array

Output 2

Input/

Input n

OLMC

Output m

Figure 20.5

Block diagram of a GAL

193

CS302 - Digital Logic & Design

GALs are also available in a variety of configurations. GALs are identified by a prefix

GAL followed by a 2-digt number indicating the number of inputs which is followed by V

indicating variable output configuration followed by a number which indicates the number of

outputs. Figure 20.6

G A L 16 V 8

Generic array Logic

Eight Outputs

Variable output Configuration

Sixteen Inputs

Figure 20.6

Standard GAL Numbering

Programming of PLDs

PLDs are programmed with the help of computer which runs the programming

software. The computer is connected to a programmer socket in which the PLD is inserted for

programming. PLDs can also be programmed when they are installed on a circuit board.

The programming of a PLD device involves entering the logic function in the form of a

Boolean equation, truth table or a state diagram. Any errors during the entry process are

corrected. The software compiler processes the information in the input file and translates it

into a suitable format. The complier also minimizes the logic. The minimized logic is then

tested by using a set of hypothetical inputs known as test vectors. The testing verifies the

design of the logic circuit before committing it to the PLD. If any flaws are detected during the

testing process the design must be debugged and submitted for recompilation. Once the

design has been finalized a documentation file is produced along with a fuse map file which is

downloaded to the programmer which programs the PLD device inserted in the programmer

socket.

PLDs have In-System Programming (ISP) capability that allows the PLDs to be

programmed after they have been installed on a circuit board. A standard 4-wire interface is

used for programming the In-System PLD. ISP capability allows systems to be upgraded by

reprogramming the PLD.

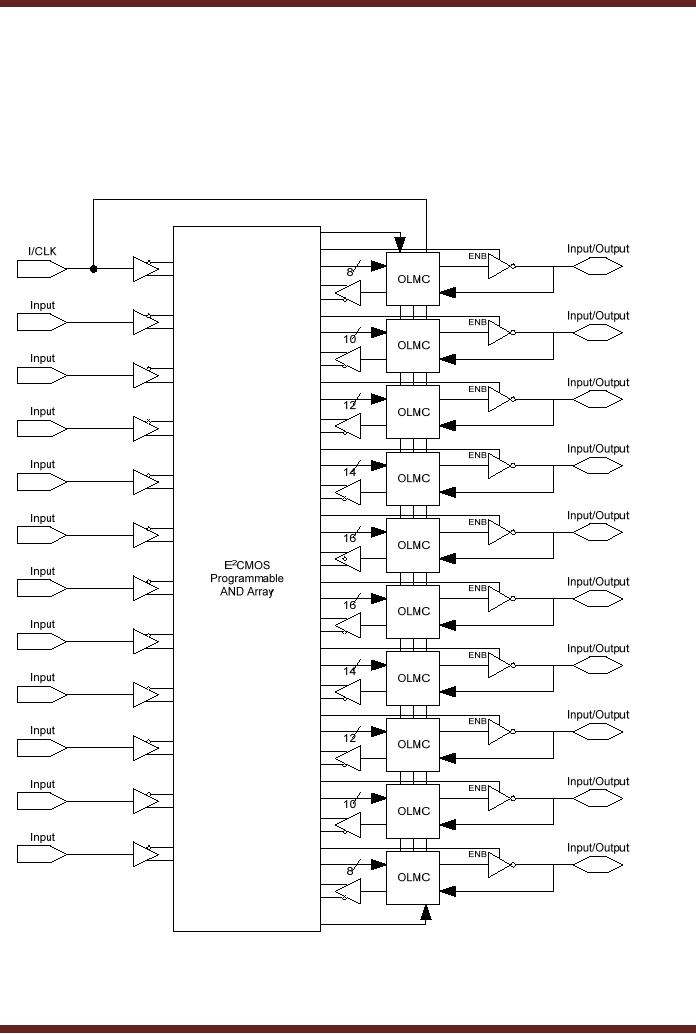
The GAL22V10

The GAL22V10 is a popular GAL device having twelve inputs and ten inputs/outputs.

The device is available as low-voltage 3.3v version. It is also available as an ISP version. The

device has ten OLMCs that can be programmed to different output modes. The ten OLMCs

receive different number of inputs from the programmable AND gate array. Figure 20.7. Of the

ten OLMCs, two have eight inputs, two have ten inputs, two have twelve inputs, two have

fourteen and two have sixteen inputs. Each OLMC can be programmed for active-high, active-

low output or it can be programmed as an input.

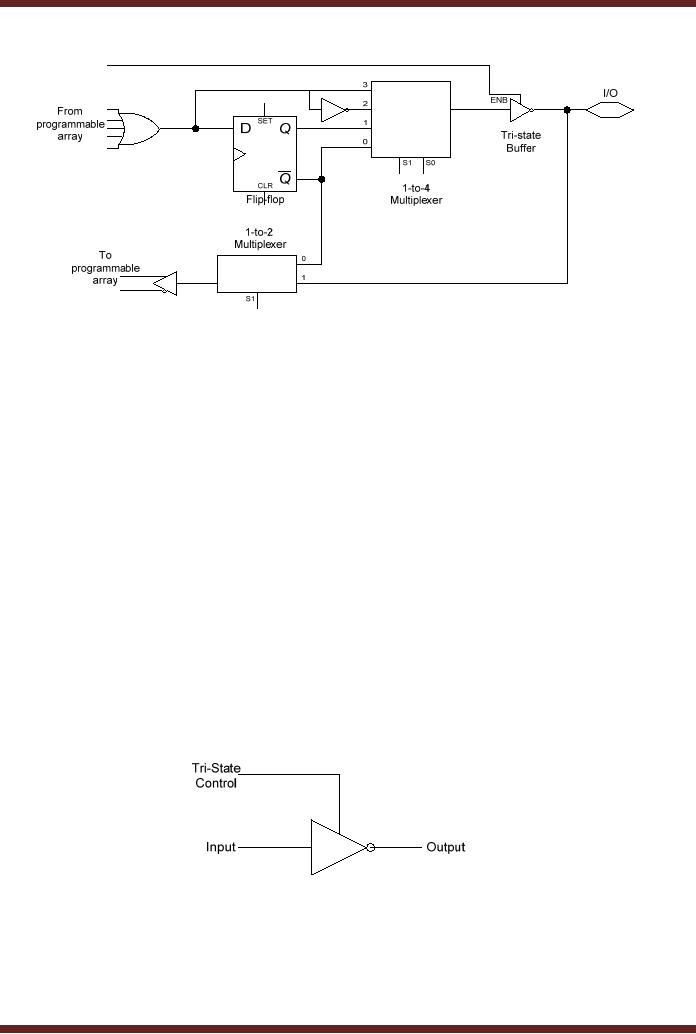
The circuit diagram of an OLMC is shown in figure 20.8. The OLMC consists of a flip-

flop which is a sequential logic device which stores the information at the output of the OR

gate. Flip-flops will be discussed latter. The output and the complemented output of the flip-

flop are connected to the two inputs of the 4-to-1 MUX. The remaining two inputs of the MUX

are connected to the OR gate output and its complemented output. The output of the MUX is

connected to the output through a tri-state buffer. The output is also connected to the input of

194

CS302 - Digital Logic & Design

a 2-to-1 MUX. The other input of the 2-to-1 MUX is connected to the complemented output of

the flip-flop. The output of the 2-to-1 MUX and its complemented output is connected to the

input of the AND array. The select inputs S0 and S1 select the appropriate 4-to-1 MUX input to

be routed to the output or the input. The S1 select input of the 2-to-1 MUX is used to route the

appropriate input to the input of the AND array. The select bits S0 and S1 are programmed in a

dedicated group of cells in the array which are separate from the logic array cells.

Figure 20.7

Block diagram of the GAL22V10

195

CS302 - Digital Logic & Design

Figure 20.8

Circuit Diagram of OLMC

The four OLMC configurations are

· Combination Mode with active-low output

· Combinational Mode with active-high output

· Registered Mode with active-low output

· Registered Mode with active-high output

OLMC Combinational Mode

When the select inputs S0 and S1 are set to 0 and 1 respectively, the 4-to-1 MUX

selects the OR gate output and the output is active-low because of the inversion by the tri-

state buffer. When the select inputs are set to 1 and 1 respectively, the MUX selects the

complement of the OR gate output. The output of the OLMC is active-high due to double

inversion.

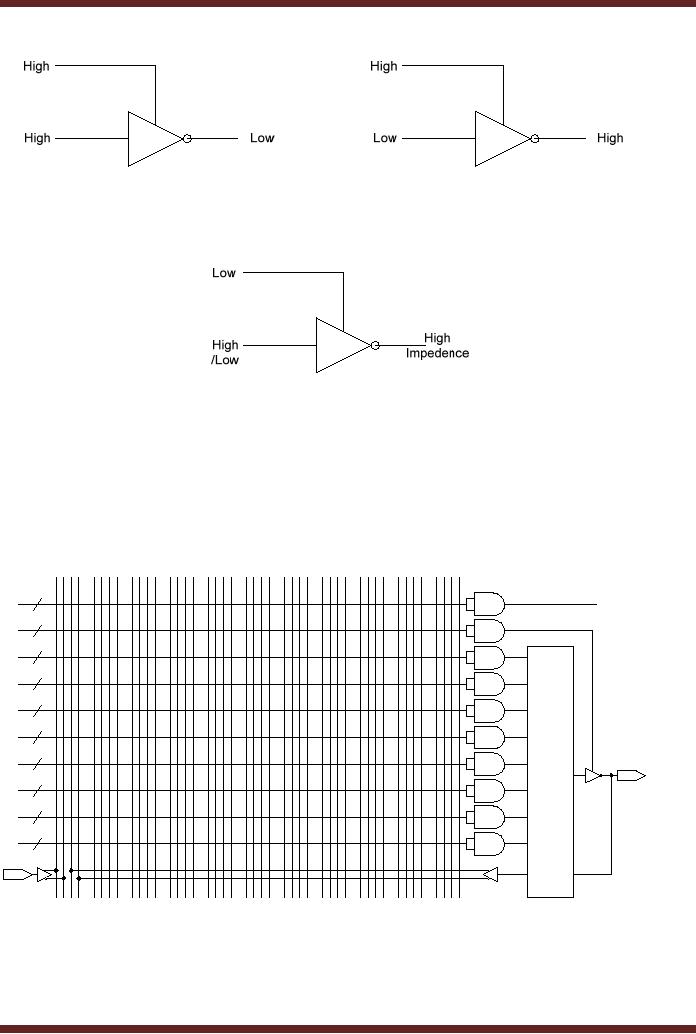
Tri-State Buffers

Tri-State Buffer is a NOT gate with a control line that disconnects the output from the

input. When the control line is high the buffer operates like a NOT gate and when the control

line is low the output is disconnected from the output and high impedance is seen at the

output. Tri-state buffers are used to disconnect the outputs of devices which are connected or

share a common output line. Figure 20.9

Figure 20.9a

Tri-State Buffer

196

CS302 - Digital Logic & Design

Figure 20.9b Tri-State Buffer operating as a NOT gate

Figure 20.9c Tri-State Buffer in High-Impedence State

Referring to the OLMC logic circuit. Figure 20.8. When the control input to the tri-state

buffer is set to low, the output of the buffer is set to high impedance disconnecting the OLMC

from the output pin. The output pin is used as an input pin.

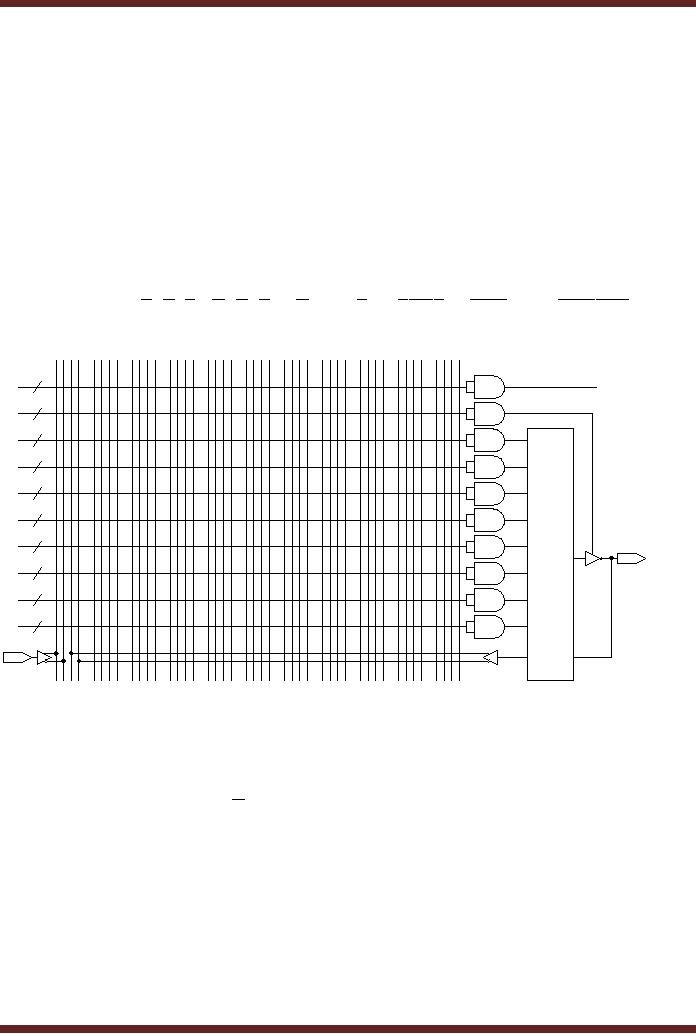
The GAL22V10 Array

Input Lines

Reset to all OLMCs

Input/Output

OLMC

Product Term Lines

Input

Figure 20.10

Detailed Connection to the first OLMC of GAL22V10

The GAL22V10 has 22 inputs organized as 44 lines, one for each input and its

complement. Each AND gate has 44 inputs connected to the 44 input lines. Detailed

197

CS302 - Digital Logic & Design

connection of the first OLMC to the AND array is shown in figure 20.8. The vertical lines in

groups of four represent the inputs. Thus the first group of four vertical lines represents the

input from the GAL input pin and the input from the OLMC. The horizontal lines represent the

product terms. The first OLMC has ten input product terms. Out of the ten product terms, eight

product terms are connected to the OR gate in the first OLMC. Out of the remaining two

product terms, the first product term is used to control the tri-state buffer and the other is used

for reset in the Registered mode for all OLMCs.

Each OLMC ORs the product term to give a single sum of product term. The GAL has

ten such OLMCs therefore a total of ten Sum-of-Product terms can be implemented.

Programming the GAL22V10

Figure 20.11 shown the programmed GAL for the Boolean expression

X = ABCDEF + ABCDEF + ABCDEF + ABCDEF + ABCDEF + ABCDEF + ABCDEF

Input Lines

Reset to all OLMCs

Input/Output

OLMC

Product Term Lines

Input

Figure 20.11

GAL22V10 programmed for Boolean Function

In the figure 20.9 the GAL has been programmed for a six variable Boolean function.

The six variables are connected at the six inputs of the GA device. The figure shows the

connection detail for the first variable A. The first group of four vertical lines represents the

variable A and its complement A . The remaining two lines in the group are not used receive

the un-complemented and complemented output from the OLMC. Similarly, the second group

of four vertical lines are connected to the second input pin of the GAL which is connected to a

signal representing variable B. The next four sets of four vertical lines represent input pins 3,

4, 5 and 6 which are connected to variables C, D, E and F. The Boolean expression that is

implemented has seven product terms. The first OLMC has eight input product terms, thus it

can be used to program the Boolean expression. The output of the first AND gate generates

the first product term of the Boolean expression. Similarly, the 2nd to 7th AND gates generate

the remaining six product terms respectively. The eight input OR gate (not shown) in the

OLMC block generates the sum of product terms. The last group of vertical lines is used to

control the tri-state buffer connected at the output of the OLMC. The diagram shows that it has

198

CS302 - Digital Logic & Design

been set to high to allow the tri-state buffer connect the OLMC output to the output pin of the

GAL.

The GAL16V8

This device has eight inputs and eight inputs/output. The GAL16V8 is designed to be

programmed in one of the three available modes to emulate most of the existing PALs, thus

replacing the PAL. The three modes in which PALs are programmed are

· Simple

· Complex

· Registered

The simple and complex modes are associated with the Combinational Logic whereas the

Registered mode is associated with Sequential Logic.

Simple Mode

In the Simple Mode the OLMC is configured as dedicated active combinational outputs

or as dedicated inputs (limited to six). Three possible combinations of the Simple Mode are

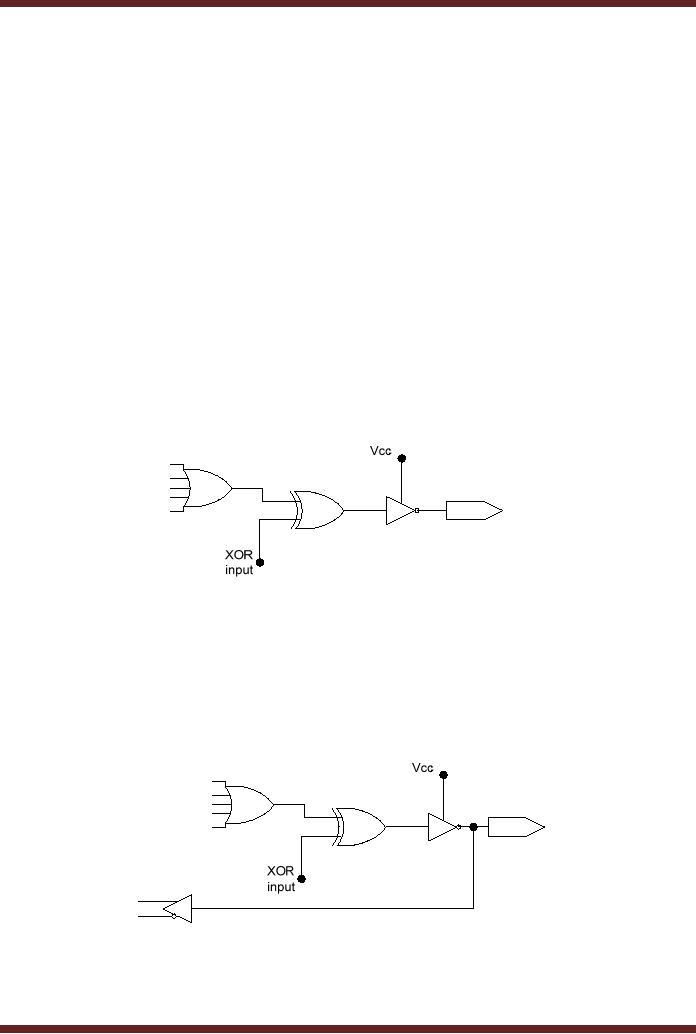
· Combinational Output. Figure 20.12a

· Combinational Output with feedback to AND Array. Fig 20.12b

· Dedicated input. Fig 20.12c

Figure 20.12a Combinational Output

In the Combinational Output the OLMC is configured to give an output which is either active-

low or active-high. The active-state of the output is determined by the XOR input. The tri-state

buffer control pin is set to logic high. The Combinational Output with feedback to AND array is

similar. The tri-state control pin is set to logic high, the XOR gate input determines the active-

state of the output. The signal at the output is also connected to the input of the AND array

through the buffer which provides inverting and non-inverting outputs.

Figure 20.12b Combinational Output with feedback to AND array

199

CS302 - Digital Logic & Design

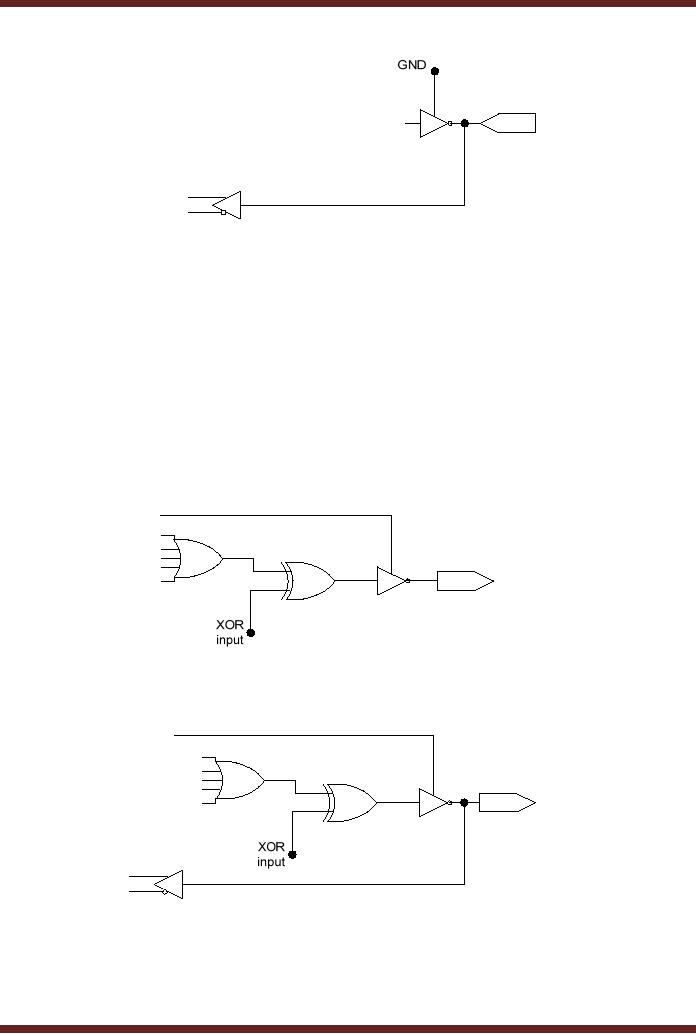
Figure 20.12c Dedicated Input

In the Dedicated Input configuration the tri-state buffer is configured in the high

impedance state by setting the control pin of the tri-state buffer to low. Thus the output pin is

connected t an input signal which is passed to the input of the AND Array in its complemented

and un-complemented form by the buffer.

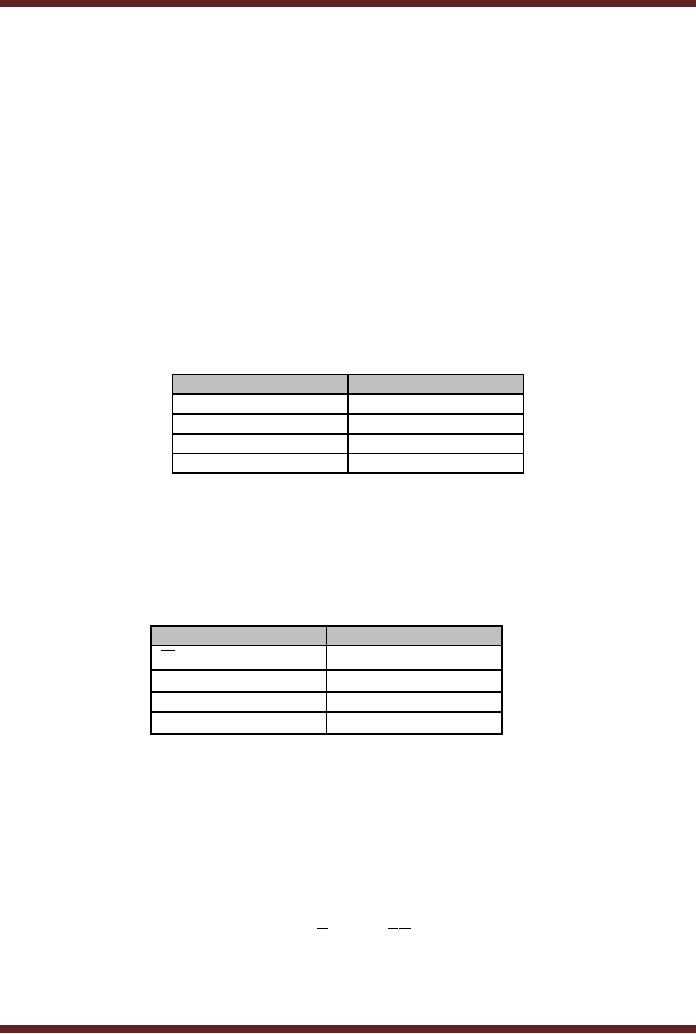
Complex Mode

In this mode the OLMCs can be configured in two ways. In the complex Mode the tri-

state control is formed by a logical expression, this leaves seven product terms that can be

used to form a sum-of product expression.

· Combinational Output. Fig. 20.13

· Combinational Input/Output. Fig. 20.14

Figure 20.13

Combinational Output

Figure 20.14

Combinational Input/Output

Introduction to ABEL

ABEL which is an acronym for Advanced Boolean Expression Language is a hardware

description language used for implementing logic designs using PLDs. ABEL is a device-

200

CS302 - Digital Logic & Design

independent language and can be used to program any type of PLD. ABEL is run on a

computer connected to a PLD programmer which programs the PLD.

ABEL provides three different text-based methods for describing and entering a logic

design. The three methods are

· Boolean Equations

· Truth Tables

· State Diagrams

The Boolean Equations and the Truth Table method are used for Combinational Logic Circuits.

The State Diagram is used specifically for Sequential Logic circuits. The Boolean Equations

and the Truth Table method can also be used for describing and entering Sequential Logic

Circuits.

Boolean Operations

The NOT, AND, OR and XOR operations have special symbols in ABEL as shown in

table 20.1

Logic Operation

ABEL Symbol

NOT

AND

XOR

Table 20.1

ABEL Symbols for logic operations

The standard Boolean notations in terms of ABEL notations are defined in table 20.2

Boolean Notation

ABEL Notation

A.B

A&B

A +B

A#B

A ⊕B

A$B

Table 20.2

Boolean and equivalent ABEL Notations

1. Boolean Equations

One of the ABEL entry methods uses logic equations. In ABEL any letter or

combination of letters and numbers can be used to identify variables. ABEL however is case-

sensitive, thus variable `A' is treated separately from variable `a'. All ABEL equations must end

with `;'. Figure 20.15.

Boolean expression F = AB + AC + BD is written in ABEL as

F = A & !B # A & C # !B & !D;

Figure 20.15 ABEL representation of Boolean expression

201

CS302 - Digital Logic & Design

The operators !, &, # and $ have precedence in the order given in table 20.1

Multiple Inputs and Outputs

In some cases, multiple input and output variables can be grouped as a set to simplify

an equation. Fig 20.16. Thus D0, D1 and D2 input or output variables can be defined by a single

variable D using the ABEL notation D = [D0, D1, D2];

Consider the ABEL description of a 4-input 4-bit Multiplexer. Figure 20.1, Table 20.3

Select Inputs

Outputs

Table 20.3

Truth Table of 4-input 4-bit MUX

The Boolean expressions representing the operation of the MUX are

Y3 = A 3 S1 S 0 + B3 S1S 0 + C3S1 S 0 + D3S1S 0

Y2 = A 2 S1 S 0 + B 2 S1S 0 + C 2S1 S 0 + D 2S1S 0

Y1 = A 1 S1 S 0 + B1 S1S 0 + C1S1 S 0 + D1S1S 0

Y0 = A 0 S1 S 0 + B 0 S1S 0 + C 0S1 S 0 + D 0S1S 0

The ABEL notations representing the operation of the MUX are

Y3 = A3 & !S1 & !S0 # B3 & !S1 & S0 # C3 & S1 & !S0 # D3 & S1 & S0;

Y2 = A2 & !S1 & !S0 # B2 & !S1 & S0 # C2 & S1 & !S0 # D2 & S1 & S0;

Y1 = A1 & !S1 & !S0 # B1 & !S1 & S0 # C1 & S1 & !S0 # D1 & S1 & S0;

Y0 = A0 & !S1 & !S0 # B0 & !S1 & S0 # C0 & S1 & !S0 # D0 & S1 & S0;

The four ABEL notations can be represented by a single notation if variables A3, A2, A1 and

A0 are defined as a set A. Similarly, sets B, C and D can be defined.

A = [A3, A2, A1, A0];

B = [B3, B2, B1, B0];

C = [C3, C2, C1, C0];

D = [D3, D2, D1, D0];

Y = [Y3, Y2, Y1, Y0];

S = [S1, S0];

The ABEL notation representing the MUX is

202

CS302 - Digital Logic & Design

Y = (S = = 0) & A # (S = = 1) & B # (S = = 2) & C # (S = = 3) & D;

The `= =' is a relational operator

Figure 20.16 ABEL representation of multiple inputs and outputs

2. Truth Table

ABEL accepts a logical design described in the form of a Truth Table. Truth Tables are

sometimes more convenient in describing certain logic circuits. The ABEL Truth Table format

includes a header and the truth table entries.

TRUTH_TABLE

( [ A, B, C, D] → [ X1, X2])

A, B, C and D are the inputs and XI and X2 are the outputs.

The truth table of an XOR gate is represented by the ABEL Truth Table notation. Figure 20.17

TRUTH_TABLE

( [A, B] → [X])

[0, 0] → [0];

[0, 1] → [1];

[1, 0] → [1];

[1, 1] → [0];

Figure 20.17 Truth table of an XOR gate

The 2-bit Comparator logic circuit can be described in terms of the truth table using ABEL

notations. Fig 20.18a

TRUTH_TABLE

( [A1, A0, B1, B0] → [G, E, L] )

[0, 0, 0, 0] → [0, 1, 0];

[0, 0, 0, 1] → [0, 0, 1];

[0, 0, 1, 0] → [0, 0, 1];

[0, 0, 1, 1] → [0, 0, 1];

[0, 1, 0, 0] → [1, 0, 0];

[0, 1, 0, 1] → [0, 1, 0];

[0, 1, 1, 0] → [0, 0, 1];

[0, 1, 1, 1] → [0, 0, 1];

[1, 0, 0, 0] → [1, 0, 0];

[1, 0, 0, 1] → [1, 0, 0];

[1, 0, 1, 0] → [0, 1, 0];

[1, 0, 1, 1] → [0, 0, 1];

[1, 1, 0, 0] → [1, 0, 0];

[1, 1, 0, 1] → [1, 0, 0];

[1, 1, 1, 0] → [1, 0, 0];

[1, 1, 1, 1] → [0, 1, 0];

Figure 20.18a

Truth Table of a 2-bit Comparator

203

CS302 - Digital Logic & Design

The ABEL notation can be rewritten by defining a set. Fig 20.18b

INPUT = [A1, A0, B1, B0];

TRUTH_TABLE

( INPUT → [G, E, L] )

0 → [0, 1, 0];

1 → [0, 0, 1];

2 → [0, 0, 1];

3 → [0, 0, 1];

4 → [1, 0, 0];

5 → [0, 1, 0];

6 → [0, 0, 1];

7 → [0, 0, 1];

8 → [1, 0, 0];

9 → [1, 0, 0];

10 → [0, 1, 0];

11 → [0, 0, 1];

12 → [1, 0, 0];

13 → [1, 0, 0];

14 → [1, 0, 0];

15 → [0, 1, 0];

Figure 20.18b

Truth Table of a 2-bit Comparator using a set

Test Vectors

Once the Logic circuit design has been entered its operation can be verified by using

`test vectors'. A `test vector' specifies the inputs and the corresponding outputs. The software

simulates the operation of the logic circuit by applying the test vectors and checking the

outputs.

Test vectors are essentially the same as Truth Tables. Thus the Test Vector for testing

the 2-bit comparator circuit is the same as its truth table. Figure 20.19

TEST_VECTORS

( [A1, A0, B1, B0] → [G, E, L] )

[0, 0, 0, 0] → [0, 1, 0];

[0, 0, 0, 1] → [0, 0, 1];

[0, 0, 1, 0] → [0, 0, 1];

[0, 0, 1, 1] → [0, 0, 1];

[0, 1, 0, 0] → [1, 0, 0];

[0, 1, 0, 1] → [0, 1, 0];

[0, 1, 1, 0] → [0, 0, 1];

[0, 1, 1, 1] → [0, 0, 1];

[1, 0, 0, 0] → [1, 0, 0];

204

CS302 - Digital Logic & Design

[1, 0, 0, 1] → [1, 0, 0];

[1, 0, 1, 0] → [0, 1, 0];

[1, 0, 1, 1] → [0, 0, 1];

[1, 1, 0, 0] → [1, 0, 0];

[1, 1, 0, 1] → [1, 0, 0];

[1, 1, 1, 0] → [1, 0, 0];

[1, 1, 1, 1] → [0, 1, 0];

Figure 20.19a

Test Vector of a 2-bit Comparator

INPUT = [A1, A0, B1, B0];

TEST_VECTORS

( INPUT → [G, E, L] )

0 → [0, 1, 0];

1 → [0, 0, 1];

2 → [0, 0, 1];

3 → [0, 0, 1];

4 → [1, 0, 0];

5 → [0, 1, 0];

6 → [0, 0, 1];

7 → [0, 0, 1];

8 → [1, 0, 0];

9 → [1, 0, 0];

10 → [0, 1, 0];

11 → [0, 0, 1];

12 → [1, 0, 0];

13 → [1, 0, 0];

14 → [1, 0, 0];

15 → [0, 1, 0];

Figure 20.19b

Test Vector of a 2-bit Comparator using a set

The ABEL Input File

When an Input (source) file is created in ABEL a module is created which has three

sections. The three sections are

1. Declarations

The declaration section generally includes the device declaration, pin declarations and

set declarations. Device declaration is used to specify the PLD device that is to be

programmed. The device is referred to as the target device.

Decoder device `P22V10';

The `Decoder' is a description which can be anything defined by the user

The `device' is a reserved keyword which can be in lower or upper case.

The `P22V10' is the device name. It should be in the format shown.

A0, A1, A2, A3, PIN 1, 2, 3, 4;

`PIN" is a keyword which can be in lower or upper case.

205

CS302 - Digital Logic & Design

Pin declaration defines the relationship between the variables and the corresponding pin

numbers of the PLD.

INPUT = [A1, A0, B1, B0];

`INPUT' defines a set made up of set elements A1, A0, B1 and B0. In subsequent ABEL

notations the set `INPUT' can be used instead of set variables.

2. Logic Descriptions

Logic descriptions include the three methods of describing a logic circuit. Two methods

the Boolean equation and the Truth Table method already have been discussed.

3. Test Vectors

The Test Vector format has been described. The Test vector description is used to

simulate the logic circuit and verify its operation.

The example describes the Input (source) file for a 2-bit Comparator logic circuit.

The Documentation file

After an input file is processed by ABEL a documentation file is generated which

provides a hardcopy of the final reduced equations and a device pin diagram.

206

Table of Contents: