 |
Binary to Decimal to Binary conversion, Binary Arithmetic, 1’s & 2’s complement |
| << AN OVERVIEW & NUMBER SYSTEMS |
| Range of Numbers and Overflow, Floating-Point, Hexadecimal Numbers >> |

CS302 -
Digital Logic & Design
Lesson
No. 02
NUMBER
SYSTEMS
Binary to
Decimal conversion
Most
real world quantities are
represented in Decimal Number
System. Digital
Systems
on the
other hand are based on
the Binary Number System.
Therefore, when converting
from
the
Digital Domain to the
real-world, Binary numbers
have to be represented in terms of
their
Decimal
equivalents.
The
method used to convert from
Binary to Decimal is the
Sum-of-Weights method.
The
Sum-of-Weights method has
been used to represent the
Caveman numbers Ć↑, ĆΩ↑∑
and
the Binary numbers 10011
and 1011.101 in the first
lecture.
1. Sum-of-Weights
Method
Sum-of-weights
as the name indicates sums
the weights of the Binary
Digits (bits) of a
Binary
Number which is to be represented in
Decimal. The Sum-of-Weights
method can be
used to
convert a Binary number of
any magnitude to its
equivalent Decimal
representation.
In the
Sum-of-Weights method an extended
expression is written in terms of
the Binary
Base
Number 2 and the weights of
the Binary number to be
converted. The
weights
correspond to
each of the binary bits
which are multiplied by the
corresponding binary
value.
Binary
bits having the value 0 do
not contribute any value
towards the final sum
expression.
The
Binary number 101102 is therefore written in the
form of an expression
having
weights
20, 21, 22, 23 and 24 corresponding to the bits 0,
1, 1, 0 and 1 respectively. Weights
20
and
23 do not contribute
in the final sum as the
binary bits corresponding to
these weights
have
the value 0.
= 1 x 24 + 0 x 23 + 1 x 22 + 1 x
21 + 0 x 20
101102
= 16 + 0 + 4 + 2 +
0
= 22
2. Sum-of-non-zero
terms
In the
Sum-of-Weights method, the
Binary bits 0 do not
contribute towards the
final
sum
representing the decimal
equivalent. Secondly, the
weight of each binary bit
increases by
a factor of 2
starting with a weight of 1
for the least significant
bit. For example, the
Binary
number
101102 has weights
20=1, 21=2, 22=4,
23=8 and 24=16 corresponding to the
bits 0, 1,
1, 0 and 1
respectively.
The
Sum-of-non-zero terms method is a
quicker method to determine
decimal
equivalents of
binary numbers without
resorting to writing an expression. In
the Sum-of-non-
zero
terms method the weights of
non-zero binary bits are
summed, as the weights of
zero
binary
bits do not contribute
towards the final sum
representing the decimal
equivalent.
The
weights of binary bits
starting from the right
most least significant bit
is 1, The next
significant
bit on the left has
the weight 2, followed by 4, 8,
16, 32 etc. corresponding to
higher
significant
bits. In binary number
system the weights of
successive bits increase by an
order of
2 towards
the left side and
decrease by an order of 2 towards
the right side. Thus a
binary
number
can be quickly converted
into its decimal equivalent
by adding weights of
non-zero
terms
which increase by a factor of 2.
Binary numbers having an
integer and a fraction
part
can
similarly be converted into
their decimal equivalents by
applying the same
method.
14
CS302 -
Digital Logic & Design
A quicker
method is to add the weights
of non-zero terms. Thus for
the numbers
o 100112 = 16 + 2 + 1 = 19
o 1011.1012 = 8 + 2 + 1 + � + 1/8 = 11 + 5/8 =
11.625
Decimal to
Binary conversion
Conversion
from Decimal to Binary
number system is also
essential to represent
real-world
quantities in
terms of Binary values. The
Sum-of-weights and repeated
division by 2 methods
are
used to convert a Decimal
number to equivalent
Binary.
1.
Sum-of-Weights
The
Sum-of-weights method used to
convert Binary numbers into
their Decimal
equivalent is
based on adding binary
weights of the binary number
bits. Converting back
from
the
decimal number to the
original Binary number
requires finding the highest
weight included
in the
sum representing the decimal
equivalent. A Binary 1 is marked to
represent the bit
which
contributed its weight in
the Sum representing the
decimal equivalent. The
weight is
subtracted
from the sum decimal
equivalent. The next highest
weight included in the sum
term
is found. A
binary 1 is marked to represent
the bit which contributed
its weight in the sum
term
and
the weight is subtracted
from the sum term.
This process is repeated
until the sum
term
becomes
equal to zero. The binary 1s
and 0s represent the binary
bits that contributed
their
weight
and bits that did
not contribute any weight
respectively.
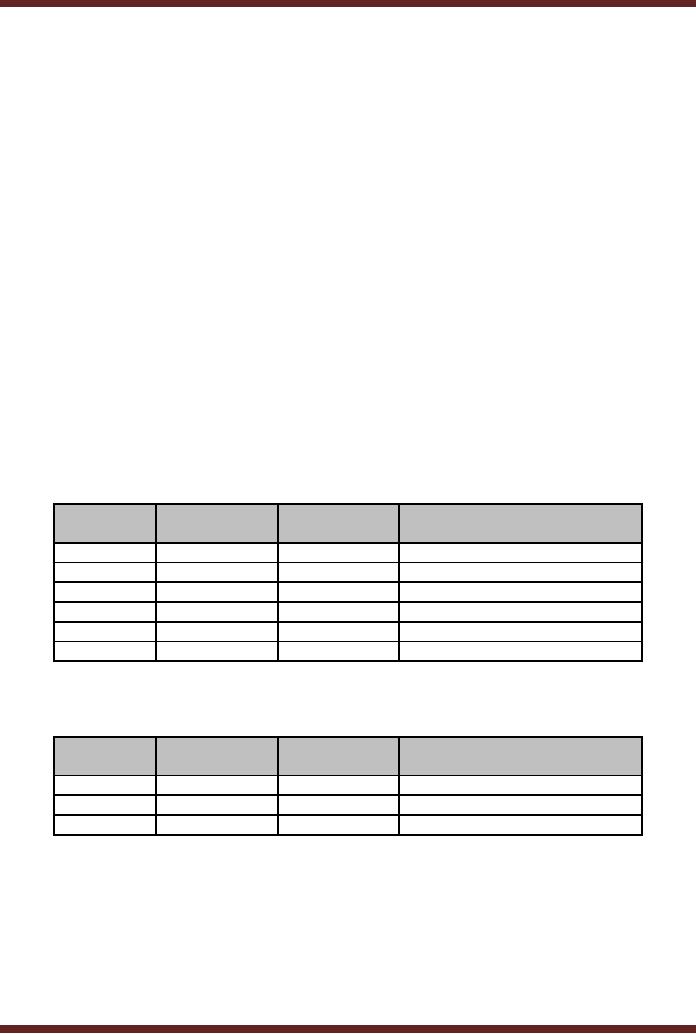
The
process of determining Binary
equivalent of a Decimal number
392 and 411 is
illustrated in a
tabular form. Table
2.1.
Sum
Term
Highest
Binary
Sum
Term
Weight
Number
= Sum
Term Highest
Weight
411
256
100000000
155
155
128
110000000
27
27
16
110010000
11
11
8
110011000
3
3
2
110011010
1
1
1
110011011
0
Table
2.1a
Converting
Decimal to Binary using
Sum-of-Weights Method
Sum
Term
Highest
Binary
Sum
Term
Weight
Number
= Sum
Term Highest
Weight
392
256
100000000
136
136
128
110000000
8
8
8
110001000
0
Table
2.1b
Converting
Decimal to Binary using
Sum-of-Weights Method
The
Sum of weights method
requires mental arithmetic
and is a quick way of
converting
small decimal numbers into
binary. With practice large
Decimal numbers can
be
converted
into Binary
equivalents.
2. Repeated
Division-by-2
Repeated
Division-by-2 method allows
decimal numbers of any
magnitude to be
converted
into binary. In this method
the Decimal number to be
converted into its
Binary
15
CS302 -
Digital Logic & Design
equivalent is
repeatedly divided by 2. The
divisor is selected as 2 because
the decimal number
is being
converted into Binary a
Base-2 Number system.
Repeated division method can
be
used to
convert decimal number into
any Number system by
repeated division by the
Base-
Number.
For example, the decimal
number can be converted into
the Caveman Number
system by
repeatedly dividing by 5, the
Base number of the Caveman
Number System. The
Repeated
Division method will be used
in latter lectures to convert
decimal into
Hexadecimal
and
Octal Number Systems.
In the
Repeated-Division method the
Decimal number to be converted is
divided by the
Base
Number, in this particular
case 2. A quotient value and
a remainder value is
generated,
both
values are noted done.
The remainder value in all
subsequent divisions would be
either a
0 or a 1. The
quotient value obtained as a
result of division by 2 is divided
again by 2. The new
quotient
and remainder values are
again noted down. In each
step of the repeated
division
method
the remainder values are
noted down and the
quotient values are
repeatedly divided
by the
base number. The process of
repeated division stops when
the quotient value
becomes
zero.
The remainders that have
been noted in consecutive
steps are written out to
indicate the
Binary
equivalent of the Original
Decimal Number.
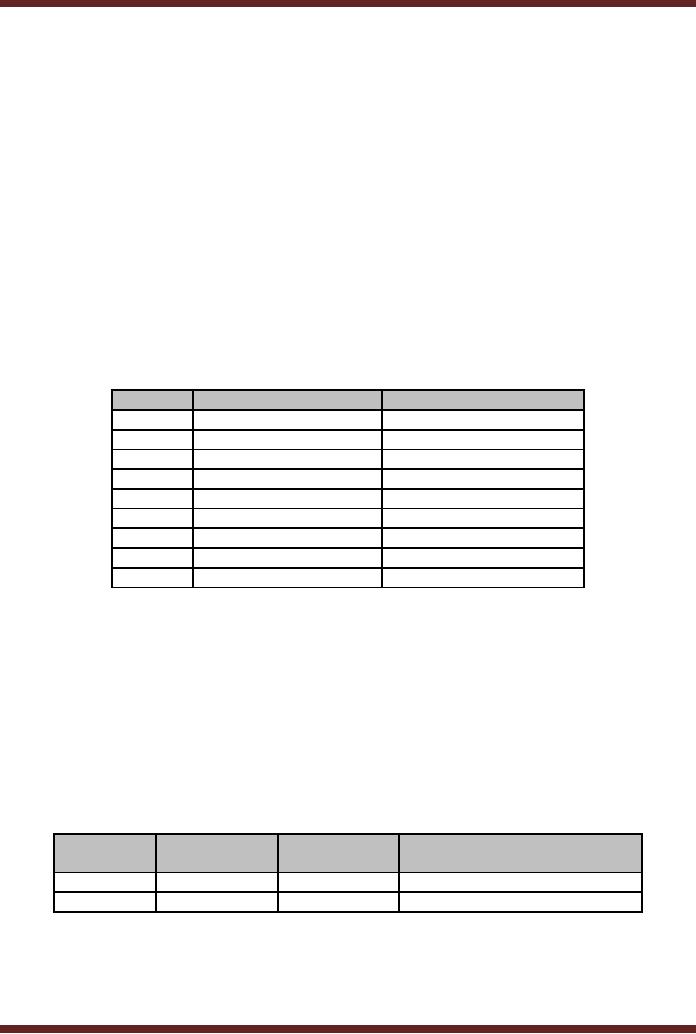
Number
Quotient
after division
Remainder
after division
392
196
0
196
98
0
98
49
0
49
24
1
24
12
0
12
6
0
6
3
0
3
1
1
1
0
1
Table
2.2
Converting
Decimal to Binary using
Repeated Division by 2
Method
The
process of determining the
Binary equivalent of a Decimal
number 392 is
illustrated in a
tabular form. Table 2.2.
Reading the numbers in the
Remainder column from
bottom to
top 110001000 gives the
binary equivalent of the
decimal number 392
Converting
Decimal fractions to
Binary
Two
methods are used to Convert
Decimal fractions to Binary.
The Sum-of-Weights
method,
which has been described
and used to convert Decimal
Integers into Binary
Equivalents is
applied to convert Decimal
fractions into Binary
fractions. This method
requires
mental
arithmetic and is suitable
for small numbers. The
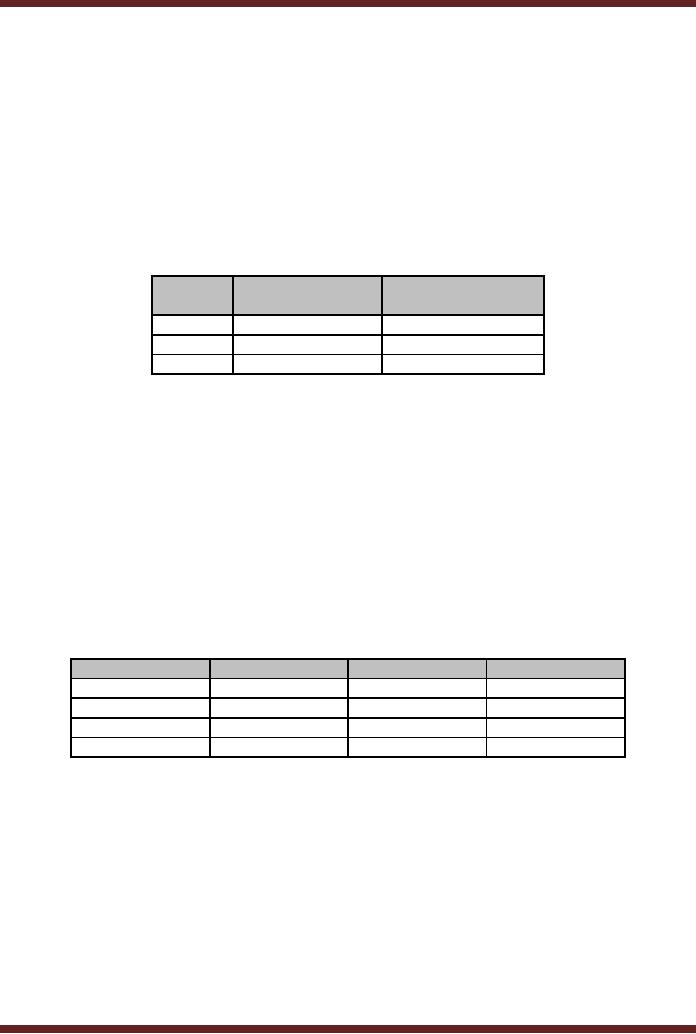
conversion of Decimal fraction
0.625
into
Binary equivalent is illustrated in a
tabular form. Table
2.3
Sum
Term
Highest
Binary
Sum
Term
Weight
Number
= Sum
Term Highest
Weight
0.625
0.500
0.100
0.125
0.125
0.125
0.101
0
Table
2.3
Converting
Decimal to Binary using
Sum-of-Weights Method
Repeated
Multiplication-by-2 Method
An alternate to
the Sum-of-Weights method
used to convert Decimal
fractions to
equivalent
Binary fractions is the
repeated multiplication by 2 method. In
this method the
16
CS302 -
Digital Logic & Design
number to be
converted is repeatedly multiplied by
the Base Number to which
the number is
being
converted to, in this case
2. A new number having an
Integer part and a Fraction
part is
generated
after each multiplication.
The Integer part is noted
down and the fraction
part is
again
multiplied with the Base
number 2. The process is
repeated until the fraction
term
becomes
equal to zero.
Repeated
Multiplication-by-2 method allows
decimal fractions of any
magnitude to be easily
converted
into binary. The conversion
of Decimal fraction 0.625
into Binary equivalent
using
the
Repeated Multiplication-by-2 method is
illustrated in a tabular form.
Table 2.4. Reading
the
Integer
column from bottom to top
and placing a decimal point
in the left most position
gives
0.101
the binary equivalent of
decimal fraction
0.625
Number
Integer
part after
Fraction
part after
multiplication
multiplication
0.625
1
0.25
0.25
0
0.5
0.5
1
0.0
Table
2.4 Converting Decimal to
Binary using repeated
Multiplication-by-2 Method
Binary
Arithmetic
Digital
systems use the Binary
number system to represent
numbers. Therefore
these
systems
should be capable of performing
standard arithmetic operations on
binary numbers.
1. Binary
Addition
Binary
Addition is identical to Decimal
Addition. By adding two
binary bits a Sum
bit
and a
Carry bit are generated.
The only difference between
the two additions is the
range of
numbers
used. In Binary Addition,
four possibilities exist
when two single bits
are added
together.
The four possible input
combinations of two single
bit binary numbers and
their
corresponding
Sum and Carry Outputs
are specified in table
2.5.
First
Number
Second
Number
Sum
Carry
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
Table
2.5
Addition of
two Single Bit Binary
Numbers
The
first three additions give a
result 0, 1 and 1 respectively
which can be
represented
by a single
binary digit (bit). The
fourth addition results in
the number 2, which can
be
represented in
binary as 102.
Thus two digits (bits)
are required. This is
similar to the
addition
of 9 + 3 in
decimal. The answer is 12
which can not be represented
by a single digit, thus
two
digits
are required. The number 2
is the sum part and 1 is
the carry part.
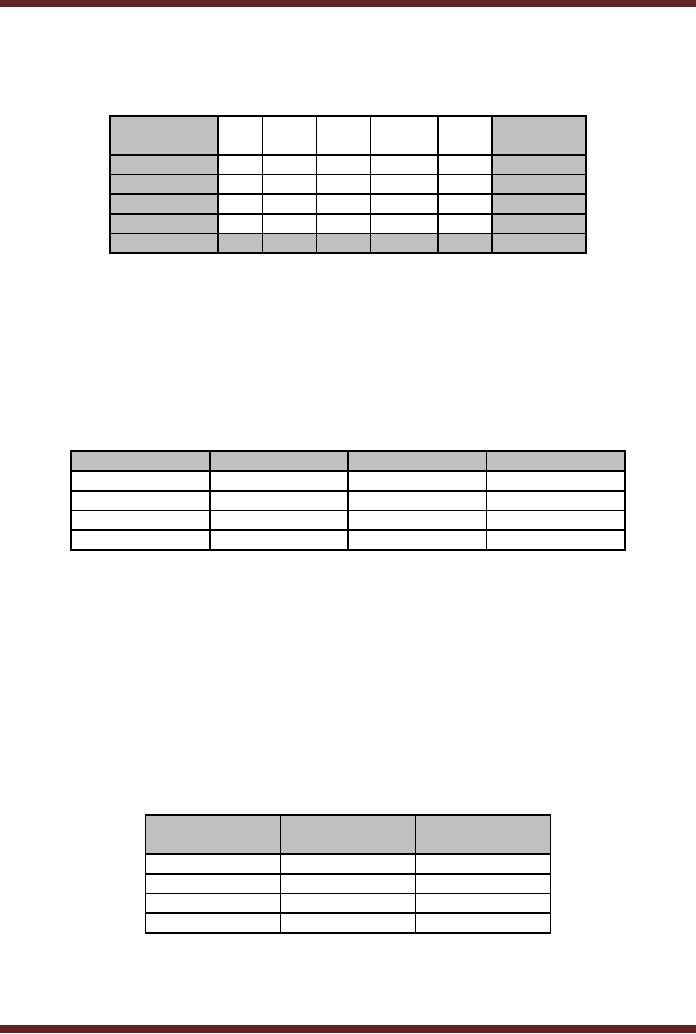
Any number of
binary numbers having any
number of digits can be
added together.
Thus
the number 1011, 110,
1000 and 11 can be added
together. Most significant
digits (bits)
of second
and fourth numbers are
assumed to be zero.
17
CS302 -
Digital Logic & Design
Carry
1
10
1
Decimal
Equivalent
1st Number
1
0
1
1
(11)
2nd Number
1
1
0
(06)
3rd Number
1
0
0
0
(08)
4th Number
1
1
(03)
Result
1
1
1
0
0
(28)
Table
2.6
Adding
multiple binary numbers of
different sizes
2. Binary
Subtraction
Binary
Subtraction is identical to Decimal
Subtraction. The only
difference between
the
two is
the range of numbers.
Subtracting two single bit
binary numbers results in a
difference
bit
and a borrow bit. The
four possible input
combinations of two single
bit binary numbers
and
their
corresponding Difference and
Borrow Outputs are specified
in table 2.7. It is
assumed
that
the second number is
subtracted from the first
number.
First
Number
Second
Number
Difference
Borrow
0
0
0
0
0
1
1
1
1
0
1
0
1
1
0
0
Table
2.7
Subtraction of
two Single Bit Binary
Numbers
The
second subtraction subtracts 1
from 0 for which a Borrow is
required to make the
first
digit equal to 2. The
Difference is 1. This is similar to
decimal subtraction when 17
is
subtracted
from 21. The first
digit 7 can not be
subtracted from 1, therefore 10 is
borrowed
from
the next significant digit.
Borrowing a 10 allows subtraction of 7
from 11 resulting in a
Difference of
4.
3. Binary
Multiplication
Binary
Multiplication is similar to the
Decimal multiplication except
for the range of
numbers.
Four possible combinations of
two single bit binary
numbers and their products
are
listed in
table 2.8.
First
Number
Second
Product
Number
0
0
0
0
1
0
1
0
0
1
1
1
Table
2.8
Multiplication
of two Single Bit Binary
Numbers
Multiplying
two binary numbers such as
1101 x 101 is performed by a
shift and add
operation.
The binary multiplication
shifts and adds partial
product terms.
18
CS302 -
Digital Logic & Design
1101
x
101
1101
1st product
term
2nd product term
0000
3rd product term
1101
1000001
4. Binary
Multiplication by shifting
left
Binary
Multiplication can be performed by
shifting the binary number
towards left. A left
shift by a
single bit is equivalent to
multiplication by 2. A left shift by
two bits is equivalent
to
multiplication
by 4. Generally, the multiplication
factor is determined by 2n where n is the
number of
bit shifts.
00011
(3)
original
binary number
00110
(6)
binary
number shifted left by 1
bit
01100
(12)
binary
number shifted left by 2
bits
11000
(24)
binary
number shifted left by 3
bits
5. Binary
Division
Division in
binary follows the same
procedure as in the division of
decimal numbers. An
example
illustrates the division of
binary numbers. Figure
2.1.
10
101 |
1101
101
011
000
11
Figure
2.1
Binary
Division
6. Binary
Division by Shifting
right
Binary
Division can be performed by
shifting the binary number
towards right. A
right
shift by a
single bit is equivalent to
division by 2. A right shift by
two bits is equivalent
to
division by 4.
Generally, the division
factor is determined by 2n where n is the number of
bit
shifts.
10100
(20)
original
binary number
01010
(10)
binary
number shifted right by 1
bit
00101
(5)
binary
number shifted right by 2
bits
Signed
and Unsigned Binary
Numbers
Digital
systems not only handle
positive numbers but both
positive and negative
numbers. In
the decimal number system
positive numbers are
identified by the + sign
and
negative
numbers are represented by
the sign.
In a digital
system which uses the
Binary number system, the
positive and negative
signs
can not be represented as +
and -. As mentioned in the
Overview all forms of
numbers,
text,
punctuation marks etc. are
represented in the form of 1s
and 0s. Thus the
positive and
negative
signs are also presented in
terms of binary 0 and
1.
19
CS302 -
Digital Logic & Design
To handle
positive and negative binary
numbers, the digital system
sets aside the
most
significant
digit (bit) to represent the
sign
� MSB set to
1 indicates a negative
number
� MSB set to
0 indicates a positive
number
Thus
+13 and -13 are
represented as 01101and 11101
respectively. The bits
1101
represent
the number 13 and the
MSBs 0 and 1 represent
positive and negative
signs
respectively.
Thus binary numbers having
the MSB signifying the Sign
bit are treated as
Signed
Binary Numbers. This
representation is known as
the Signed-Magnitude
representation.
Digital
systems also handle binary
numbers which are assumed to
be positive and
therefore do
not have the most
significant sign bit. Such
numbers are known as
Unsigned
numbers.
Digital system thus have to
handle two different types
of binary numbers, signed
and
unsigned.
Thus 111012 represents -13 in signed
binary and 29 in unsigned
binary. How should
a Digital
System treat a binary
number? Should it consider it as a
signed or unsigned
number?
A digital
system on its own can
not decide how to handle a
binary number. The digital
system
has to be
notified beforehand to deal
with a certain binary
representation as signed or
unsigned.
1's &
2's complement
Informing
the digital system how to
treat a binary number is not
very efficient. A
better
way is to
represent negative signed
numbers in their 2's
complement form. Using
2's
Complement
form to represent signed
numbers, allows direct
manipulation of positive as
well
as negative
numbers without having to
worry about setting the
most significant sign bit
to
indicate
positive and negative
numbers.
A 2's
complement of a number is obtained by
first taking the 1's
complement of a
number
and then adding a 1 to
change the 1's complement to
2's complement. 1's
complement of a
number is obtained by simply
inverting all its bits.
Obtaining the 2's
complement of 13
is described in the example
below.
01101
The
number 13
10010
1's
complement of 13 is obtained by inverting
all the five
bits.
+
1
10011
2's
complement of 13 is obtained by adding a
1 to its 1's
complement.
In a 2's
complement number system all
negative numbers are
represented in their
2's
complement
form and all positive
numbers are represented in
their actual form.
Negative
numbers
can be readily identified by
their MSBs which are
set to 1. Thus in a 2's
complement
representation
+13 is represented as 01101
and -13 is represented as
10011.
By having
numbers represented in their
2's complement form addition
and subtraction
operations
can easily be performed
without having to worry
about the sign bits.
Thus +13
added to
-13 should result in a zero
value. This can be verified
by directly adding the +13
and -
13 in their
2's complement forms.
01101
10011
100000
20

CS302 -
Digital Logic & Design
The
most significant carry bit
is discarded; retaining only
the first 5 bits proves
that
adding
+13 and -13 results in a
zero value. Similarly it can
be shown that adding the
numbers
+7 and
-13 results in -6.
10011
(-13)
00111
(+7)
11010
(-6)
The
binary 2's complement number
11010 has its most
significant bit set to 1
indicating
that
the number is negative. The
actual magnitude of the
negative number is determined
by
taking
the 2's complement of
11010.
11010
Original
number
00101
1's
complement of Original
number
+1
00110
2's
complement of Original number is
equal to 6.
Addition
and Subtraction Operations
with Signed
Binary
An additional
benefit of using 2's
complement representation for
signed numbers is
that
both
add and subtract operations
can be performed by addition. In
the above example 13
was
subtracted
from 7 by adding 2's
complement of -13 to 2's
complement of +7. Four cases
of
adding
and subtracting numbers
using the 2's complement
representation are shown
below.
�
Both
numbers are positive
0101
+5
0010
+2
0111
+7
�
Both
numbers are negative
1011
-5
1110
-2
11001
-7
the
carry generated from the
msb is discarded
�
One
number is positive and its
magnitude is larger than the
negative number
0101
+5
1110
-2
10011
+3
the
carry generated from the
msb is discarded
�
One
number is positive and its
magnitude is smaller than
the negative number
1011
-5
0010
+2
1101
-3
The
four examples show that
add and subtract operations
can be carried out by
an
adder
circuit if numbers are
represented in their 2's
complement form. A separate
circuit to
perform
subtractions is not
required.
Range of
Signed and Unsigned Binary
numbers
Three
different types of Binary
representations have been
discussed. The
Unsigned
Binary
representation can only
represent positive binary
numbers. The Sign-Magnitude
can
21
CS302 -
Digital Logic & Design
represent
both positive and negative
numbers. The 2's complement
signed representation
also
allows
positive and negative
numbers to be handled.
Each of
the three binary number
representations can represent
certain range of
binary
numbers
determined by the total
number of bits used.
The
maximum range of values that
can be represented in any
number system depends
upon
the number of digits
assigned to represent the
value. A 5-digit car
odometer can only
count up to
99,999 and then it rolls
back to 00000. Similarly an
8-digit calculator can
only
handle
integer numbers of the
magnitude 99,999,999. A calculator
that reserves the
most
significant
digit to write + or can
only handle a maximum range
of integer numbers from
-
9,999,999 to
+9,999,999.
A 3-bit
unsigned binary number can
have values ranging between
000 and 111.
Adding
100
and 111 unsigned numbers
results in 1011, this result
is considered to be out of range
as
4 bits
are required. Similarly a
4-bit sign magnitude number
can handle a number
range
between -7
and +7. -8 can not be
represented as 5-bits are
required 11000. A 4-bit
2's
complement
based signed number range is
between -8 to +7.
The
table 2.9 shows the
range of values that can be
represented by the three
Binary
representations
using 4-bits.
Decimal
Sign-Magnitude
2's
complement
Unsigned
form
Number
form
form
-8
1000
-7
1111
1001
-6
1110
1010
-5
1101
1011
-4
1100
1100
-3
1011
1101
-2
1010
1110
-1
1001
1111
0
0000
0000
000
1
0001
0001
001
2
0010
0010
010
3
0011
0011
011
4
0100
0100
100
5
0101
0101
101
6
0110
0110
110
7
0111
0111
111
Table
2.9
Range of
values represented by 4-bit
Binary representations
�
Signed
Magnitude representation can
represent positive and
negative numbers in
the
range
(2n-1-1) and
-(2n-1-1) where n represents
the number of bits.
�
2's
complement signed representation
can represent positive and
negative numbers in
the
range
(2n-1-1) and
-(2n-1)
where n represents the
number of bits.
The
unsigned representation can
represent positive numbers in
the range 0 to 2n-1,
where
�
n represents
the number of bits.
22
Table of Contents:
- AN OVERVIEW & NUMBER SYSTEMS
- Binary to Decimal to Binary conversion, Binary Arithmetic, 1’s & 2’s complement
- Range of Numbers and Overflow, Floating-Point, Hexadecimal Numbers
- Octal Numbers, Octal to Binary Decimal to Octal Conversion
- LOGIC GATES: AND Gate, OR Gate, NOT Gate, NAND Gate
- AND OR NAND XOR XNOR Gate Implementation and Applications
- DC Supply Voltage, TTL Logic Levels, Noise Margin, Power Dissipation
- Boolean Addition, Multiplication, Commutative Law, Associative Law, Distributive Law, Demorgan’s Theorems
- Simplification of Boolean Expression, Standard POS form, Minterms and Maxterms
- KARNAUGH MAP, Mapping a non-standard SOP Expression
- Converting between POS and SOP using the K-map
- COMPARATOR: Quine-McCluskey Simplification Method
- ODD-PRIME NUMBER DETECTOR, Combinational Circuit Implementation
- IMPLEMENTATION OF AN ODD-PARITY GENERATOR CIRCUIT
- BCD ADDER: 2-digit BCD Adder, A 4-bit Adder Subtracter Unit
- 16-BIT ALU, MSI 4-bit Comparator, Decoders
- BCD to 7-Segment Decoder, Decimal-to-BCD Encoder
- 2-INPUT 4-BIT MULTIPLEXER, 8, 16-Input Multiplexer, Logic Function Generator
- Applications of Demultiplexer, PROM, PLA, PAL, GAL
- OLMC Combinational Mode, Tri-State Buffers, The GAL16V8, Introduction to ABEL
- OLMC for GAL16V8, Tri-state Buffer and OLMC output pin
- Implementation of Quad MUX, Latches and Flip-Flops
- APPLICATION OF S-R LATCH, Edge-Triggered D Flip-Flop, J-K Flip-flop
- Data Storage using D-flip-flop, Synchronizing Asynchronous inputs using D flip-flop
- Dual Positive-Edge triggered D flip-flop, J-K flip-flop, Master-Slave Flip-Flops
- THE 555 TIMER: Race Conditions, Asynchronous, Ripple Counters
- Down Counter with truncated sequence, 4-bit Synchronous Decade Counter
- Mod-n Synchronous Counter, Cascading Counters, Up-Down Counter
- Integrated Circuit Up Down Decade Counter Design and Applications
- DIGITAL CLOCK: Clocked Synchronous State Machines
- NEXT-STATE TABLE: Flip-flop Transition Table, Karnaugh Maps
- D FLIP-FLOP BASED IMPLEMENTATION
- Moore Machine State Diagram, Mealy Machine State Diagram, Karnaugh Maps
- SHIFT REGISTERS: Serial In/Shift Left,Right/Serial Out Operation
- APPLICATIONS OF SHIFT REGISTERS: Serial-to-Parallel Converter
- Elevator Control System: Elevator State Diagram, State Table, Input and Output Signals, Input Latches
- Traffic Signal Control System: Switching of Traffic Lights, Inputs and Outputs, State Machine
- Traffic Signal Control System: EQUATION DEFINITION
- Memory Organization, Capacity, Density, Signals and Basic Operations, Read, Write, Address, data Signals
- Memory Read, Write Cycle, Synchronous Burst SRAM, Dynamic RAM
- Burst, Distributed Refresh, Types of DRAMs, ROM Read-Only Memory, Mask ROM
- First In-First Out (FIFO) Memory
- LAST IN-FIRST OUT (LIFO) MEMORY
- THE LOGIC BLOCK: Analogue to Digital Conversion, Logic Element, Look-Up Table
- SUCCESSIVE –APPROXIMATION ANALOGUE TO DIGITAL CONVERTER