16-BIT ALU, MSI 4-bit Comparator, Decoders

<< BCD ADDER: 2-digit BCD Adder, A 4-bit Adder Subtracter Unit

BCD to 7-Segment Decoder, Decimal-to-BCD Encoder >>

CS302 - Digital Logic & Design

Lesson No. 16

16-BIT ALU

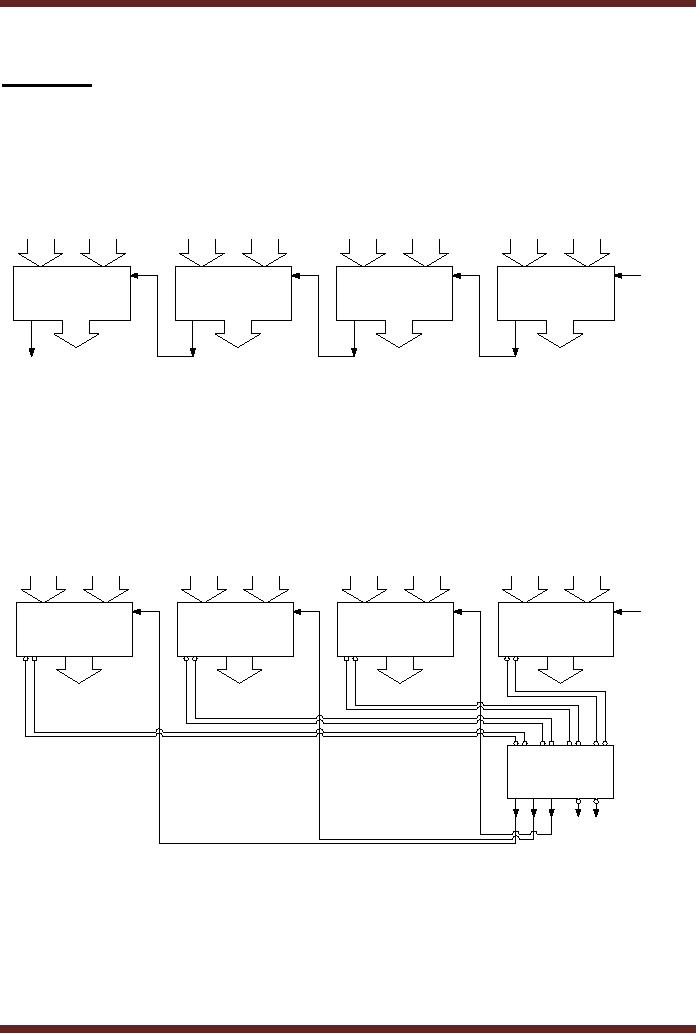
Consider the four ALUs connected to form a 16-bit ALU without the Look-Ahead Carry

circuit. Figure 16.1. The ALU1 will only generate an output and a Carry Out 8 when it has

received an input at Carry In 4. Similarly, ALU2 will only generate an output and a Carry Out

12 when it has received Carry In 8. Finally, the Carry Out 16 is generated only when ALU3 has

received Carry In 12. Thus the Carry instead of rippling through the 4-bits of the individual ALU

circuit has to propagate through four ALU units. The last ALU unit has to wait until it receives

the Carry propagating through each of the three units.

Cin8

Cin4

Cin0

Cin12

ALU3

ALU2

ALU1

ALU0

Cout16

Cout12

Cout8

Cout4

Figure 16.1

Carry Propagation Delay between 4-bit ALU units

The delay caused by the Carry Propagating through the four units is eliminated by the

Group Carry terms used by the 381 ALUs. Figure 16.2. Instead of the Carry Out each ALU

generates Group-Carry Generate and Propagate terms, which indicate if the most significant

Carry is generated by the 4-bit ALU or otherwise. The Group Carry terms are connected to the

Look-Ahead Carry Generator which generates the Cary bits C1, C2 and C3 which are

connected to Cin4, Cin8 and Cin12 respectively. Thus Carry no longer propagates through the

ALU units.

Cin8

Cin4

Cin0

Cin12

ALU3

ALU2

ALU1

ALU0

G3 P3 G2 P2 G1 P1 G0 P0

Look-Ahead

Carry Generator

Figure 16.2

Carry Propagation Delay eliminated by using Group Carry

The G output is activated if the 4-bit unit generates a Carry Out irrespective of Carry In.

The P output is activated if the 4-bit unit generates a Carry Out if the Carry In is active. The

Look-Ahead circuit implemented earlier is based on Logic Gates, where the Look-Ahead Carry

150

CS302 - Digital Logic & Design

Generator circuit has P0, P1, P2 and P3 Carry Propagate and G0, G1, G2 and G3 Carry

Propagate Inputs and C1, C2, C3 and C4 Carry Out outputs. The 74XX182 is the MSI version of

the Look-Ahead Carry Generator, which provides identical inputs and outputs except for the C4

output which is available in the form of P and G output pins to allow a second level Cascading.

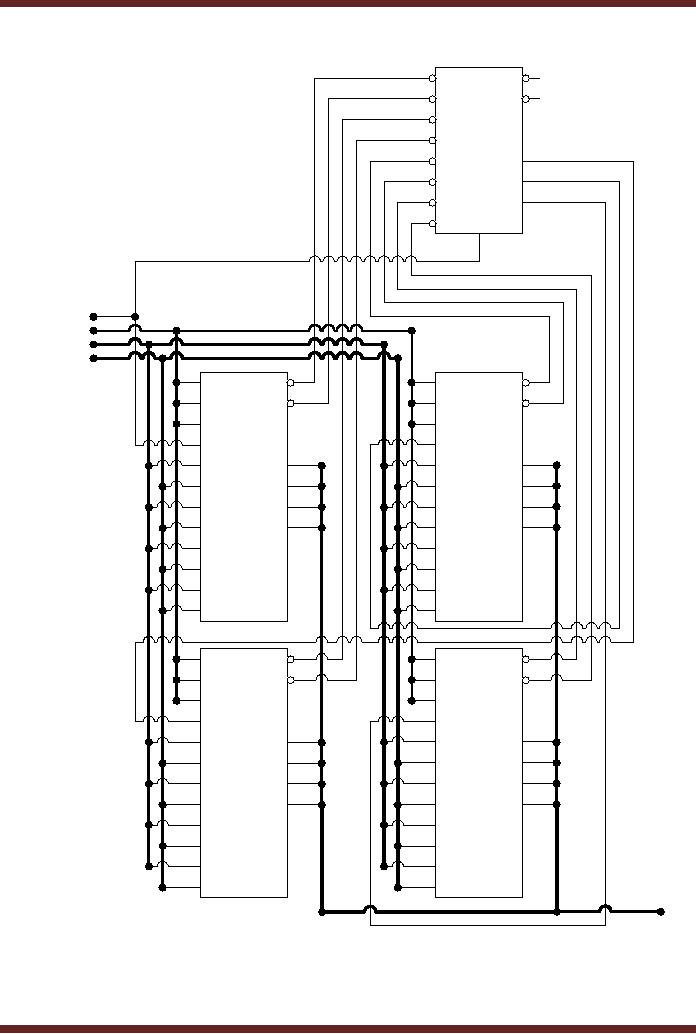
The connection of four 74XX381 4-bit ALUs and a 74XX182 to implement a 16-bit ALU is

shown. Figure 16.3

The inputs A, B and the output F of the four, 4-bit ALUs 0, 1, 2 and 3 are connected to

appropriate bits of the 16-bit inputs A, B and output F respectively. Thus bits A(0-3), B(0-3)

and F(0-3) are connected to inputs and output of ALU0, bits A(4-7), B(4-7) and F(4-7) are

connected to inputs and output of ALU1, bits A(8-11), B(8-11) and F(8-11) are connected to

inputs and output of ALU2 and bits A(12-15), B(12-15) and F(12-15) are connected to inputs

and output of ALU3. The Group-Carry Generate and Propagate outputs of the four ALUs are

connected to the inputs of Look-Ahead Carry generator 74X182 respectively. The Carry

outputs C1, C2 and C3 from the Look-Ahead Carry generator circuit are generated after a gate

delay of 2 and are connected to the Carry in pins of ALUS 1, 2 and 3 respectively.

151

CS302 - Digital Logic & Design

74X182

C12

S(0-2)

A(0-15)

B(0-15)

74X381

Cin

F10

F11

A10

B10

ALU0

ALU2

A11

B11

74X381

Cin

A12

F12

B12

F13

A13

F14

B13

F15

A14

B14

ALU1

ALU3

A15

B15

F(0-15)

Figure 16.3

16-bit ALU

Comparators

152

CS302 - Digital Logic & Design

The basic function of a Comparator is to compare two binary quantities and to

determine if the two quantities are equal. If the quantities are not equal then it has to

determine which of the two quantities is greater than the other. Many Integrated Circuit

Comparators have three outputs to indicate A=B, A>B and A<B.

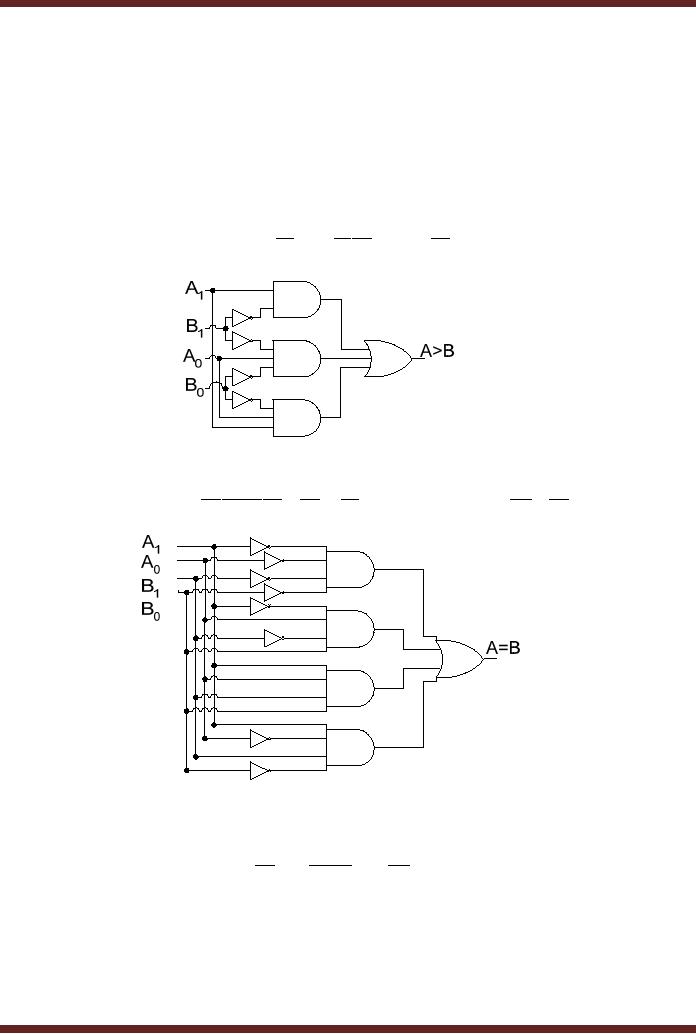
Earlier, simplified Boolean expressions for a 2-bit Comparator circuit were determined

that compares two 2-bit numbers and sets one of its three outputs to indicate A=B, A>B or

A<B. The Booleans expressions representing the three outputs are presented. The three

Combinational Circuits implementing the three outputs are also shown. Figure 16.4

(A > B) = A 1B1 + A 0 B1B 0 + A 1A 0 B 0

Figure 16.4a Implementation of A>B

(A = B) = A 1 A 0 B1B 0 + A 1A 0 B1B 0 + A 1A 0B1B 0 + A 1 A 0B1B 0

Figure 16.4b Implementation of A=B

(A < B) = A 1B1 + A 1 A 0B 0 + A 0B1B 0

153

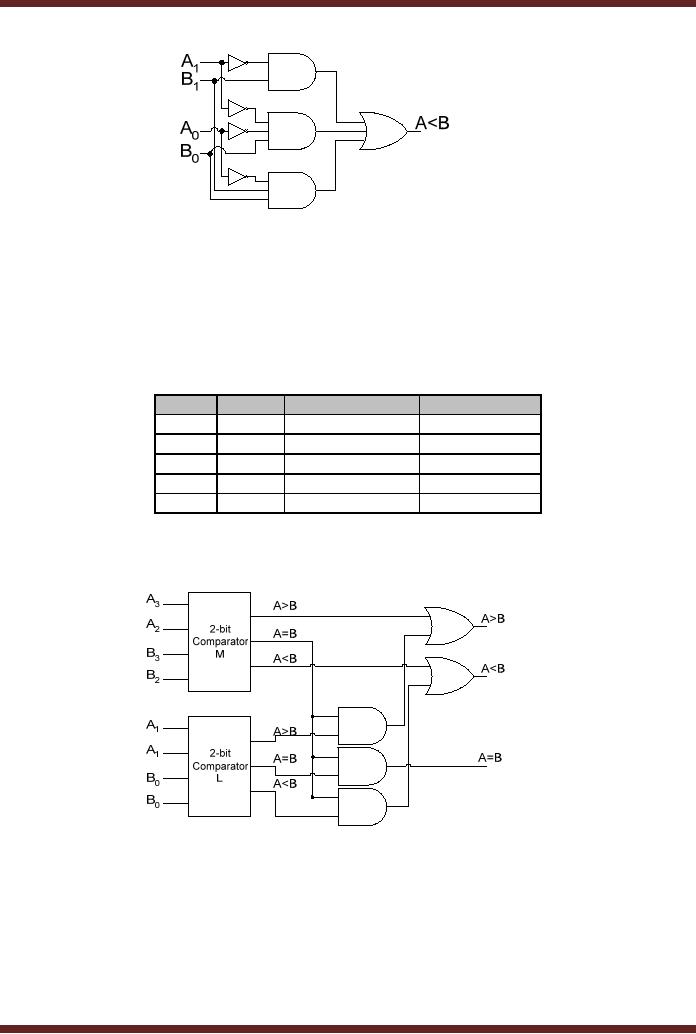
CS302 - Digital Logic & Design

Figure 16.4c Implementation of A<B

The 2-bit Comparator discussed earlier is considered to be a Parallel Comparator as all

the bits are compared simultaneously. External Logic has to be used to Cascade together two

such Comparators to form a 4-bit Comparator.

The 4-bit numbers compared by the Cascaded implementation are represented in table

16.1.

Comparator M

Comparator L

1101

0111

A>B

0110

1011

A<B

0011

0010

A=B

A>B

0100

0101

A=B

A<B

1001

A=B

Table 16.1

Comparison of numbers by Cascaded 4-bit Comparator

Figure 36.5

Implementation of 4-bit Comparator by Cascading two 2-bit Comparators

The two most significant bits of 4-bit numbers A and B are compared by the Most

Significant 2-bit Comparator M and the least significant two bits are compared by the Least

Significant 2-bit Comparator L. Figure 16.5 If the two most significant bits of number A are

greater than the two most significant bits of number B, (A=1101 and B =0111) the Most

Significant Comparator indicates A>B and there is no need to compare the remaining two least

significant bits. Similarly, if the two most significant bits of numbers A and B (A=0110 and

B=1011) are compared by the Most Significant Comparator and the comparator sets its A<B

154

CS302 - Digital Logic & Design

then there is no need to compare the remaining two least significant bits. However, if the two

most significant bits of numbers A and B indicates A=B then least significant two bits have to

be compared to determine if A>B (A=0011 B=0010), A<B (A=0100 B=0101) or A=B (A=1001

B=1001). Thus the A=B output of the Most Significant 2-bit Comparator is used to enable three

AND gates. The output of only one AND gate is set to 1 depending upon the output of the

Least Significant 2-bit Comparator.

An alternate method of implementing Comparators which allows the Comparators to be

easily cascaded without the need for extra logic gates by Iterative Circuit based Comparators.

Iterative Circuit based Comparator

An Iterative circuit is implemented using identical modules each of which has Primary

Inputs and Outputs and Cascading Inputs and Outputs. The Cascading inputs of the least

significant module are connected to fixed logic inputs and the Cascading outputs are

connected to the Cascading inputs of the next significant module. A 2-bit Iterative Circuit

based Comparator is shown. Figure 16.6.

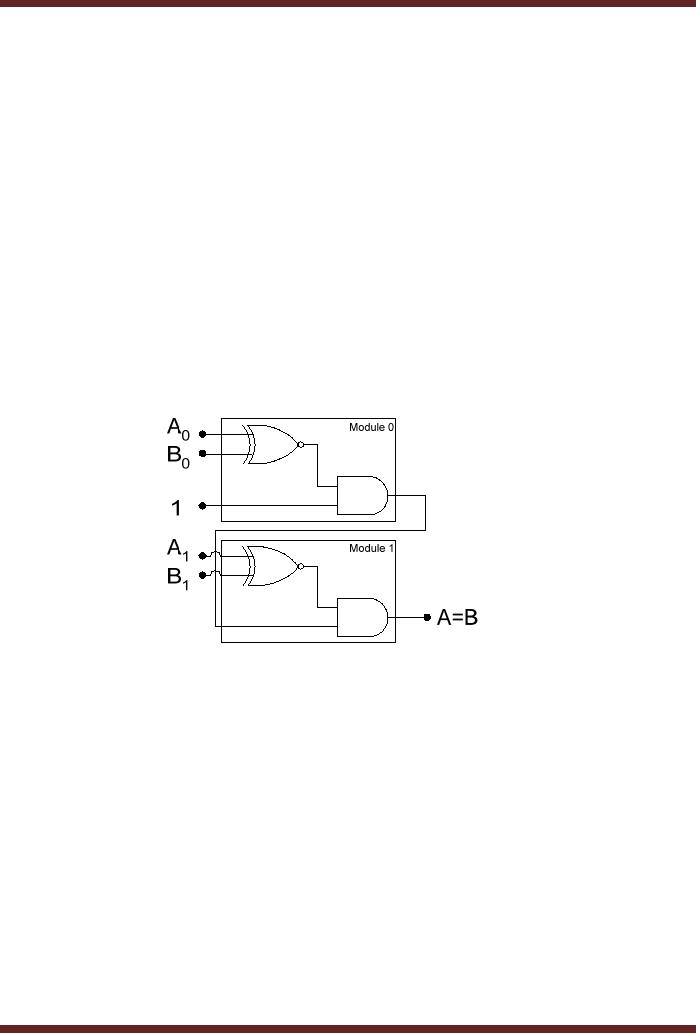
Figure 16.6a Iterative Circuit Implementation of A=B function

The Cascading input of Module 0 is connected to logic 1. If input A0 is equal to input B0,

the XNOR gate output in Module 0 is a 1 which is passed on to Module 1 through its

Cascading input. The output A=B is 1 when input A1 is equal to B1. If either A0 ≠ B0 or A1 ≠ B1

the output A=B is 0. The Equality Comparing circuit can be expanded to 4-bits by Cascading

two Modules connecting their respective Cascading inputs and outputs.

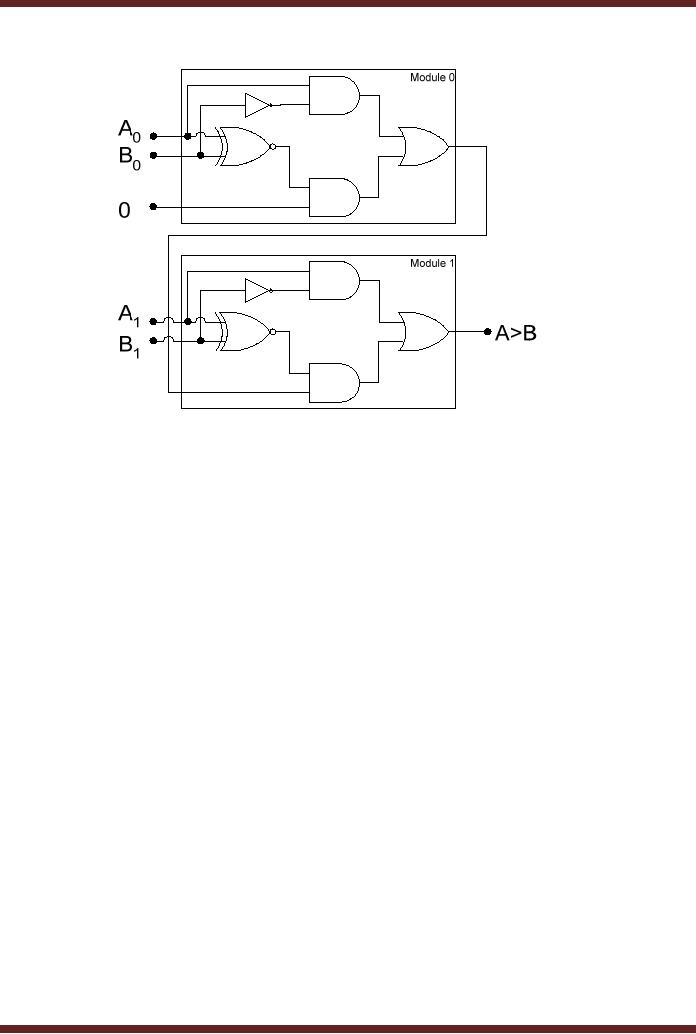
In the Iterative Circuit for A>B, the Cascading input of Module 0 is connected to Logic

0. The output of Module 0 is 1 when A0>B0. The Cascading output of Module 0 is connected to

the Cascading input of Module 1. The output A>B of Module 1 is 1 if A1=B1 and Cascading

input is 1, or if A1>B1.

155

CS302 - Digital Logic & Design

Figure 16.6b Iterative Circuit Implementation of A>B function

Similar Iterative Circuit for A<B, allows multiple modules to be Cascaded together to

form multi-bit A<B unit.

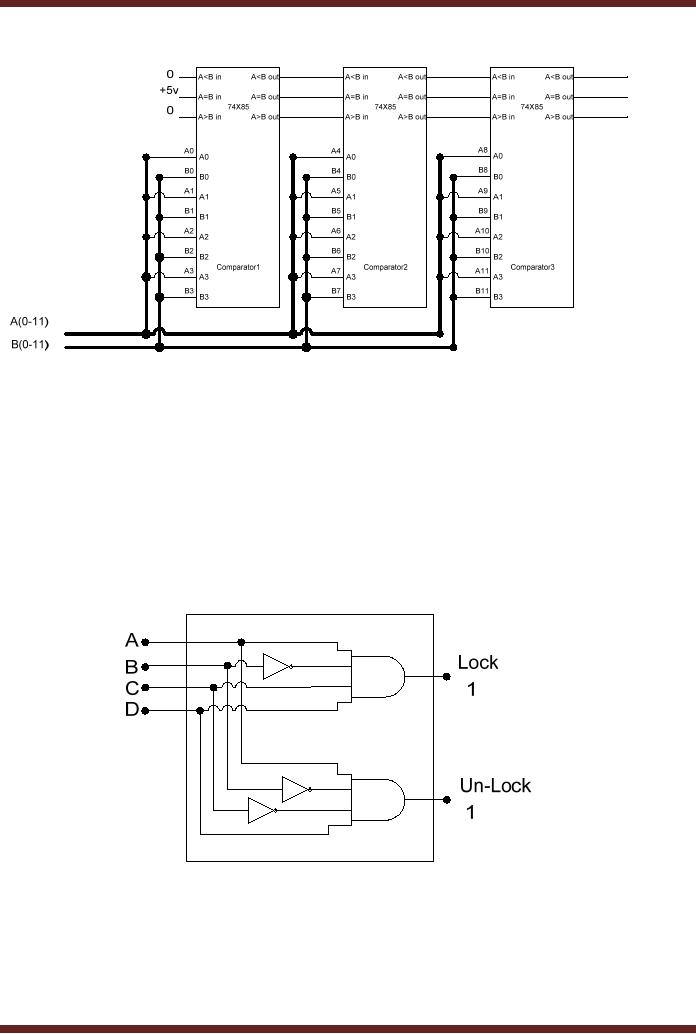
MSI 4-bit Comparator

MSI 74HC85 4-bit Iterative Circuit based Comparator allows multiple 74HC85s to be

cascaded together to form Comparators N x 4-bit Comparators. Three 74HC85s cascaded

together forms a 12-bit Comparator circuit. Figure 16.7.

Three Comparators are cascaded together. Comparator 1 compares the least

significant bits 0 to 3, Comparator 2 compares bits 4 to 7 and Comparator 3 compares the

most significant bits 8 to 11. The respective input bits are shown connected to the three

comparators through thick lines. The Cascading inputs of Comparator 1 are permanently

connected to Ground and +5 volts. A<B in and A>B in are connected to ground and A=B in is

connected to +5 Volts. The cascading outputs of Comparator 1 are connected to the

respective cascading inputs of comparator 2. Similarly, the cascading outputs of Comparator 1

are connected to the cascading inputs of Comparator 3. The final output of the 12-bit

Comparator circuit is available at the cascading outputs of Comparator 3.

156

CS302 - Digital Logic & Design

Figure 16.7

12-bit Comparator

Decoders

A Decoder has multiple inputs and multiple outputs. The Decoder device accepts as an

input a multi-bit code and activates one or more of its outputs to indicate the presence of the

multi-bit code. There are different variations of Decoder devices.

Basic Decoder

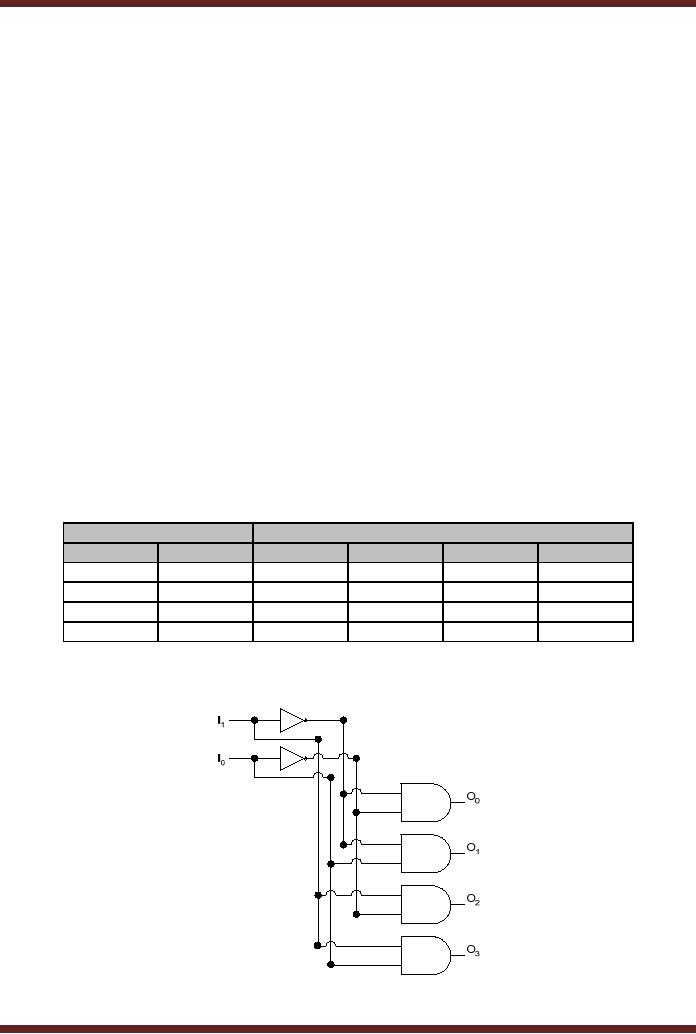
Consider an electronic door lock which unlocks the door when a 4-bit code 1011 is

entered. The door is locked when another 4-bit combination 1001 is entered. The lock and

unlock circuit is implemented using a combination of NOT and AND gates. Figure 16.8

Figure 16.8

Electronic Door Lock

The circuit is configured to activate the Lock output when the Door Lock code 1011 is

applied at inputs ABCD. The Un-Lock output is activated when the Door Un-Lock code 1001 is

applied at the inputs ABCD. The circuit is a Decoder circuit. It detects the Code 1011 and

activates the Lock output. Similarly, it detects the 1001 code and activates the Un-Lock output.

Two different outputs are activated to indicate the presence of two unique 4-bit binary codes.

157

CS302 - Digital Logic & Design

The decoder circuit can be expanded to have more Lock and Un-Lock outputs to Lock and Un-

Lock different doors in a building.

Applications of decoders

Decoders have two major uses in Computer Systems.

1. Selection of Peripheral Devices

Computers have different internal and external devices like the Hard Disk, CD Drive,

Modem, Printer etc. Each of these different devices is selected by specifying different codes. A

decoder similar to the Electronic Door Lock/Unlock circuit is used to uniquely select or

deselect the appropriate devices.

2. Instruction Decoder

Computer programs are based on instructions which are decode by the Computer

Hardware and implemented. The codes 1100010, 1100011, 1110000 and 1000101 represent

Add two numbers, Subtract two numbers, Clear the result and Store the result instructions.

These instruction codes are decoded by an Instruction Decoder to generate signals that

control different logic circuits like the ALU and memory to perform these operations.

Binary Decoder

The simplest and most commonly used Decoders are the n-to-2n Decoders. These

Decoders have n inputs and 2n outputs Each, n-bit input selects 1 out of 2n output code.

A 2-to-4 Decoder is represented by the function table. Table16.2. The 2-to-4 Binary

Decoder circuit is shown. Figure 16.9

Input

Output

Table 16.2

Function Table of a 2-to-4 Binary Decoder

158

CS302 - Digital Logic & Design

Figure 16.9

2-to-4 Decoder

The 2 to 4 Decoder output O0 is activated to Logic 1 when the input is 00. Similarly for

inputs 01, 10 and 11 the outputs O1, O2 and O3 are respectively activated.

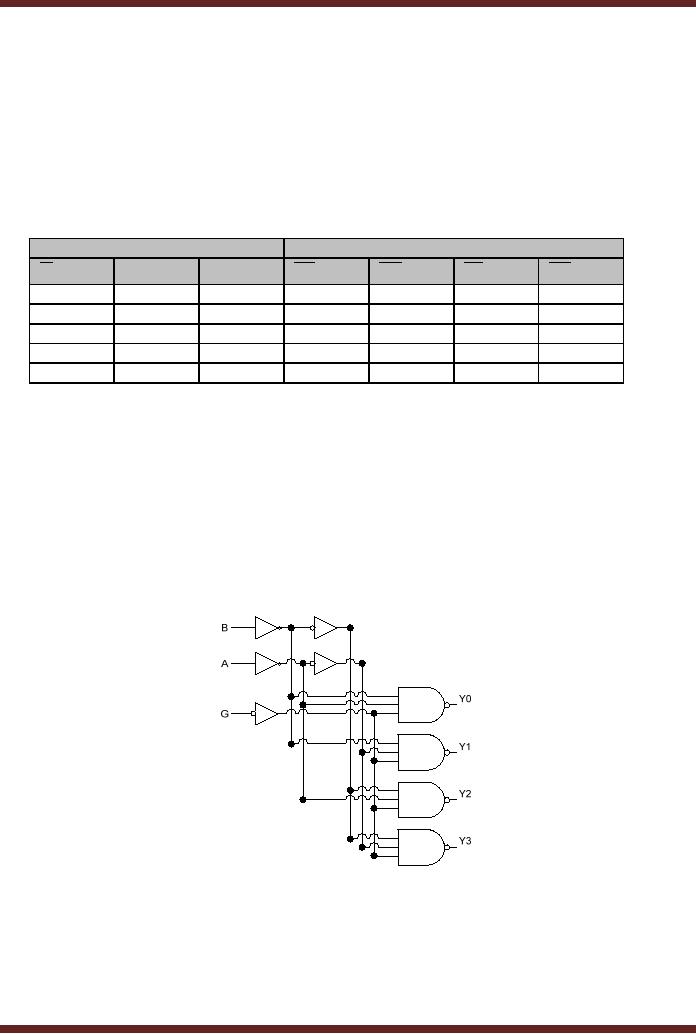
MSI Decoder

The 74LS139 MSI chip has dual 2-to-4 Decoders. The function table, table 16.3, and

the gatelevel circuit diagram for the 2-to-4 Decoder is shown. Figure16.10.The circuit

diagram is slightly different form the one described in figure 16.9.

Input

Output

Table 16.3

Function Table of 74LS139, 2-to-4 Decoder

The 74LS139 has active-low outputs, thus the output which is activated is at logic 0

where as the outputs that ate are not selected are at logic 1. A third active-low input G is the

enable input, which when set to 0 enables all NAND gates. Setting the G input to 1 disables all

NAND gates and all four outputs are at logic 1 the in-active state.

Extra NOT gates are placed at the inputs A and B. Without the two extra NOT gates at

Inputs A and B, each of the two inputs present a unit load of three (a NOT gate and two NAND

gates). By having the extra NOT gates each input presents a single unit load.

Figure 16.10 74LS139, 2-to-4 Decoder

159

Table of Contents: