ODD-PRIME NUMBER DETECTOR, Combinational Circuit Implementation

<< COMPARATOR: Quine-McCluskey Simplification Method

IMPLEMENTATION OF AN ODD-PARITY GENERATOR CIRCUIT >>

CS302 - Digital Logic & Design

Lesson No. 13

ODD-PRIME NUMBER DETECTOR

The table of minterms is represented. Table 13.1

Minterm

Table 13.1

Table of Minterms representing Odd-Prime Numbers

The table of minterms is reorganized in terms of groups of minterms having 0, 1, 2, 3

and 4 1s. Table 13.2

· Minterms 1 has a single 1s

· Minterms 3, 5 and 17 have two 1s each

· Minterms 7, 11, 13 and 19 have three 1s each

· Minterm 23 and 29 have 4 1s

· Minterm 31 has 5 1s

Minterm A

used

Table 13.2

Reorganized Minterms representing Odd-Prime Numbers

In the first step of Quine-McCluskey method minterms are compared to eliminate single

variables. Minterm 1 is compared with minterms 3, 5 and 17 in the next group. Similarly, each

of the 3 minterms 3, 5 and 17 are compared with each of the minterms in the next group

having 3 1s, that is, minterms 7, 11, 13 and 19. Minterms 7, 11, 13 and 19 are compared with

each of the minterms in the next group having 4 1s, that is, minterms 23 and 29. Finally, each

of the two minterms 23 and 29 are compared with the minterm 31 in the last group having all

1s or 5 1s.

118

CS302 - Digital Logic & Design

The results of the comparisons between minterms are represented in a separate table.

Table13.3. The first column lists the minterms that have been compared together to eliminate

common variables. Terms 1 and 3 form a single term eliminating variable D, forming the

product term ABCE . The comparison terms 1 and 3 are marked as used in table 13.2.

Similarly, terms 1 and 5 from a single term eliminating variable C, forming the product

term ABDE . Both these terms are marked as used in table 13.2. Similarly, terms 1, 17

eliminate variable A, terms 3, 7 eliminate variable C, terms 3, 11 eliminate variable B and so

on.

Minterms

Variable used

removed

1,3

1,5

1,17

3,7

3,11

3,19

5,7

5,13

17,19

7,23

13,29

19, 23

23,31

29,31

Table 13.3

Table of minterms, Single variable eliminated

As a result of comparison a total of 14, four variable product terms are formed,

eliminating a single variable from each term. All the 14 terms are represented in table 13.3.

The exhaustive search for finding Prime Implicants has not completed. The results of the

comparisons between two terms in table 13.3 are represented in a separate table. Table 13.4.

Minterms

Variable used

removed

1,3,5,7

2,4

1,3,17,19

2,16

3,7,19,23

4,16

Table 13.4

Table of minterms, Two variable eliminated

The first column lists the terms that have been compared together to eliminate

common variables. So terms, 1, 3, 5 and 7 form a single term eliminating variables C and D,

forming the product term ABE . The comparison terms 1,3 and 5,7 are marked as used in table

13.3. Similarly terms, 1, 3, 17 and 19 from a single term eliminating variable A and D, forming

the product term BCE . Both these terms are marked as used in table 13.3. All the product

terms in table 13.3 are compared to eliminate common variables. No more comparisons of

terms and elimination of variables take place, thus the Prime Implicants have been found.

119

CS302 - Digital Logic & Design

There are 3 Prime Implicants in table 13.4 and 5 Prime Implicant in table 13.3. The

eight Prime Implicants are represented by product terms ACDE , ACDE , BCDE , ACDE ,

ABCE , ABE , BCE and BDE .

In the second step of Quine-McCluskey method the essential and minimal Prime

Implicants are found. The Prime Implicants found in the first step are listed in left most column

of the table. 13.5. All the original minterms are listed in the top row. In each cell an x is marked

indicating that the Prime Implicant listed in the left column covers the minterm mentioned in

the top row. Thus the Prime Implicant ACDE covers the minterms 3 and 11. In other words

minterms 3 and 11 all have the product terms ACDE . The table 13.5 can be directly

implemented from table 13.3 and 13.4.

ACDE

BCDE

ACDE

ABCE

ABE

BCE

BDE

Table 13.5

Table of Prime Implicants

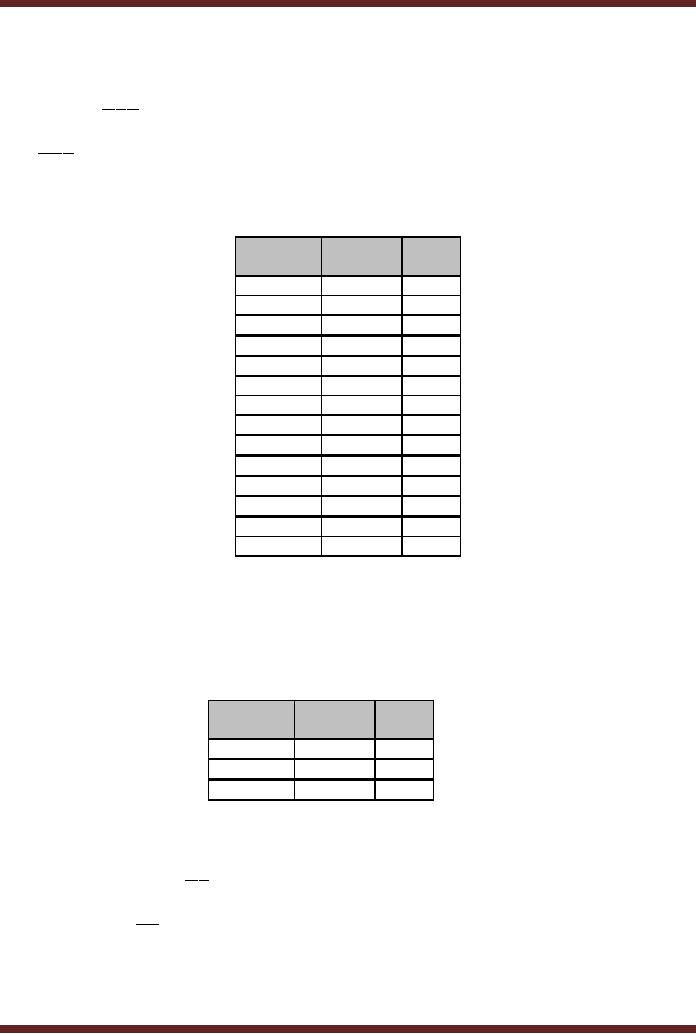
Circles are marked in cells having x, which represent minterms covered by only a

single prime impicant. Thus the minterms 11 and 17 are covered by only the Prime Implicants

ACDE and BCE respectively. These implicants do not cover all the minterms. The other

essential implicants that have minimum number of variables and which cover all the remaining

BCDE , ACDE and ABE . The simplified expression is

minterms are

ACDE + BCDE + ACDE + ABE + BCE . The function can also be represented by the

expression ACDE + ACDE + ABCE + BCE + BDE . In both cases the number of product terms

is the same with same number of variables.

Combinational Logic

Individual gates AND, OR and NOT, NAND and NOR Universal Gates and XOR and

XNOR gates perform unique functions. These gates in their individual capacity can not

perform any useful function. The Logic Gates have to be connected together in different

combinations to form Logic Circuits that are able to perform some useful operation like

addition , comparison etc. These combinations of gates which results in a circuit used to

perform some function are known as Combinational Logic.

The function of any Digital Logic circuit is represented by Boolean expressions. In the

examples discussed earlier, Boolean expressions for various functions have been determined.

Two forms of representing functions through Boolean expressions are the SOP and POS

120

CS302 - Digital Logic & Design

expressions. These two types of Boolean expressions are implemented using a combination of

gates to form Combinational Logic Circuits.

Combinational Circuit Implementation based on SOP form

A standard way to express a Boolean expression is the SOP form. The expression has

several product terms which are summed together through a single OR gate. The product

terms can have variables and their complemented form. A SOP expression is implemented by

using a combinational circuit made up of many AND gates and a single OR gate (AND-OR

gate combination). The inputs to the AND gates can be in the complemented form or the un-

complemented form, requiring the use of NOT gates.

OR Gate

level

AND

Gate

NOT

level

Gate

level

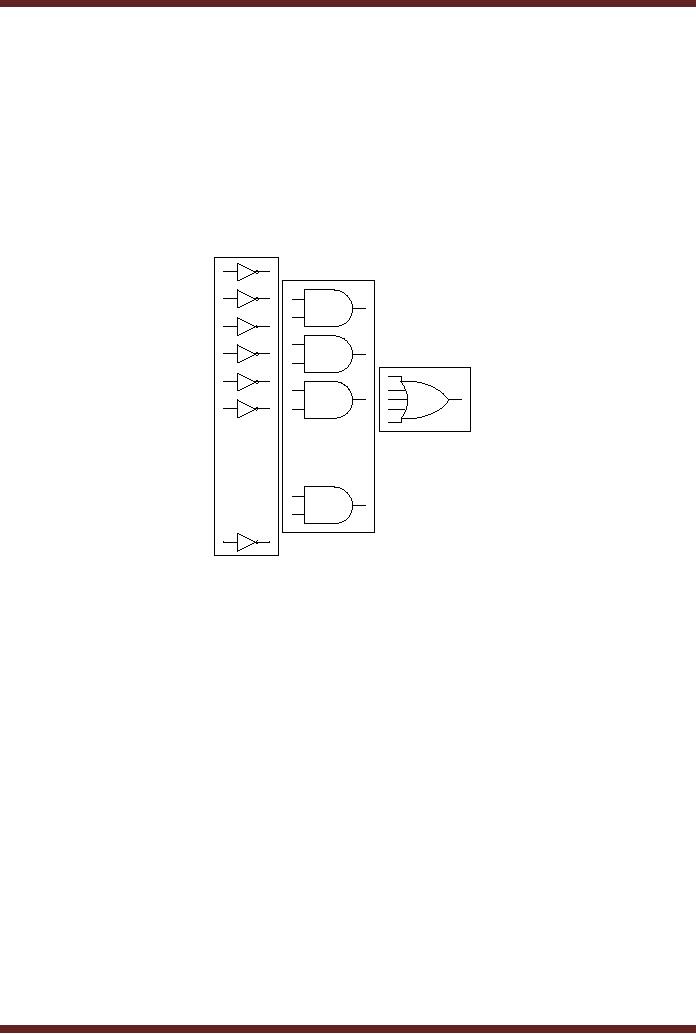
Figure 13.1

General, Combination al Logic Circuit based on SOP form

The diagram shows the general architecture of the SOP Implementation. The

implementation is based on three levels of gates. SOP expression is implemented by the

AND-OR combination of gates. The AND gates produce the product terms. Outputs of all the

AND gates are connected to a single multiple input OR gate for sum of products. The product

terms comprise of literals in their complemented form and un-complemented form which are

implemented by NOT gates connected to the inputs of the AND gates.

Combinational Circuit Implementation based on POS form

A standard way to express a Boolean expression is the POS form. The expression has

several sum terms which are multiplied together through a single AND gate. The sum terms

can have variables and their complemented form. A POS expression is implemented by using

a combinational circuit made up of many OR gates and a single AND gate (OR-AND gate

combination). The inputs to the OR gates can be in the complemented form or the un-

complemented form, requiring the use of NOT gates.

121

CS302 - Digital Logic & Design

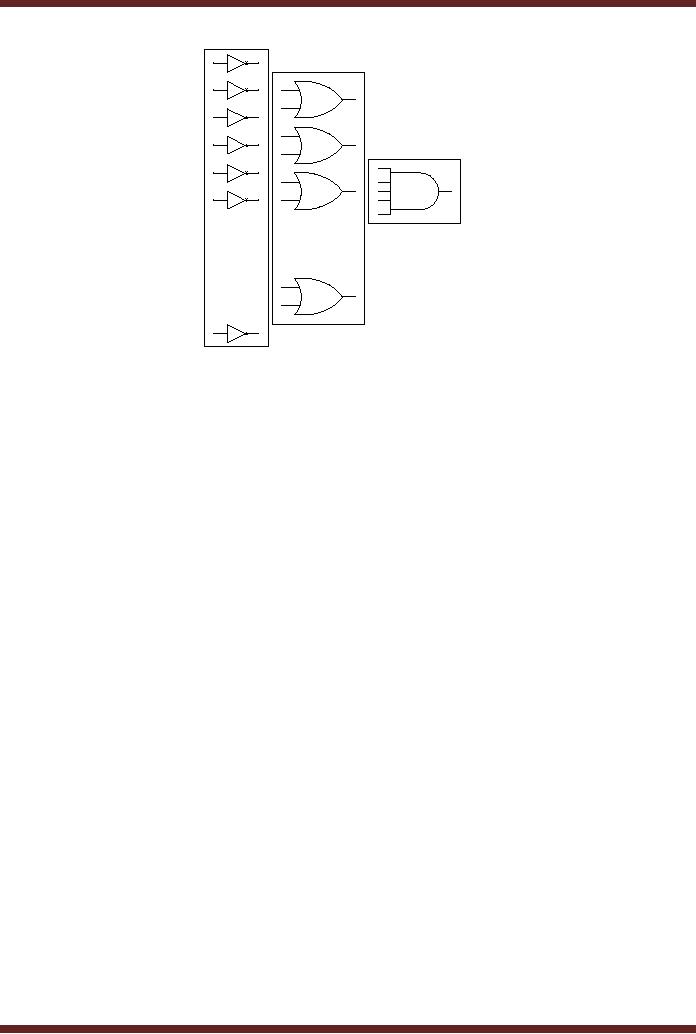
AND

Gate

level

OR Gate

level

NOT

Gate

level

Figure 13.2

General, Combination al Logic Circuit based on POS form

The diagram shows the general architecture of the POS Implementation. The

implementation is based on three levels of gates. POS expression is implemented by the OR-

AND combination of gates. The OR gates produce the sum terms. Outputs of all the OR gates

are connected to a single multiple input AND gate for product of sum terms. The sum terms

comprise of literals in their complemented form and un-complemented form which are

implemented by NOT gates connected to the inputs of the OR gates.

Design and Implementation of Combinational Circuits

The design and implementation of a combinational circuit starts by defining the function

of the Combinational circuit. The function of a combinational circuit is defined by a truth table

or a function table. Once the function table is defined the combinational circuit can be directly

implemented from the function table.

Direct implementation of a combinational circuit from the function table results in a

circuit which uses maximum number of gates organized at three levels. This increases the

cost, the size of the circuit and the power requirement of the Combinational circuit. The

propagation delay of the circuit is of the order of three gates. Therefore, before implementing

the circuit the expression is simplified using the manual method by applying rules, laws and

theorems of Boolean Algebra or by the Karnaugh map method or the Quine-McCluskey

method if the number of variables exceeds 4.

Implementation of an Adjacent 1s Detector Circuit

A circuit that checks an input number and determines if it has two adjacent 1s is

considered to explain the entire process of design and implementation of a typical

Combinational Logic Circuit. The Adjacent 1s detector circuit is implemented using the

standard SOP and POS forms of Boolean expressions. The circuit is also implemented using

the simplified Boolean expressions. The alternate form of implementing the circuit using only

NAND or NOR gates is also discussed.

122

CS302 - Digital Logic & Design

1. SOP based Implementation of the Adjacent 1s Detector Circuit

The Adjacent 1s Detector accepts 4-bit inputs. If two adjacent 1s are detected in the

input, the output is set to high. The operation of the Adjacent 1s Detector is represented by the

function table. Table 13.6. In the function table, for the input combinations 0011, 0110, 0111,

1011, 1100, 1101, 1110 and 1111 the output function is a 1.

Input

Output

Input

Output

Table 13.6

Function Table of Adjacent 1s Detector

Implementing the circuit directly from the function table based on the SOP form

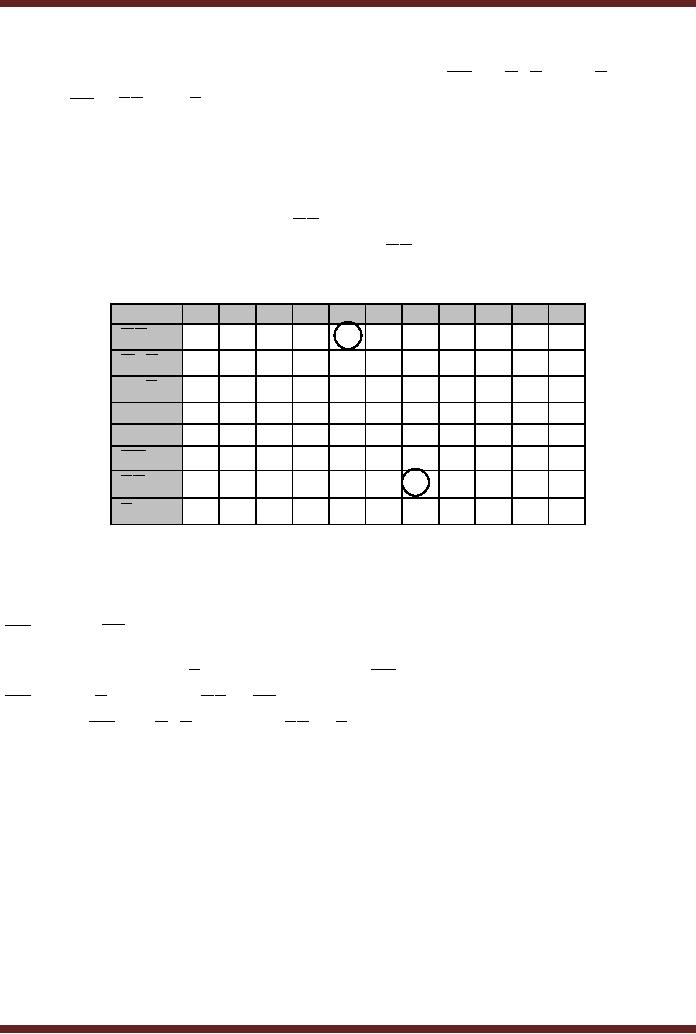
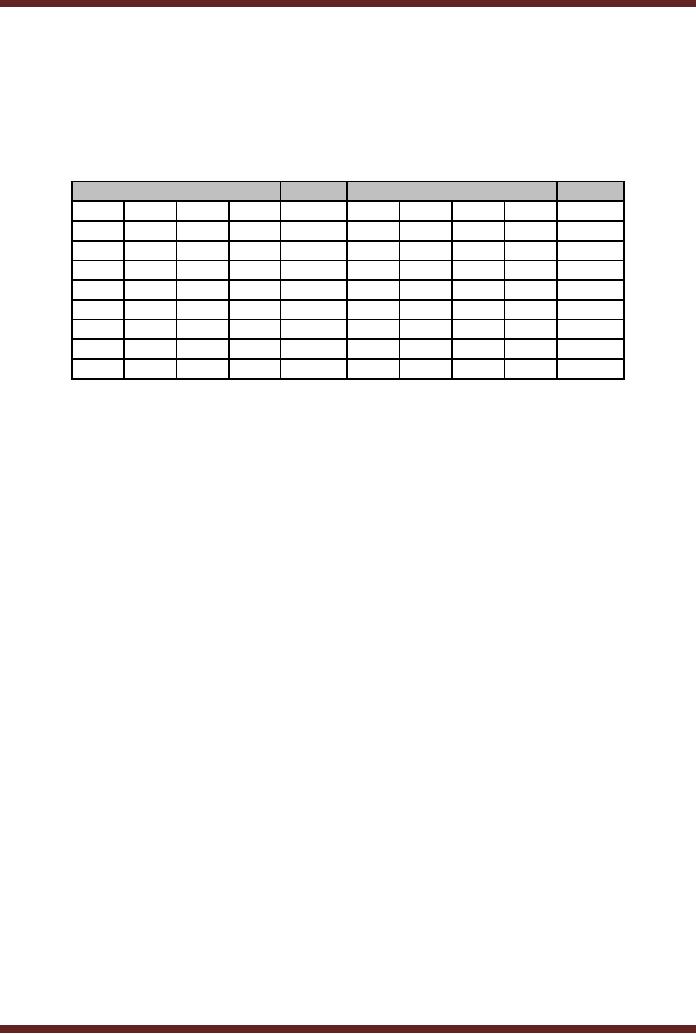
requires 8 AND gates for the 8 product terms (minterms) with an 8-input OR gate. Figure 13.3.

The total gate count is

· One 8 input OR gate

· Eight 4 input AND gates

· Ten NOT gates

The expression can be simplified using a Karnaugh map, figure 13.4, and then the

simplified expression can be implemented to reduce the gate count. The simplified expression

is AB + CD + BC . The circuit implemented using the expression AB + CD + BC has reduced

to 3 input OR gate and 2 input AND gates. Figure 13.5

123

CS302 - Digital Logic & Design

Figure 13.3

SOP Implementation of Adjacent 1s Detector

AB\CD

Figure 13.4

Simplification of Adjacent 1s Detector SOP Boolean Expression

Figure 13.5

Simplified SOP based Adjacent 1s Detector

The simplified Adjacent 1s Detector circuit uses only four gates reducing the cost, the

size of the circuit and the power requirement. The propagation delay of the circuit is of the

order of two gates.

The simplified Adjacent 1s Detector circuit can be implemented using only NAND

Gates. The AND-OR combinational circuit can be easily replaced by a NAND based

implementation without changing the number of gates. Figure 13.6.

124

CS302 - Digital Logic & Design

Figure 13.6

NAND based Adjacent 1s Detector

Bubbles representing NOT gates are placed at the output of the three AND gates.

Converting the three AND gates to NAND gates. To balance out the three NOT gates added at

the outputs of the three AND gates, three bubbles representing three NOT gates are also

placed at the three inputs of the OR gate. The Resulting OR gate symbol with three bubbles at

the three inputs is an alternate symbol for a three input NAND gate.

Implementing Combinational Logic Circuits using only NAND gates helps in reducing

the circuit size and cost as the Integrated Circuit packages multiple gates in a single package.

If, for example, the 3-input NAND gate in the circuit had been a 2-input NAND gate, only a

single IC package (74LS00) would have been required. For the circuit shown in figure 13.5 two

separate IC packages (74LS08 and 74LS32) are required.

2. POS based Implementation of the Adjacent 1s Detector Circuit

A combinational Adjacent 1s Detector circuit can be implemented, based on the POS

form. It was discussed earlier that it is very easy to switch between SOP and the POS

representations using the information in a function table or the information mapped to a

Karnaugh Map. Referring to the Function Table for the Adjacent 1s Detector. Table 13.6 a

POS based Adjacent 1s Detector circuit can be easily implemented by using the Sum terms

(Maxterms). The POS based circuit for this particular case has 8 sum terms which require 8

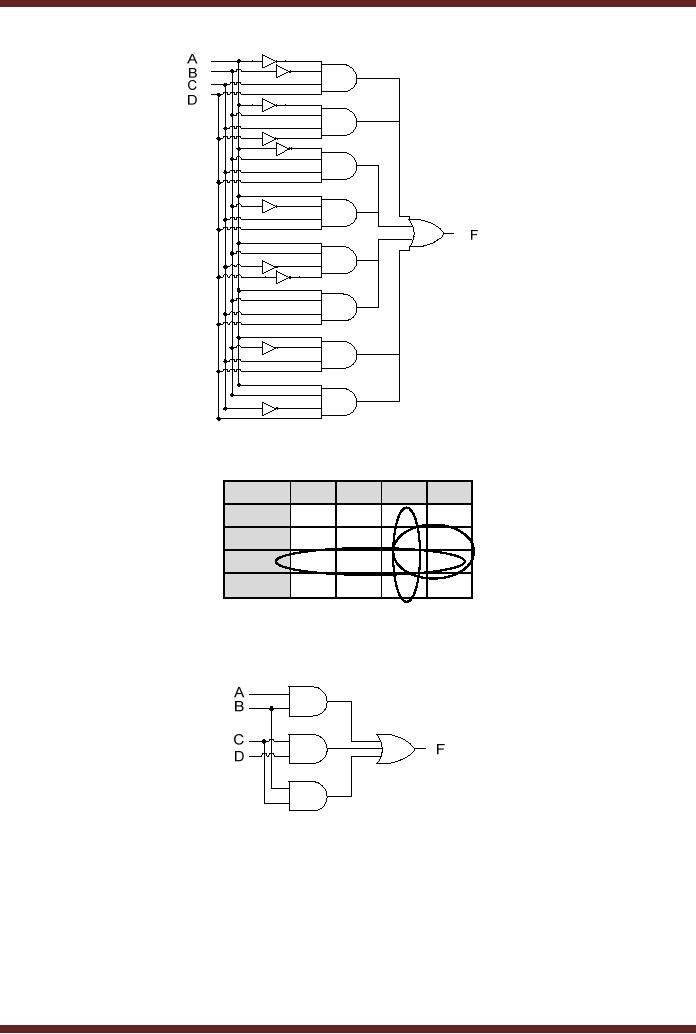
OR gates and a single 8-input AND gate. Figure 13.7. The total gate count is

· One 8 input AND gate

· Eight 4 input OR gates

· Ten NOT gates

Both, the SOP based circuit discussed earlier and the POS based circuit give identical

outputs for identical set of input combinations. One practical purpose of using either the SOP

or the POS based implementation is to reduce the size of the circuit and have a simpler circuit.

In the example of Adjacent 1s Detector circuit both the SOP and POS based implementations

have equal number of minterms (8) and maxterms (8) thus both implementation use exactly

the same number of gates (19). In many cases, the function describing the operation of a

combinational circuit has minterms which are either less than or more than the number of

maxterms. Thus it is wiser to choose the implementation form that uses the least number of

minterms or maxterms to achieve a combinational circuit that uses the least number of gates.

125

CS302 - Digital Logic & Design

Figure 13.7

POS Implementation of Adjacent 1s Detector

The POS expression can be simplified using a Karnaugh map. Figure 13.8, the simplified

expression can be implemented to reduce the gate count. The simplified expression is

(A + C)(B + C)(B + D)

AB\CD

Figure 13.8

Simplification of Adjacent 1s Detector POS Boolean Expression

Figure 13.9

Simplified POS based Adjacent 1s Detector

126

CS302 - Digital Logic & Design

The simplified Adjacent 1s Detector circuit uses only four gates reducing the cost, the

size of the circuit and the power requirement. The propagation delay of the circuit is of the

order of two gates.

The simplified Adjacent 1s Detector circuit can be implemented using only NOR Gates.

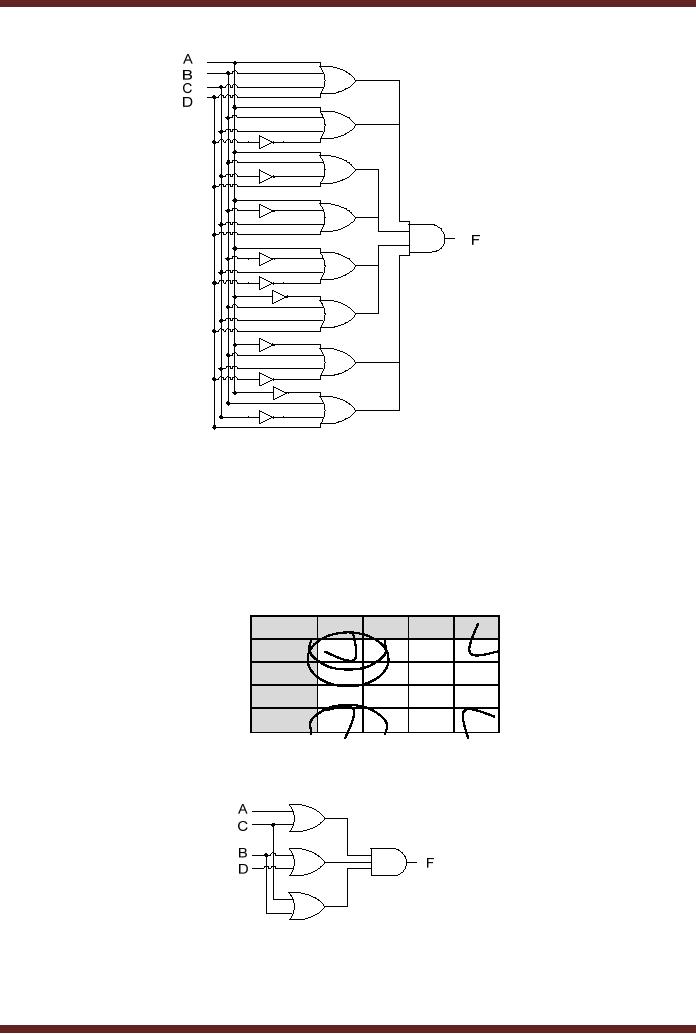
The OR-AND combinational circuit can be easily replaced by a NOR based implementation

without changing the number of gates. Figure 13.10.

Figure 13.10

NOR based Adjacent 1s Detector

Bubbles representing NOT gates are placed at the output of the three OR gates,

converting the three OR gates to NOR gates. To balance out the three NOT gates added at

the outputs of the three OR gates, three bubbles representing three NOT gates are also

placed at the three inputs of the AND gate. The Resulting AND gate symbol with three bubbles

at the three inputs is an alternate symbol for a three input NOR gate.

Operation of Adjacent 1s detector Circuit

The operation of a Combinational Logic Circuit can be verified by applying varying set

of signals at the input of the circuit and comparing the output of the combinational circuit with

the corresponding outputs in the Function Table. If the varying set of inputs and the

corresponding outputs are plotted over a period of time, the timing diagram thus obtained,

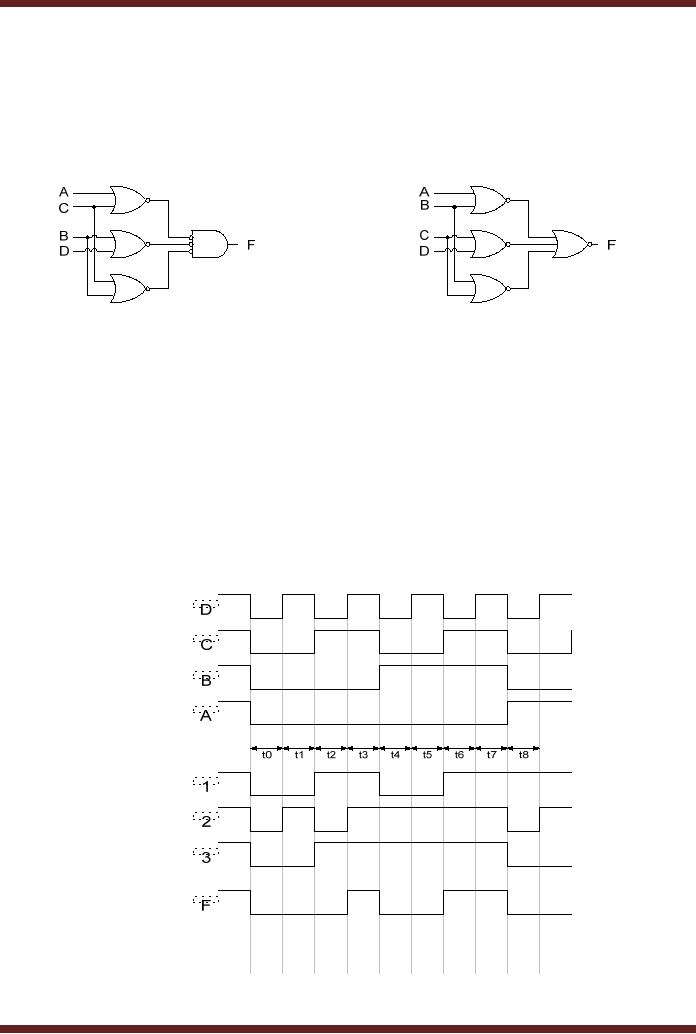
describes the operation of the circuit. Figure 13.11

Figure 13.11 Timing Diagram of the Adjacent 1s Detector

127

CS302 - Digital Logic & Design

To prove that the SOP and POS based Adjacent 1s Detector combinational circuits

synthesized from the Function table. Table 13.6 are identical, the timing diagram, figure 13.11

is based on the operation of the POS based simplified circuit. Figure 13.9

The timing diagram is for time intervals t0 to t8. A, B, C and D are the inputs to the

circuit which are shown changing with time. The timing signals 1, 2 and 3 represent the

outputs of the OR gates 1, 2 and 3. The timing signal F represents the output of the circuit.

At interval t0 the input ABCD to the circuit is 0000, the outputs of the three OR gates is

0, 0 and 0 and the circuit output is also 0. At the interval t3 the input ABCD to the circuit is

0011, the outputs of OR gates 1, 2 and 3 are 111. The output F is also a 1, which indicates

adjacent 1s. At interval t6 the input ABCD to the circuit is 0110, the outputs of OR gates 1, 2

and 3 are 111. The output F is again 1 indicating adjacent 1s.

The operation of the circuit which is based on the POS simplified expression also

proves that a POS based expression determined from the truth table and K-map results in a

circuit which operates in an identical manner to that of a SOP based circuit.

Active low/high Inputs and Outputs

The circuits discussed so far have their output set to when to indicate an active state.

For example, the output of the BCD to 7-Segment Decoder circuit has its seven segment

outputs set to 1 to indicate a segment that has been selected. Similarly, the Comparator

circuit's three outputs are normally at binary 0. The appropriate output is set to 1 to indicate

the relationship between the two numbers. The Odd-Prime Number detector circuit output

normally is set at 0. It is activated to 1 to indicate an Odd-Prime number. The Adjacent 1s

Detector circuit also sets its output to active 1 to indicate detection of Adjacent 1s. All the four

circuits have an active-high output. That is, normally the output is at logic 0. The output is set

to 1 to indicate an active state.

Combinational circuits can have an active-high output or an active-low output. An

active-high or active-low output doesn't effect the operation of the combinational circuit in any

manner. To convert a circuit having an active-high output to active low-output requires the

inversion of the circuit output by connecting a NOT gate. Symbolically, a bubble is added to

the circuit output. Thus, circuits having a bubble at their outputs are considered to have an

active-low output.

Circuits can also have active-high or active-low inputs. The operation of the circuits

having an active-high input is not any different from that of an active-low input circuit. Active-

low input circuits are activated on a logic 0 input. Circuits having an active-low input have

bubbles connected to circuits inputs. The four circuits discussed so far have active-high inputs.

The four logic gates AND, OR, NAND and NOR can be described in terms of their input

and output logic levels. The AND gate doesn't have any bubbles at its inputs or output. The

AND gate performs AND operation on two active high inputs to result in an active high output.

The OR gate also doesn't have any bubbles at its inputs and output. OR gate performs OR

operation on two active high inputs to result in an active high output. The NAND and NOR

gates have a bubble at their outputs. Their operation can be described in terms of AND and

OR gates. NAND gate performs AND operation on two active high inputs resulting in an active

low output. The NOR gate performs OR operation on two active high inputs to result in an

active low output

128

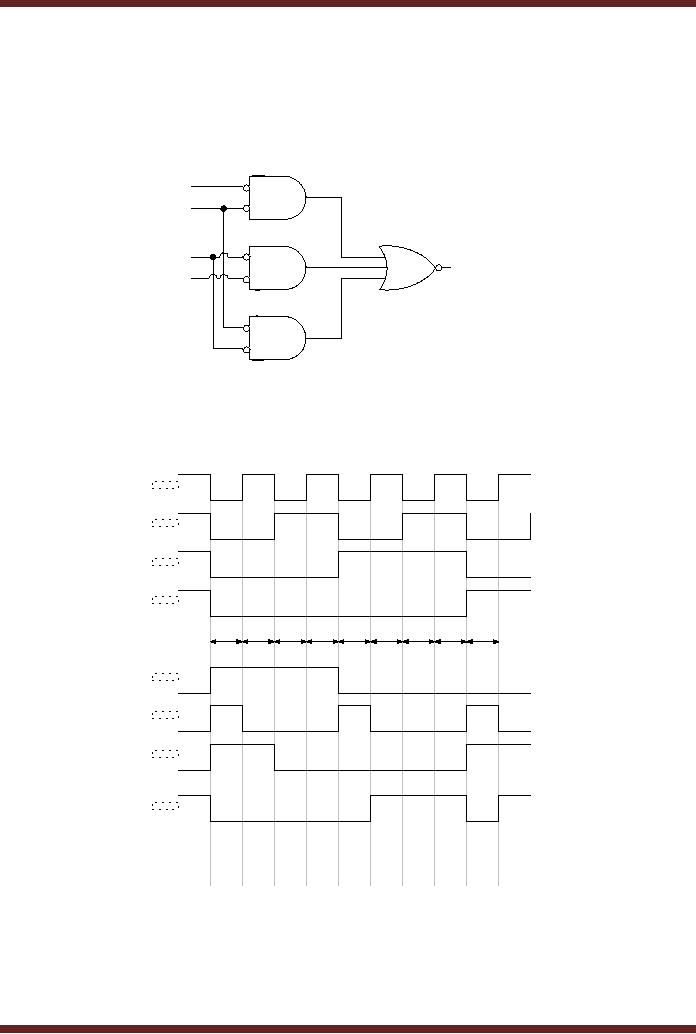
CS302 - Digital Logic & Design

To help understand active-low input, consider the active-high input and active-high

output SOP circuit. Fig. 13.5 which is converted into an active-low input and output circuit by

connecting NOT gates at the circuit inputs and outputs. Figure 13.12. The circuit operation is

verified with the help of a timing diagram. Figure 13.13.

Figure 13.12

SOP based active-low input and output Adjacent 1s Detector

Figure 13.13 Timing Diagram of the active-low input/output Adjacent 1s Detector

The timing diagram describes the operation of the circuit for the intervals t0 to t8. The

timing signals A, B, C and D represent the active-low inputs applied at the inputs. The timing

signals 1, 2 and 3 represent the outputs of the NOR gates 1, 2 and 3 respectively, shown in

their alternate symbolic form. The timing signal F represents the active-low output.

129

CS302 - Digital Logic & Design

At interval t0 the active-low input at inputs ABCD is 0000 which actually represents

1111. The active-low output F is 0 which indicates that adjacent 1s have been detected.

Similarly at intervals t1 to t4, the active-low inputs ABCD 0001, 0010, 0011 and 0100 actually

represent the numbers 1110, 1101, 1100 and 1011, the output is 0 indicating that adjacent 1s

have been detected.

Implementation of an Odd-Parity Generator Circuit

Consider the second example of a circuit to generate odd parity. The circuit checks an

8-bit number and generates a parity bit to fulfil the Odd-Parity condition. The 8-bit data and the

parity bit are communicated to the receiver circuit. The receiver circuit checks the 8-bit data

and the parity bit to determine if an error has occurred.

The first step in implementing any circuit is to represent its operation in terms of a Truth

or Function table. The function table for an 8-bit data as input has 28 has 256 input

combinations, which becomes unmanageable. Therefore, for the sake of simplicity a 4-bit data

with odd parity is assumed. The receiver circuit is also based on the 4-bit data.

130

Table of Contents: