 |
Microeconomics
ECO402
VU
Lesson
19
A
Firm's Short-Run Costs
($)
Rate
Fixed
Variable
Total
Marginal
Average
Average
Average
of
cost
cost
cost
cost
fixed
variable
total
output
FC
VC
TC
MC
cost
cost
cost
AFC
AVC
ATC
0
50
0
50
1
50
50
100
50
50
50
100
2
50
78
128
28
25
39
64
3
50
98
148
20
16.5
32.7
49.3
4
50
112
162
14
12.5
28
40.5
5
50
130
180
18
10
26
36
6
50
150
200
20
8.3
25
33.3
7
50
175
225
25
7.1
25
32.1
8
50
204
254
29
6.3
25.5
31.8
9
50
242
292
38
5.6
26.9
32.4
10
50
300
350
58
5
30
35
11
50
385
435
85
4.5
35
39.5
Consequently
(from the table):
MC decreases
initially with increasing
returns
�
0 through 4
units of output
MC increases
with decreasing
returns
�
5 through 11
units of output
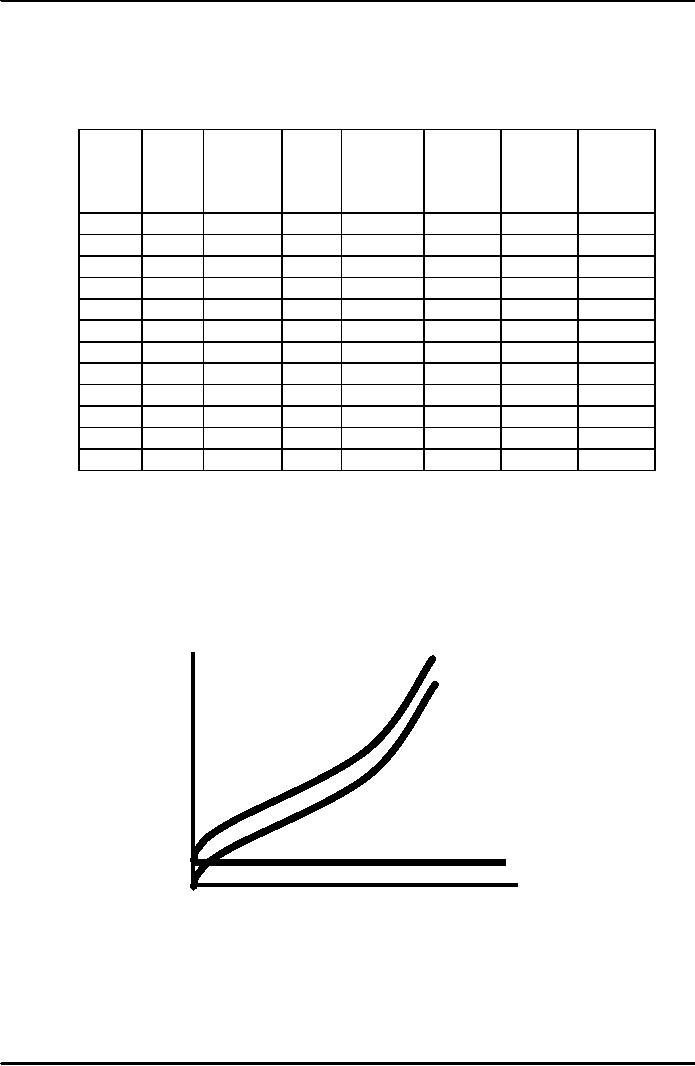
Total
cost
TC
is
the vertical
Cost
sum
of FC
($
per 400
and
VC.
VC
year)
Variable
cost
increases
with
300
production
and
the
rate varies with
increasing
&
decreasing
returns.
200
Fixed
cost does not
100
vary
with output
FC
50
Output
0
1
2
3
4
5
6
7
8
9
10
11
12
13
95

Microeconomics
ECO402
VU
Cost
100
($
per
unit)
MC
75
50
ATC
AVC
25
AFC
1
0
2
3
4
5
6
7
8
9
10
11
Output
(units/yr.)
The
line drawn from the
origin to the tangent of the
variable cost curve:
Its
slope equals AVC
The
slope of a point on VC equals
MC
Therefore,
MC = AVC at 7 units of output (point
A)
Unit
Costs
AFC
falls continuously
When
MC < AVC or MC < ATC, AVC & ATC
decrease
When
MC > AVC or MC > ATC, AVC & ATC
increase
MC
= AVC and ATC at minimum AVC and
ATC
Minimum
AVC occurs at a lower output
than minimum ATC due to
FC
The
User Cost of Capital
User
Cost of Capital = Economic
Depreciation + (Interest Rate)(Value of
Capital)
Example
�
An Airline
buys a Boeing 737 for
$150 million with an
expected life of 30
years
Annual economic
depreciation = $150 million/30 = $5
million
Interest rate
= 10%
�
User
Cost of Capital = $5 million +
(.10) ($150 million
depreciation)
Year 1 = $5
million + (.10)($150 million) =
$20 million
Year 10 = $5
million + (.10) ($100
million) = $15
million
Rate per
dollar of capital
�
r = Depreciation
Rate + Interest Rate
Airline
Example
�
Depreciation
Rate = 1/30 = 3.33/yr
�
Rate of
Return = 10%/yr
User Cost of
Capital
�
r = 3.33 + 10 =
13.33%/yr
96
Microeconomics
ECO402
VU
The
Cost Minimizing Input
Choice
Assumptions
�
Two
Inputs: Labor (L) &
capital (K)
�
Price of
labor: wage rate
(w)
�
The price
of capital
R = depreciation
rate + interest rate
Question
�
If capital
was rented, would it change
the value of r ?
The
Isocost Line
C
= wL + rK
Isocost: A line
showing all combinations of L & K
that can be purchased for
the same
cost
Rewriting
C
as
linear:
�
K = C/r -
(w/r)L
�
Slope of
the Isocost:
()
ΔK
=-
w
ΔL
r
is
the ratio of the wage
rate to rental cost of
capital.
This
shows the rate at which
capital can be substituted
for labor with no
change
in cost.
Choosing
Inputs
�
We
will address how to minimize
cost for a given level of
output.
�
We
will do so by combining Isocosts
with Isoquants
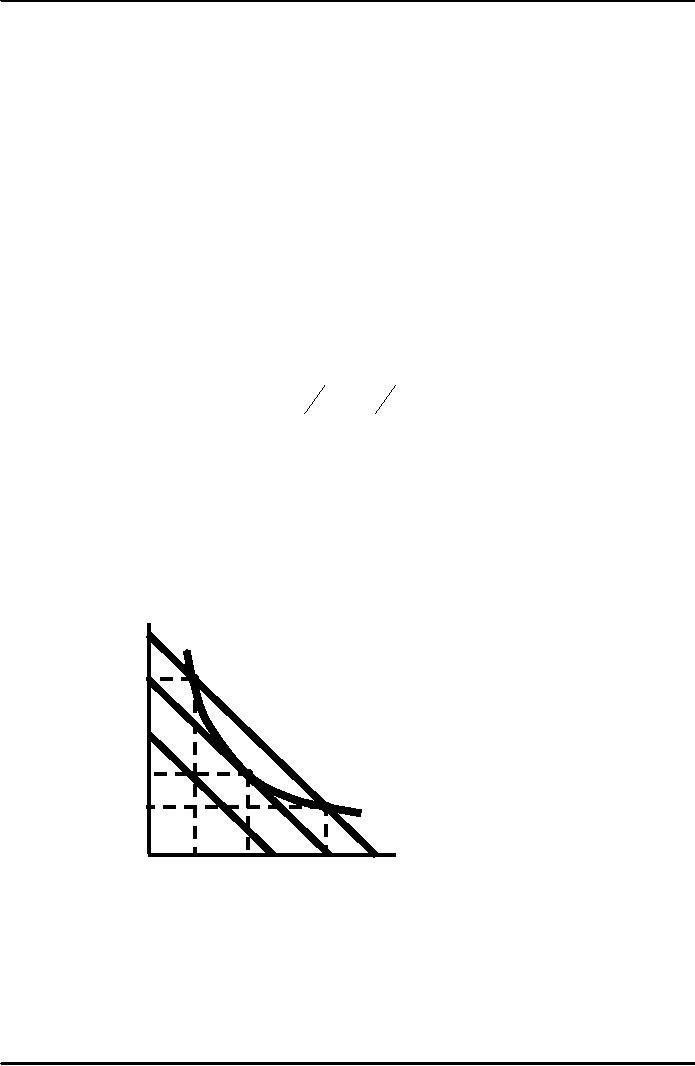
Producing
a Given Output at Minimum
Cost
Q1 is an
isoquant
Capital
for
output Q1.
per
Isocost
curve C0 shows
year
all
combinations of K
and
L
K2
that
can not produce Q1 at
this
Isocost
C2 shows
quantity
CO C1
C2 are
Q1 can
be produced with
three
combination
K2L2 or
K3L3.
Isocost
lines
A
However,
both of these
K1
are
higher cost
combinations
than
K1L1.
Q1
K3
C0
C1
C2
L2
L1
L3
Labor
per year
97
Microeconomics
ECO402
VU
Input
Substitution When an Input Price
Change
Isoquants
and Isocosts and the
Production Function
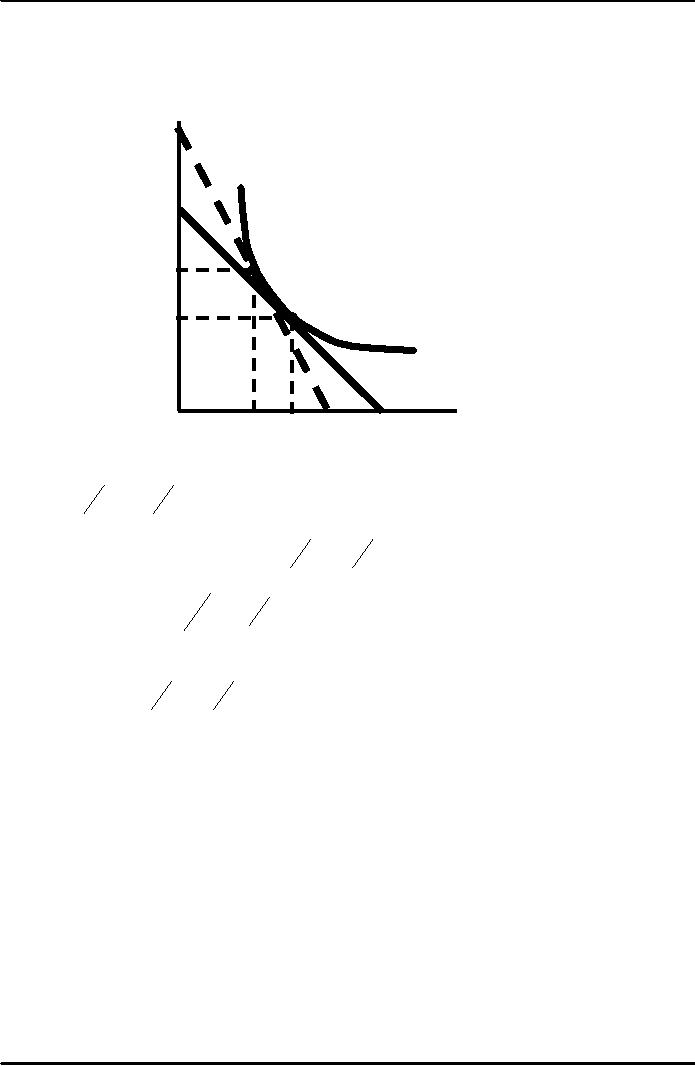
Capital
If
the price of labor
changes,
the Isocost curve
per
becomes
steeper due to
year
the
change in the slope -(w/L).
This
yields a new
combination
of
K
and
L
to
produce Q1.
Combination
B
is
used in place
B
of
combination A.
K2
The
new combination
represents
the
higher cost of labor
relative
A
to
capital and therefore
capital
K1
is
substituted for labor.
Q1
C2
C1
L2
Labor
per year
L1
MRTS
=
-ΔK
=
MPL
ΔL
MPK
Slope
of isocost line =
ΔK
=
-w
ΔL
r
MPL
=w
and
=
MPK
r
The
minimum cost combination can
then be written as:
MPL
=
MPK
w
r
Minimum cost
for a given output will
occur when each dollar of
input added to the
production
process will add an
equivalent amount of
output.
Question
If w = $10, r =
$2, and MPL
= MPK,
which input would the
producer use more of?
Why?
The
Effect of Effluent Fees on
Firms' Input
Choices
The
Effect of Effluent Fees on
Firms' Input
Choices
Firms
that have a by-product to
production produce an
effluent.
An
effluent fee is a per-unit
fee that firms must
pay for the effluent
that they emit.
How
would a producer respond to an
effluent fee on
production?
The
Scenario: Steel
Producer
98
Microeconomics
ECO402
VU
1)
Located on a river: Low cost
transportation and emission
disposal
(effluent).
2)
EPA imposes a per unit
effluent fee to reduce the
environmentally harmful
effluent.
3)
How should the firm
respond?
The
Cost-Minimizing Response to an Effluent
Fee
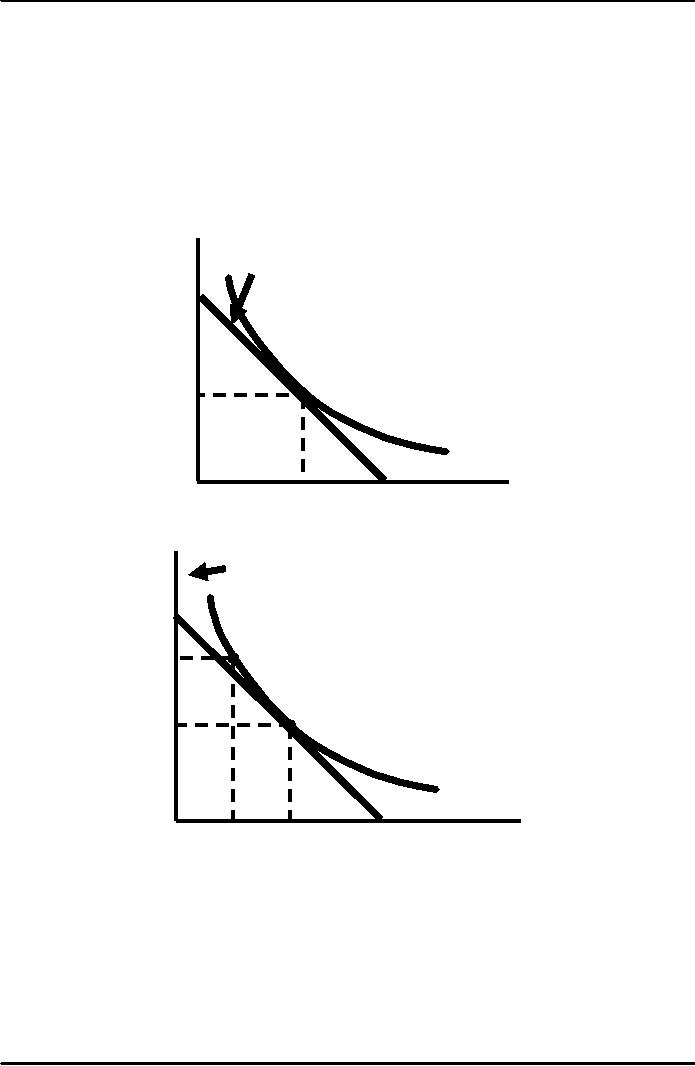
Capital
(machine
Slope
of
hours
per
Isocost
= -10/40
5,000
month)
=
-0.25
4,000
3,000
A
2,000
Output
of 2,000
1,000
Tons
of Steel per
Month
Waste
Water
5,000
10,000
12,000 18,000
20,000
0
(gal./month)
Capital
(machine
Prior
to regulation the
Slope
of
hours
per
firm
chooses to produce
Isocost
= -
month)
an
output using 10,000
20/40
5,000
gallons
of water and 2,000
=
-0.50
machine-hours
of capital at A.
F
4,000
Following
the imposition
B
of
the effluent fee of $10/gallon
3,500
the
slope of the Isocost changes
3,000
which
the higher cost of water
to
capital
so now combination B
A
is
selected.
2,000
1,000
Output
of 2,000
Tons
of Steel per
Month
C
E
Waste
Water
0
5,000
(gal./month)
10,000
12,000 18,000
20,000
Observations:
The more
easily factors can be
substituted; the more
effective the fee is in
reducing the
effluent.
The
greater the degree of
substitutes, the less the
firm will have to pay
(e.g.: $50,000 with
combination
B instead of $100,000 with
combination A).
99
Table of Contents:
- ECONOMICS:Themes of Microeconomics, Theories and Models
- Economics: Another Perspective, Factors of Production
- REAL VERSUS NOMINAL PRICES:SUPPLY AND DEMAND, The Demand Curve
- Changes in Market Equilibrium:Market for College Education
- Elasticities of supply and demand:The Demand for Gasoline
- Consumer Behavior:Consumer Preferences, Indifference curves
- CONSUMER PREFERENCES:Budget Constraints, Consumer Choice
- Note it is repeated:Consumer Preferences, Revealed Preferences
- MARGINAL UTILITY AND CONSUMER CHOICE:COST-OF-LIVING INDEXES
- Review of Consumer Equilibrium:INDIVIDUAL DEMAND, An Inferior Good
- Income & Substitution Effects:Determining the Market Demand Curve
- The Aggregate Demand For Wheat:NETWORK EXTERNALITIES
- Describing Risk:Unequal Probability Outcomes
- PREFERENCES TOWARD RISK:Risk Premium, Indifference Curve
- PREFERENCES TOWARD RISK:Reducing Risk, The Demand for Risky Assets
- The Technology of Production:Production Function for Food
- Production with Two Variable Inputs:Returns to Scale
- Measuring Cost: Which Costs Matter?:Cost in the Short Run
- A Firm’s Short-Run Costs ($):The Effect of Effluent Fees on Firms’ Input Choices
- Cost in the Long Run:Long-Run Cost with Economies & Diseconomies of Scale
- Production with Two Outputs--Economies of Scope:Cubic Cost Function
- Perfectly Competitive Markets:Choosing Output in Short Run
- A Competitive Firm Incurring Losses:Industry Supply in Short Run
- Elasticity of Market Supply:Producer Surplus for a Market
- Elasticity of Market Supply:Long-Run Competitive Equilibrium
- Elasticity of Market Supply:The Industry’s Long-Run Supply Curve
- Elasticity of Market Supply:Welfare loss if price is held below market-clearing level
- Price Supports:Supply Restrictions, Import Quotas and Tariffs
- The Sugar Quota:The Impact of a Tax or Subsidy, Subsidy
- Perfect Competition:Total, Marginal, and Average Revenue
- Perfect Competition:Effect of Excise Tax on Monopolist
- Monopoly:Elasticity of Demand and Price Markup, Sources of Monopoly Power
- The Social Costs of Monopoly Power:Price Regulation, Monopsony
- Monopsony Power:Pricing With Market Power, Capturing Consumer Surplus
- Monopsony Power:THE ECONOMICS OF COUPONS AND REBATES
- Airline Fares:Elasticities of Demand for Air Travel, The Two-Part Tariff
- Bundling:Consumption Decisions When Products are Bundled
- Bundling:Mixed Versus Pure Bundling, Effects of Advertising
- MONOPOLISTIC COMPETITION:Monopolistic Competition in the Market for Colas and Coffee
- OLIGOPOLY:Duopoly Example, Price Competition
- Competition Versus Collusion:The Prisoners’ Dilemma, Implications of the Prisoners
- COMPETITIVE FACTOR MARKETS:Marginal Revenue Product
- Competitive Factor Markets:The Demand for Jet Fuel
- Equilibrium in a Competitive Factor Market:Labor Market Equilibrium
- Factor Markets with Monopoly Power:Monopoly Power of Sellers of Labor