 |
Describing Risk:Unequal Probability Outcomes |
| << The Aggregate Demand For Wheat:NETWORK EXTERNALITIES |
| PREFERENCES TOWARD RISK:Risk Premium, Indifference Curve >> |

Microeconomics
ECO402
VU
Lesson
13
Introduction
Choice
with certainty is reasonably
straightforward.
How
do we choose when certain
variables such as income and
prices are uncertain
(i.e.
making
choices with risk)?
Describing
Risk
To
measure risk we must
know:
1)
All of the possible
outcomes.
2)
The likelihood that each
outcome will occur (its
probability).
Interpreting
Probability
The likelihood
that a given outcome will
occur
Objective
Interpretation
�
Based on the
observed frequency of past
events
Subjective
�
Based on
perception or experience with or
without an observed
frequency
Different
information or different abilities to
process the same information
can
influence
the subjective
probability
Expected
Value
The weighted
average of the payoffs or
values resulting from all
possible outcomes.
�
The
probabilities of each outcome
are used as weights
�
Expected value
measures the central
tendency; the payoff or
value expected on
average
An
Example
�
Investment in
drilling exploration:
�
Two outcomes
are possible
Success --
the stock price increase
from $30 to $40/share
Failure --
the stock price falls
from $30 to $20/share
�
Objective
Probability
100
explorations, 25 successes and 75
failures
Probability
(Pr) of success = 1/4 and
the probability of failure =
3/4
EV
=
Pr(success)($40/share)
+
Pr(failure)($20/share)
=
1
4 ($ 4 0 /s h a re ) +
3 4
($ 2 0 /s h a re )
EV
E
V =
$ 2 5
/s h a re
Given:
Two possible
outcomes having payoffs X1 and
X2
Probabilities of
each outcome is given by Pr1 & Pr2
Generally,
expected value is written
as:
E(X)
=
Pr1X1
+
Pr2X2
+...
+
Prn Xn
63

Microeconomics
ECO402
VU
Variability
The extent to
which possible outcomes of an
uncertain event may
differ
Variability:
A Scenario
Suppose you
are choosing between two
part-time sales jobs that
have the same
expected
income ($1,500)
The first
job is based entirely on
commission.
The second is a
salaried position.
There are
two equally likely outcomes
in the first job--$2,000 for
a good sales job
and
$1,000
for a modestly successful
one.
The second
pays $1,510 most of the
time (.99 probability), but
you will earn $510 if
the
company
goes out of business (.01
probability).
Income
from Sales Jobs
Outcome
1
Outcome
2
Probability
Income($)
probability
Income($)
Expected
income
.5
2000
.5
1000
1500
Job
1: Commission
.99
1510
.01
510
1500
Job
2: Fixed salary
E(X1 )
= .5($2000)
+
.5($1000)
=
$1500
Job
2 Expected Income
E(X
2 ) =
.99($1510)
+
.01($510)
=
$1500
While
the expected values are
the same, the variability is
not.
Greater
variability from expected
values signals greater
risk.
Deviation
Difference
between expected payoff and
actual payoff
Deviations
from Expected Income
($)
Outcome
1
Deviation
Outcome
2
Deviation
Job
1
$2,000
$500
$1,000
-$500
Job
2
1,510
10
510
-900
Adjusting
for negative numbers
The
standard deviation measures
the square root of the
average of the squares of
the
deviations
of the payoffs associated
with each outcome from
their expected value.
The
standard deviation is
written:
σ
= Pr[X1 -E(X)2]
+Pr
[X2 -E(X)2]
1
2
64
Microeconomics
ECO402
VU
Calculating
Variance ($)
Deviation
Deviation
Deviation
Standard
Outcome
1
Squared
Outcome
2
Squared
Squared
Deviation
Job
1 $2,000
$250,000
$1,000
$250,000
$250,000
$500.00
Job
2 1,510
100
510
980,100
9,900
99.50
The
standard deviations of the
two jobs are:
σ1
=
0)
+
.5($250,00
.5($250,00
0
σ
1
=
$
250 , 000
σ
1
=
500
*Greater
Risk
σ
=
+
.01($980,1
.99($100
00)
2
σ
=
$
9 , 900
2
σ
=
99 .
50
2
The
standard deviation can be
used when there are
many outcomes instead of
only two.
An
Example
Job 1 is a job
in which the income ranges
from $1000 to $2000 in
increments of $100
that
are all equally
likely.
Job 2 is a job
in which the income ranges
from $1300 to $1700 in
increments of $100
that,
also, are all equally
likely.
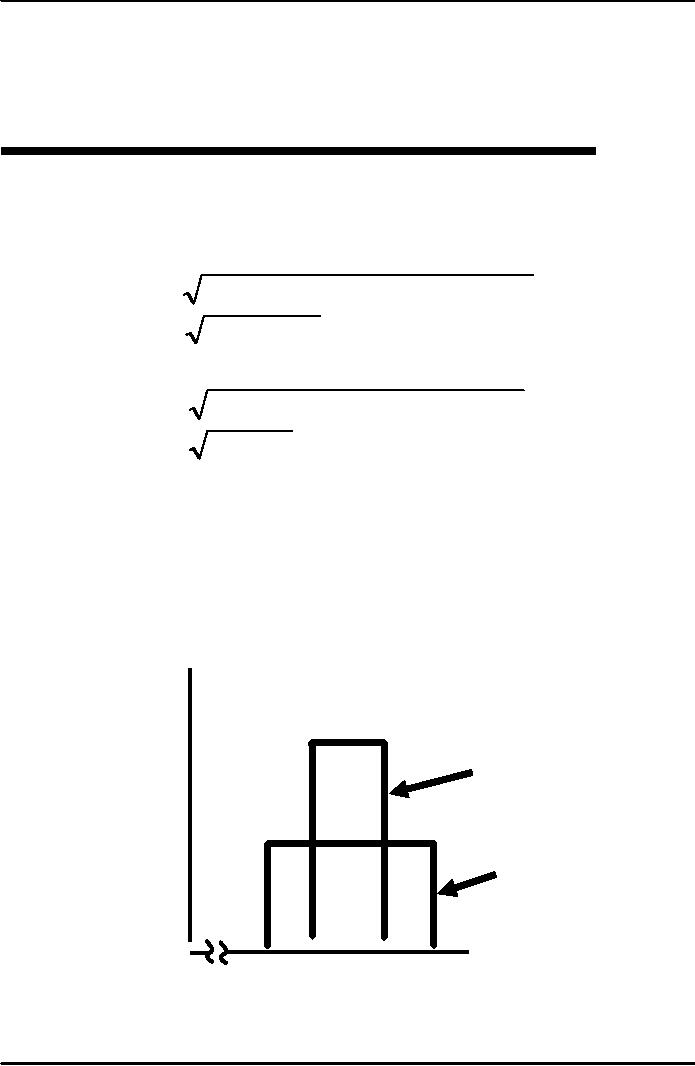
Probability
Job
1 has greater
spread:
greater
standard
deviation
and
greater risk
than
Job 2.
0.2
Job
2
0.1
Job
1
Income
$1000
$1500
$2000
Outcome
Probabilities of Two Jobs
(unequal probability of
outcomes)
Job 1: greater
spread & standard
deviation
65
Microeconomics
ECO402
VU
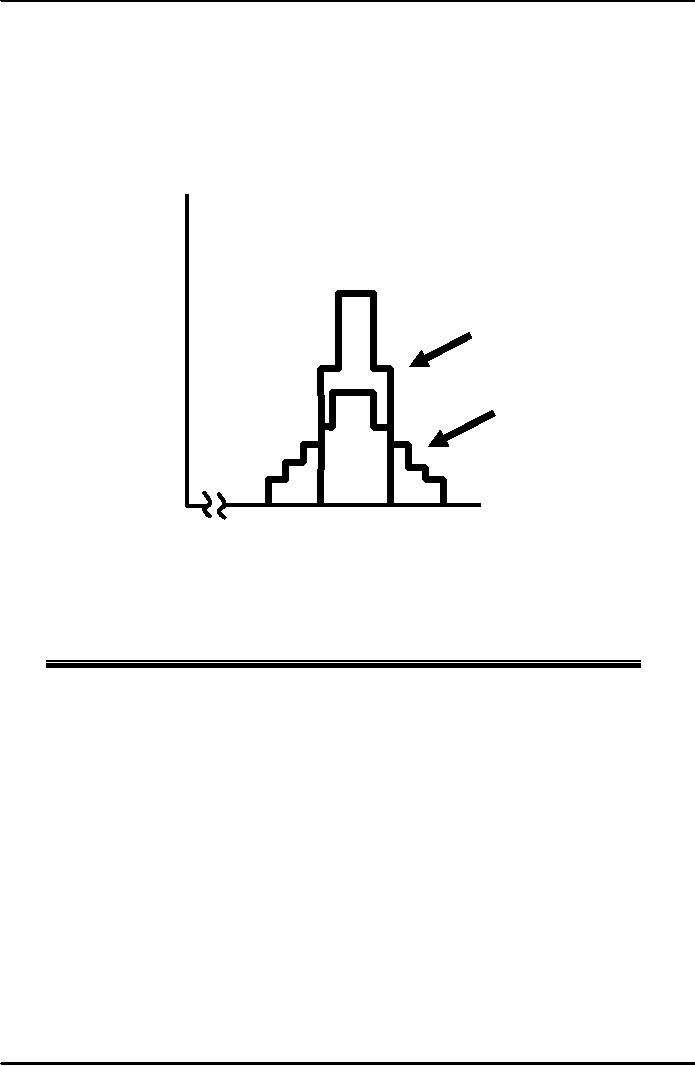
Peaked
distribution: extreme payoffs
are less likely
Decision
Making
A risk avoider
would choose Job 2: same
expected income as Job 1
with less risk.
Suppose we add
$100 to each payoff in Job 1
which makes the expected
payoff =
$1600.
Unequal
Probability Outcomes
The
distribution of payoffs
Probability
associated
with Job 1 has a
greater
spread and standard
deviation
than those with Job
2.
0.2
Job
2
0.1
Job
1
Income
$1000
$1500
$2000
Income
from Sales Jobs--Modified
($)
Deviation
Deviation
Deviation
Standard
Outcome
1
Squared
Outcome
2
Squared
Squared
Deviation
Job
1 $2,100
$250,000
$1,100
$250,000
$1,
600
$500
Job
2 1510
100
510
980,100
1,
500
99.50
Recall:
The standard deviation is
the square root of the
deviation squared.
Decision
making
Job 1: expected
income $1,600 and a standard
deviation of $500.
Job 2: expected
income of $1,500 and a
standard deviation of
$99.50
Which
job?
�
Greater
value or less risk?
Example
Suppose a city
wants to deter people from
wrong parking.
The
alternatives ......
66

Microeconomics
ECO402
VU
Assumptions:
1)
Wrong parking saves a person
$5 in terms of time spent
searching for a parking
space.
2)
The driver is risk
neutral.
3)
Cost of apprehension is
zero.
A
fine of $5.01 would deter
the driver from double
parking.
Benefit of
wrong parking ($5) is less
than the cost ($5.01)
equals a net benefit that
is
less
than 0.
Increasing
the fine can reduce
enforcement cost:
A $50 fine
with a .1 probability of being
caught results in an expected
penalty of $5.
A $500 fine
with a .01 probability of
being caught results in an
expected penalty of
$5.
The
more risk averse drivers
are, the lower the
fine needs to be in order to be
effective.
67
Table of Contents:
- ECONOMICS:Themes of Microeconomics, Theories and Models
- Economics: Another Perspective, Factors of Production
- REAL VERSUS NOMINAL PRICES:SUPPLY AND DEMAND, The Demand Curve
- Changes in Market Equilibrium:Market for College Education
- Elasticities of supply and demand:The Demand for Gasoline
- Consumer Behavior:Consumer Preferences, Indifference curves
- CONSUMER PREFERENCES:Budget Constraints, Consumer Choice
- Note it is repeated:Consumer Preferences, Revealed Preferences
- MARGINAL UTILITY AND CONSUMER CHOICE:COST-OF-LIVING INDEXES
- Review of Consumer Equilibrium:INDIVIDUAL DEMAND, An Inferior Good
- Income & Substitution Effects:Determining the Market Demand Curve
- The Aggregate Demand For Wheat:NETWORK EXTERNALITIES
- Describing Risk:Unequal Probability Outcomes
- PREFERENCES TOWARD RISK:Risk Premium, Indifference Curve
- PREFERENCES TOWARD RISK:Reducing Risk, The Demand for Risky Assets
- The Technology of Production:Production Function for Food
- Production with Two Variable Inputs:Returns to Scale
- Measuring Cost: Which Costs Matter?:Cost in the Short Run
- A Firm’s Short-Run Costs ($):The Effect of Effluent Fees on Firms’ Input Choices
- Cost in the Long Run:Long-Run Cost with Economies & Diseconomies of Scale
- Production with Two Outputs--Economies of Scope:Cubic Cost Function
- Perfectly Competitive Markets:Choosing Output in Short Run
- A Competitive Firm Incurring Losses:Industry Supply in Short Run
- Elasticity of Market Supply:Producer Surplus for a Market
- Elasticity of Market Supply:Long-Run Competitive Equilibrium
- Elasticity of Market Supply:The Industry’s Long-Run Supply Curve
- Elasticity of Market Supply:Welfare loss if price is held below market-clearing level
- Price Supports:Supply Restrictions, Import Quotas and Tariffs
- The Sugar Quota:The Impact of a Tax or Subsidy, Subsidy
- Perfect Competition:Total, Marginal, and Average Revenue
- Perfect Competition:Effect of Excise Tax on Monopolist
- Monopoly:Elasticity of Demand and Price Markup, Sources of Monopoly Power
- The Social Costs of Monopoly Power:Price Regulation, Monopsony
- Monopsony Power:Pricing With Market Power, Capturing Consumer Surplus
- Monopsony Power:THE ECONOMICS OF COUPONS AND REBATES
- Airline Fares:Elasticities of Demand for Air Travel, The Two-Part Tariff
- Bundling:Consumption Decisions When Products are Bundled
- Bundling:Mixed Versus Pure Bundling, Effects of Advertising
- MONOPOLISTIC COMPETITION:Monopolistic Competition in the Market for Colas and Coffee
- OLIGOPOLY:Duopoly Example, Price Competition
- Competition Versus Collusion:The Prisoners’ Dilemma, Implications of the Prisoners
- COMPETITIVE FACTOR MARKETS:Marginal Revenue Product
- Competitive Factor Markets:The Demand for Jet Fuel
- Equilibrium in a Competitive Factor Market:Labor Market Equilibrium
- Factor Markets with Monopoly Power:Monopoly Power of Sellers of Labor