Functional Dependency, Inference Rules, Normal Forms

<< Types of Joins: Theta Join, Equi–Join, Natural Join, Outer Join, Semi Join

Second, Third Normal Form, Boyce - Codd Normal Form, Higher Normal Forms >>

Database Management System (CS403)

Lecture No. 19

Reading Material

"Database Systems Principles, Design and Implementation"

Section 7.1 7.7

written by Catherine Ricardo, Maxwell Macmillan.

"Database Management Systems", 2nd edition, Raghu Ramakrishnan, Johannes Gehrke,

McGraw-Hill

Overview of Lecture:

o Functional Dependency

o Inference Rules

o Normal Forms

In the previous lecture we have studied different types of joins, which are used to

connect two different tables and give different output relations. We also started the

basics of normalization. From this lecture we will study in length different aspects of

normalization.

Functional Dependency

Normalization is based on the concept of functional dependency. A functional

dependency is a type of relationship between attributes.

164

Database Management System (CS403)

Definition of Functional Dependency

If A and B are attributes or sets of attributes of relation R, we say that B is

functionally dependent on A if each value of A in R has associated with it exactly one

value of B in R.

We write this as A

B, read as "A functionally determines B" or " A determines B".

This does not mean that A causes B or that the value of B can be calculated from the

value of A by a formula, although sometimes that is the case. It simply means that if

we know the value of A and we examine the table of relation R, we will find only one

value of B in all the rows that have the given value of A at any one time. Thus then

the two rows have the same A value, they must also have the same B value. However,

for a given B value, there may be several different A values. When a functional

dependency exits, the attributes or set of attributes on the left side of the arrow is

called a determinant. Attribute of set of attributes on left side are called determinant

and on right are called dependants. If there is a relation R with attributes (a,b,c,d,e)

b,c,d

For Example there is a relation of student with following attributes. We will establish

the functional dependency of different attributes: -

STD (stId,stName,stAdr,prName,credits)

stId

stName,stAdr,prName,credits

prName

credits

Now in this example if we know the stID we can tell the complete information about

that student. Similarly if we know the prName , we can tell the credit hours for any

particular subject.

Functional Dependencies and Keys:

We can determine the keys of a relation after seeing its functional dependencies. The

determinant of functional dependency that determines all attributes of that table is the

super key. Super key is an attribute or a set of attributes that identifies an entity

uniquely. In a table, a super key is any column or set of columns whose values can be

used to distinguish one row from another. A minimal super key is the candidate key ,

so if a determinant of functional dependency determines all attributes of that relation

then it is definitely a super key and if there is no other functional dependency whereas

a subset of this determinant is a super key then it is a candidate key. So the functional

dependencies help to identify keys. We have an example as under: -

EMP (eId,eName,eAdr,eDept,prId,prSal)

eId

(eName,eAdr,eDept)

eId,prId

prSal

Now in this example in the employee relation eId is the key from which we can

uniquely determine the employee name address and department . Similarly if we

know the employee ID and project ID we can find the project salary as well. So FDs

help in finding out the keys and their relation as well.

165

Database Management System (CS403)

Inference Rules

Rules of Inference for functional dependencies, called inference axioms or Armstrong

axioms, after their developer, can be used to find all the FDs logically implied by a set

of FDs.These rules are sound , meaning that they are an immediate consequence of

the definition of functional dependency and that any FD that can be derived from a

given set of FDs using them is true. They are also complete, meaning they can be used

to derive every valid reference about dependencies .Let A,B,C and D be subsets of

attributes of a relation R then following are the different inference rules: -

Reflexivity:

If B is a subset of A, then A

B. This also implies that A

A always holds.

Functional dependencies of this type are called trivial dependencies. For Example

StName,stAdr

stName

Augmentation:

If we have A

B then AC.

BC. For Example

If stId

stName then

StId,stAdr

stName,stadr

Transitivity:

If A

B and B

C, then A

If stId

prName and prName

credits then

stId

credits

Additivity or Union:

If A

B and A

C, then A

If empId

eName and empId

qual Then we can write it as

empId

qual

Projectivity or Decomposition

If A

BC then A

B and A

If empId

eName,qual Then we can write it as

empId

eName and empID

qual

Pseudo transitivity:

If A

B and CB

D, then AC

If stID

stName and stName,fName

stAdr Then we can write it as

StId,fName

stAdr

Normal Forms

Normalization is basically; a process of efficiently organizing data in a database.

There are two goals of the normalization process: eliminate redundant data (for

example, storing the same data in more than one table) and ensure data dependencies

make sense (only storing related data in a table). Both of these are worthy goals as

they reduce the amount of space a database consumes and ensure that data is logically

stored. We will now study the first normal form

166

Database Management System (CS403)

First Normal Form:

A relation is in first normal form if and only if every attribute is single valued for each

tuple. This means that each attribute in each row , or each cell of the table, contains

only one value. No repeating fields or groups are allowed. An alternative way of

describing first normal form is to say that the domains of attributes of a relation are

atomic, that is they consist of single units that cannot be broken down further. There

is no multivalued (repeating group) in the relation multiple values create problems in

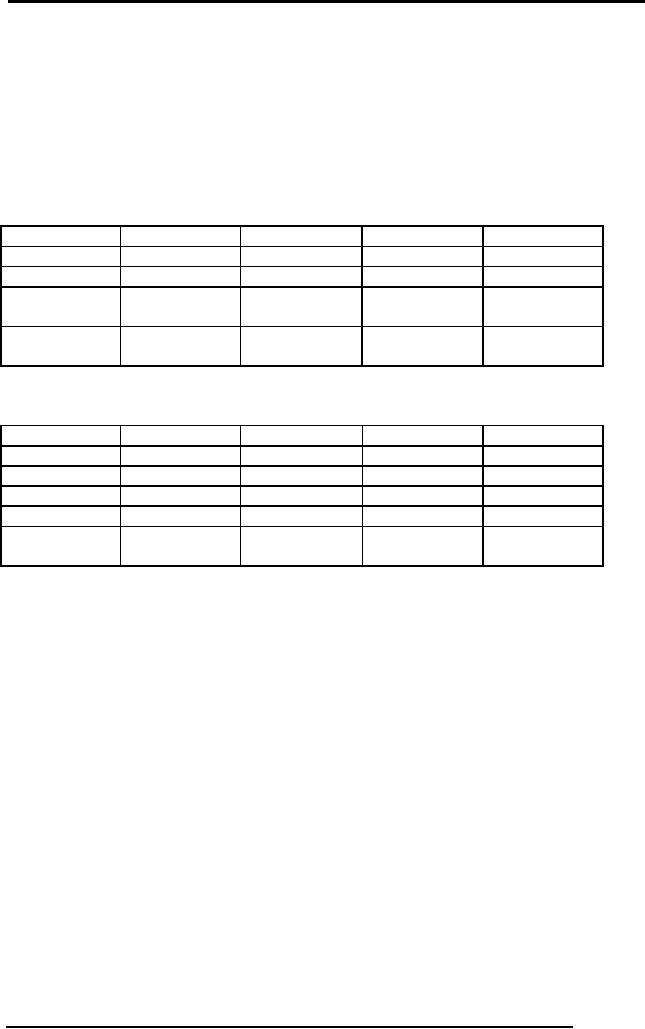
performing operations like select or join. For Example there is a relation of Student

STD(stIdstName,stAdr,prName,bkId)

stId

stName

stAdr

prName

bkId

S1020

Sohail Dar

I-8 Islamabad

MCS

B00129

S1038

Shoaib Ali

G-6 Islamabad

BCS

B00327

S1015

Tahira Ejaz

L Rukh Wah

MCS

B08945,

B06352

S1018

Arif Zia

E-8,

BIT

B08474

Islamabad.

Now in this table there is no unique value for every tuple, like for S1015 there are two

values for bookId. So to bring it in the first normal form.

stId

stName

stAdr

prName

bkId

S1020

Sohail Dar

I-8 Islamabad

MCS

B00129

S1038

Shoaib Ali

G-6 Islamabad BCS

B00327

S1015

Tahira Ejaz

L Rukh Wah

MCS

B08945

S1015

Tahira Ejaz

L Rukh Wah

MCS

B06352

S1018

Arif Zia

E-8,

BIT

B08474

Islamabad.

Now this table is in first normal form and for every tuple there is a unique value.

Second Normal Form:

A relation is in second normal form (2NF) if and only if it is in first normal form and

all the nonkey attributes are fully functionally dependent on the key. Clearly, if a

relation is in 1NF and the key consists of a single attribute, the relation is

automatically in 2NF. The only time we have to be concerned about 2NF is when the

key is composite. Second normal form (2NF) addresses the concept of removing

duplicative data. It remove subsets of data that apply to multiple rows of a table and

place them in separate tables. It creates relationships between these new tables and

their predecessors through the use of foreign keys.

Summary

Normalization is the process of structuring relational database schema such that most

ambiguity is removed. The stages of normalization are referred to as normal forms

and progress from the least restrictive (First Normal Form) through the most

restrictive (Fifth Normal Form). Generally, most database designers do not attempt to

implement anything higher than Third Normal Form or Boyce-Codd Normal Form.

167

Database Management System (CS403)

We have started the process of normalization in this lecture. We will cover this topic

in detail in the coming lectures.

Exercise:

Draw the tables of an examination system along with attributes and bring those

relations in First Normal Form.

168

Table of Contents: