Types of Joins: Theta Join, Equiâ€“Join, Natural Join, Outer Join, Semi Join

<< The Project Operator

Functional Dependency, Inference Rules, Normal Forms >>

Database Management System (CS403)

Lecture No. 18

Reading Material

"Database Systems Principles, Design and Implementation"

Section 6.6.1 6.6.3

written by Catherine Ricardo, Maxwell Macmillan.

Overview of Lecture:

o Types of Joins

o Relational Calculus

o Normalization

In the previous lecture we have studied the basic operators of relational algebra along

with different examples. From this lecture we will study the different types of joins,

which are very important and are used extensively in relational calculus.

Types of Joins

Join is a special form of cross product of two tables. It is a binary operation that

allows combining certain selections and a Cartesian product into one operation. The

join operation forms a Cartesian product of its two arguments, performs a selection

forcing equality on those attributes that appear in both relation schemas, and finally

removes duplicate attributes. Following are the different types of joins: -

1. Theta Join

2. Equi Join

3. Semi Join

4. Natural Join

5. Outer Joins

We will now discuss them one by one

Theta Join:

In theta join we apply the condition on input relation(s) and then only those selected

rows are used in the cross product to be merged and included in the output. It means

that in normal cross product all the rows of one relation are mapped/merged with all

the rows of second relation, but here only selected rows of a relation are made cross

product with second relation. It is denoted as under: -

RX S

157

Database Management System (CS403)

If R and S are two relations then is the condition, which is applied for select

operation on one relation and then only selected rows are cross product with all the

rows of second relation. For Example there are two relations of FACULTY and

COURSE, now we will first apply select operation on the FACULTY relation for

selection certain specific rows then these rows will have across product with

COURSE relation, so this is the difference in between cross product and theta join.

We will now see first both the relation their different attributes and then finally the

cross product after carrying out select operation on relation.

From this example the difference in between cross product and theta join becomes

clear.

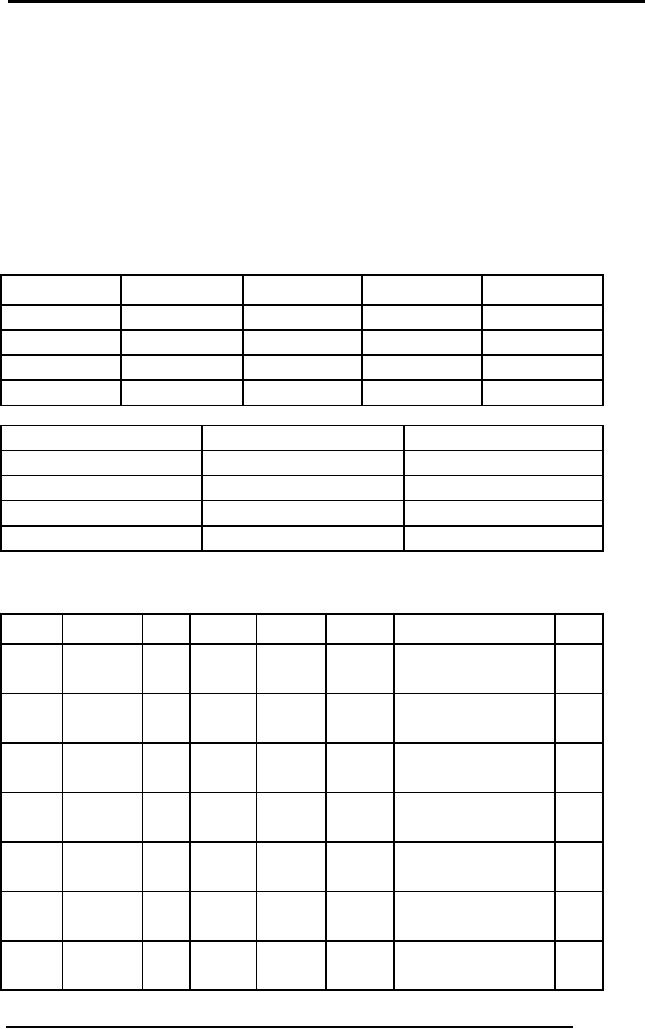
FACULTY

facId

facName

dept

salary

rank

F234

Usman

CSE

21000

lecturer

F235

Tahir

CSE

23000

Asso Prof

F236

Ayesha

ENG

27000

Asso Prof

F237

Samad

ENG

32000

Professor

COURSE

crCode

crTitle

fId

C3456

Database Systems

F234

C3457

Financial Management

C3458

Money & Capital Market

F236

C3459

Introduction to Accounting

F237

(σ rank = `Asso Prof'(FACULTY)) X COURSE

facName dept salary

rank

crCode crTitle

fId

facId

F235

Tahir

CSE

23000

Asso

C3456

Database Systems

F234

Prof

F235

Tahir

CSE

23000

Asso

C3457

Financial Management

Prof

F235

Tahir

CSE

23000

Asso

C3458

Money & Capital Market

F236

Prof

F235

Tahir

CSE

23000

Asso

C3459

Introduction

F237

Prof

Accounting

F236

Ayesha

ENG

27000

Asso

C3456

Database Systems

F234

Prof

F236

Ayesha

ENG

27000

Asso

C3457

Financial Management

Prof

F236

Ayesha

ENG

27000

Asso

C3458

Money & Capital Market

F236

Prof

158

Database Management System (CS403)

F236

Ayesha

ENG

27000

Asso

C3459

Introduction

F237

Prof

Accounting

Fig. 1: Two tables with an example of theta join

In this example after fulfilling the select condition of Associate professor on faculty relation

then it is cross product with course relation

EquiJoin:

This is the most used type of join. In equijoin rows are joined on the basis of values

of a common attribute between the two relations. It means relations are joined on the

basis of common attributes between them; which are meaningful. This means on the

basis of primary key, which is a foreign key in another relation. Rows having the

same value in the common attributes are joined. Common attributes appear twice in

the output. It means that the attributes, which are common in both relations, appear

twice, but only those rows, which are selected. Common attribute with the same name

is qualified with the relation name in the output. It means that if primary and foreign

keys of two relations are having the same names and if we take the equi join of both

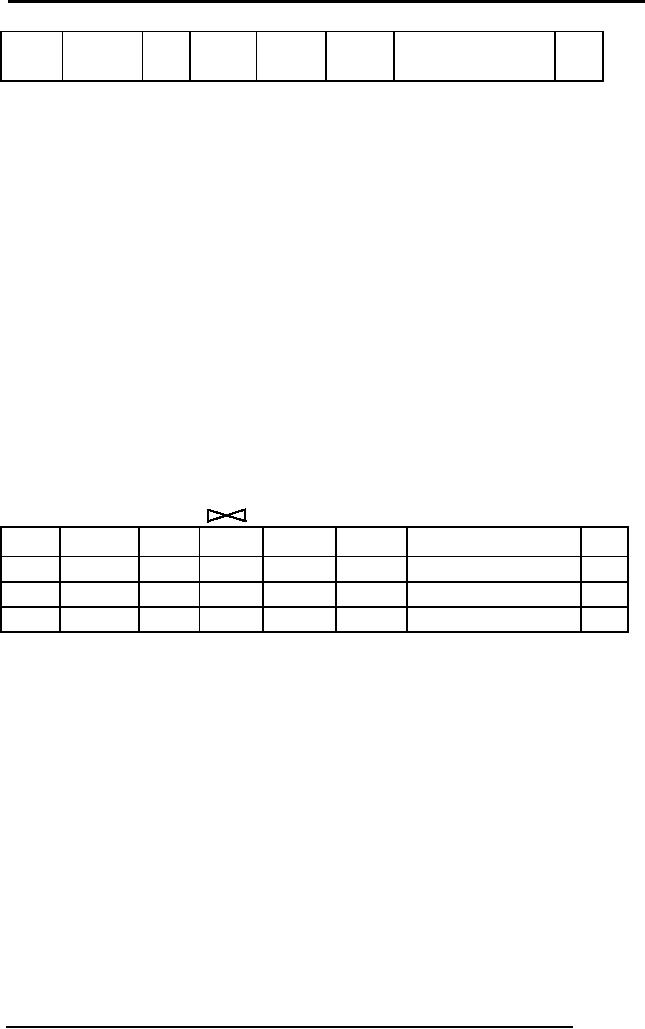
then in the output relation the relation name will precede the attribute name. For

Example, if we take the equi join of faculty and course relations then the output

would be as under: -

FACULTY..facId=COURSE.fId COURSE

FACULTY

facId facName dept

salary rank

crCode

crTitle

fID

F234

Usman

CSE

21000

lecturer

C3456

Database Systems

F234

F236

Ayesha

ENG

27000

Asso Prof

C3458

Money & Capital Market

F236

F237

Samad

ENG

32000

Professor

C3459

Introduction to Accounting

F237

Fig. 2: Equi-join on tables of figure 1

In the above example the name of common attribute between the two tables is

different, that is, it is facId in FACULTY and fId in COURSE, so it is not required to

qualify; however there is no harm doing it still. Now in this example after taking

equijoin only those tuples are selected in the output whose values are common in

both the relations.

Natural Join:

This is the most common and general form of join. If we simply say join, it means the

natural join. It is same as equijoin but the difference is that in natural join, the

common attribute appears only once. Now, it does not matter which common attribute

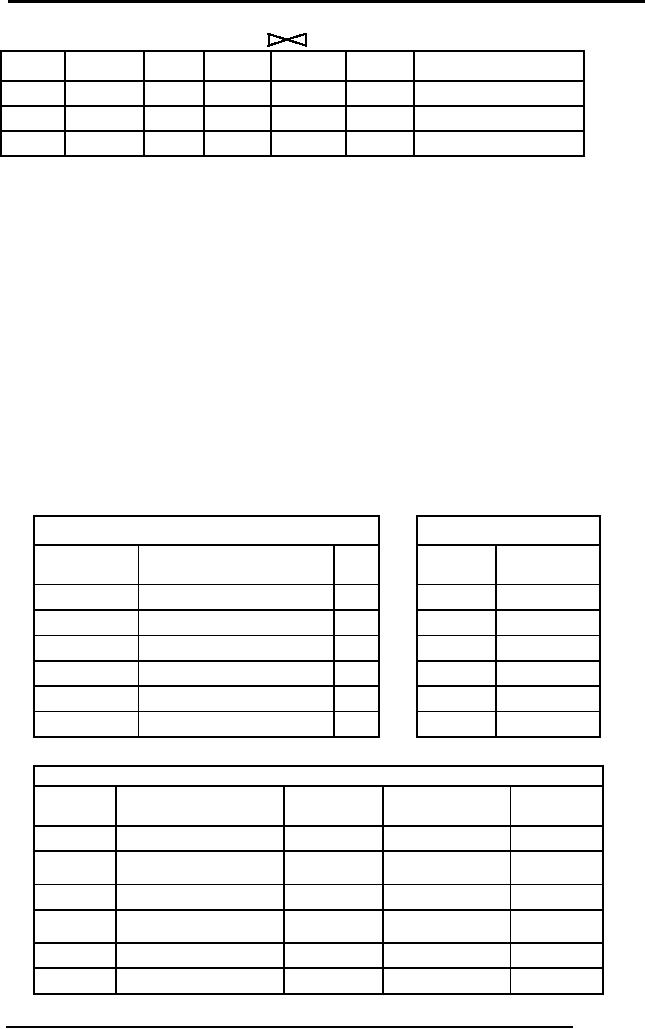
should be part of the output relation as the values in both are same. For Example if we

take the natural join of faculty and course the output would be as under: -

159

Database Management System (CS403)

FACULTY

facId, fId COURSE

facId

facName dept

salary

rank

crCode crTitle

F234

Usman

CSE

21000

Lecturer

C3456

Database Systems

F236

Ayesha

ENG

27000

Asso Prof

C3458

Money & Capital Market

F237

Samad

ENG

32000

Professor

C3459

Introduction to Accounting

Fig. 4: Natural join of FACULTY and COURSE tables of figure 1

In this example the common attribute appears only once, rest the behavior is same.

Following are the different types of natural join:-

Left Outer Join:

In left outer join all the tuples of left relation remain part of the output. The tuples that

have a matching tuple in the second relation do have the corresponding tuple from the

second relation. However, for the tuples of the left relation, which do not have a

matching record in the right tuple have Null values against the attributes of the right

relation. The example is given in figure 5 below. It can be described in another way.

Left outer join is the equi-join plus the non matching rows of the left side relation

having Null against the attributes of right side relation.

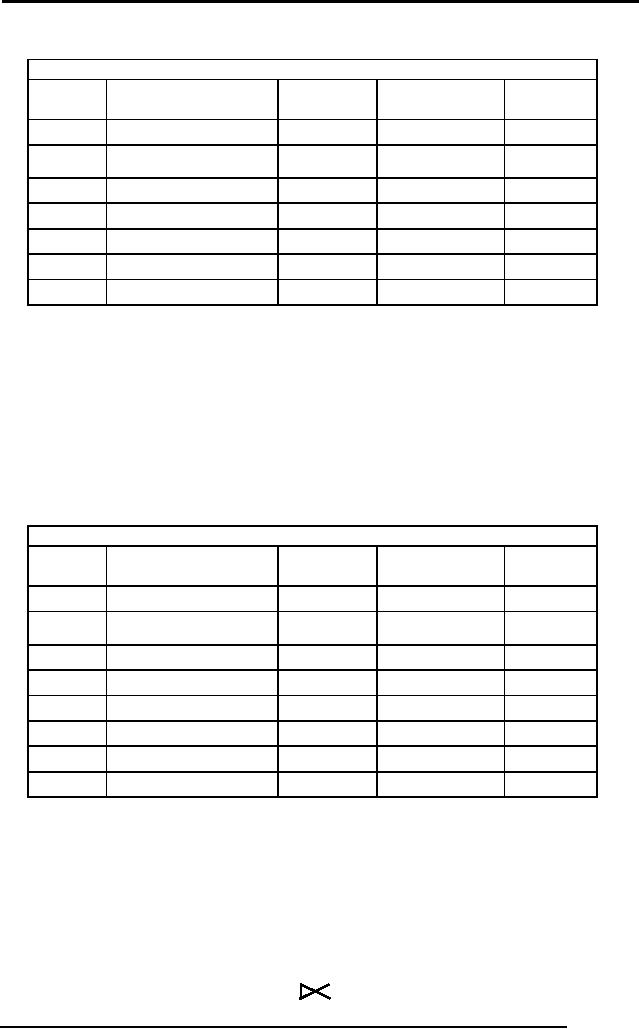
Right Outer Join:

In right outer join all the tuples of right relation remain part of the output relation,

whereas on the left side the tuples, which do not match with the right relation, are left

as null. It means that right outer join will always have all the tuples of right relation

and those tuples of left relation which are not matched are left as Null.

COURSE

STUDENT

stId

bkId

bkTitile

stId

stName

B10001

Intro to Database Systems

S104

S101

Ali Tahir

B10002

Programming Fundamentals

S101

S103

Farah Hasan

B10003

Intro Data Structures

S101

S104

Farah Naz

B10004

Modern Operating Systems

S103

S106

Asmat Dar

B10005

Computer Architecture

S107

Liaqat Ali

B10006

Advanced Networks

S104

COURSE left outer join STUDENT

bkId bkTitile

BOOK.stId STUDENT.stId

stName

B10001

Intro to Database Systems

S104

Farah Naz

B10002

Programming

S101

Ali Tahir

Fundamentals

B10003

Intro Data Structures

S101

Ali Tahir

B10004

Modern

Operating

S103

Farah Hasan

Systems

B10006

Advanced Networks

S104

Farah Naz

B10005

Computer Architecture

Null

160

Database Management System (CS403)

COURSE right outer join STUDENT

bkId bkTitile

BOOK.stId STUDENT.stId

stName

B10001

Intro to Database Systems

S104

Farah Naz

B10002

Programming

S101

Ali Tahir

Fundamentals

B10003

Intro Data Structures

S101

Ali Tahir

B10004

Modern Operating Systems

S103

Farah Hasan

B10006

Advanced Networks

S104

Farah Naz

Null

S106

Asmat Dar

Null

S107

Liaqat Ali

Fig. 5: Input tables and left outer join and right outer join

Outer Join:

In outer join all the tuples of left and right relations are part of the output. It means

that all those tuples of left relation which are not matched with right relation are left

as Null. Similarly all those tuples of right relation which are not matched with left

relation are left as Null.

COURSE outer join STUDENT

bkId bkTitile

BOOK.stId STUDENT.stId

stName

B10001

Intro to Database Systems

S104

Farah Naz

B10002

Programming

S101

Ali Tahir

Fundamentals

B10003

Intro Data Structures

S101

Ali Tahir

B10004

Modern Operating Systems

S103

Farah Hasan

B10006

Advanced Networks

S104

Farah Naz

B10005

Computer Architecture

Null

S106

Asmat Dar

Null

S107

Liaqat Ali

Fig. 6: outer join operation on tables of figure 5

Semi Join:

In semi join, first we take the natural join of two relations then we project the

attributes of first table only. So after join and matching the common attribute of both

relations only attributes of first relation are projected. For Example if we take the

semi join of two relations faculty and course then the resulting relation would be as

under:-

FACULTY

COURSE

161

Database Management System (CS403)

facId

facName Dept

Salary

Rank

F234

Usman

CSE

21000

lecturer

F236

Ayesha

ENG

27000

Asso Prof

F237

Samad

ENG

32000

Professor

Fig. 7: Semi-join operation on tables of figure 1

Now the resulting relation has attributes of first relation only after taking the natural

join of both relations.

Relational Calculus

Relational Calculus is a nonprocedural formal relational data manipulation language

in which the user simply specifies what data should be retrieved, but not how to

retrieve it. It is an alternative standard for relational data manipulation languages. The

relational calculus is not related to the familiar differential and integral calculus in

mathematics, but takes its name from a branch of symbolic logic called the predicate

calculus. It has two following two forms: -

· Tuple Oriented Relational Calculus

Domain Oriented Relational Calculus

Tuple Oriented Relational Calculus:

In tuple oriented relational calculus we are interested primarily in finding relation

tuples for which a predicate is true. To do so we need tuple variables. A tuple variable

is a variable that takes on only the tuples of some relation or relations as its range of

values. It actually corresponds to a mathematical domain. We specify the range of a

tuple variable by a statement such as: -

RANGE OF S IS STUDENT

Here, S is the tuple variable and STUDENT is the range, so that S always represents a

tuple of STUDENT. It is expressed as

{S | P (S)}

We will read it as find the set of all tuples S such that P(S) is true, where P implies the

predicate condition now suppose range of R is STUDENT

{R | R.Credits > 50}

We will say like find the stuId, stuName, majors etc of all students having more than

50 credits.

Domain Oriented Relational Calculus:

Normalization

There are four types of anomalies, which are of concern, redundancy, insertion,

deletion and updation. Normalization is not compulsory, but it is strongly

162

Database Management System (CS403)

recommended that normalization must be done. Because normalized design makes the

maintenance of database much easier. While carrying out the process of normalization,

it should be applied on each table of database. It is performed after the logical

database design. This process is also being followed informally during conceptual

database design as well.

Normalization Process

There are different forms or levels of normalization. They are called as first, second

and so on. Each normalized form has certain requirements or conditions, which must

be fulfilled. If a table or relation fulfills any particular form then it is said to be in that

normal form. The process is applied on each relation of the database. The minimum

form in which all the tables are in is called the normal form of entire database. The

main objective of normalization is to place the database in highest form of

normalization.

Summary

In this lecture we have studied the different types of joins, with the help of which we

can join different tables. We can get different types of outputs from joins. Then we

studied relational calculus in which we briefly touched upon tuple and domain

oriented relational calculus. Lastly we started the process of normalization which is a

very important topic and we will discuss in detail this topic in the coming lectures.

Exercise:

Draw two tables of PROJECT and EMPLOYEE along with different attribute, include

a common attribute between the two to implement the PK/FK relationship and

populate both the tables. Then apply all types of joins and observe the difference in

the output relations

163

Table of Contents: