ZeePedia

ECONOMIC GROWTH (Continued…):The Golden Rule, Policies to promote growth

<< ECONOMIC GROWTH (Continued…):The Golden Rule Capital Stock
ECONOMIC GROWTH (Continued…):Possible problems with industrial policy >>
img
Macroeconomics ECO 403
VU
LESSON 22
ECONOMIC GROWTH (Continued...)
Issues under Consideration
·
Technological progress in the Solow model
·
Policies to promote growth
·
Growth empirics:
Confronting the theory with facts
·
Endogenous growth:
Two simple models in which the rate of technological progress is endogenous
Introduction
Previously, in the Solow model
·  The production technology was held constant
·  Income per capita was constant in the steady state.
Neither point is true in the real world
Tech. progress in the Solow model
·
A new variable: E = labor efficiency
·
Assume:
Technological progress is labor-augmenting: it increases labor efficiency at the exogenous
rate g:
ΔE
g=
E
·
We now write the production function as:
Y = F (K , L × E )
Where L × E = the number of effective workers.
·
­  Hence, increases in labor efficiency have the same effect on output as
increases in the labor force.
·
Notation:
y = Y/LE = output per effective worker
k = K/LE = capital per effective worker
·
Production function per effective worker:
y = f(k)
·
Saving and investment per effective worker:
s y = s f(k)
88
img
Macroeconomics ECO 403
VU
(δ + n + g)k = break-even investment:
the amount of investment necessary to keep k constant.
Consists of:
δ k to replace depreciating capital
n k to provide capital for new workers
g k to provide capital for the new "effective" workers created by technological progress
Δk = s f(k) - (δ +n +g)k
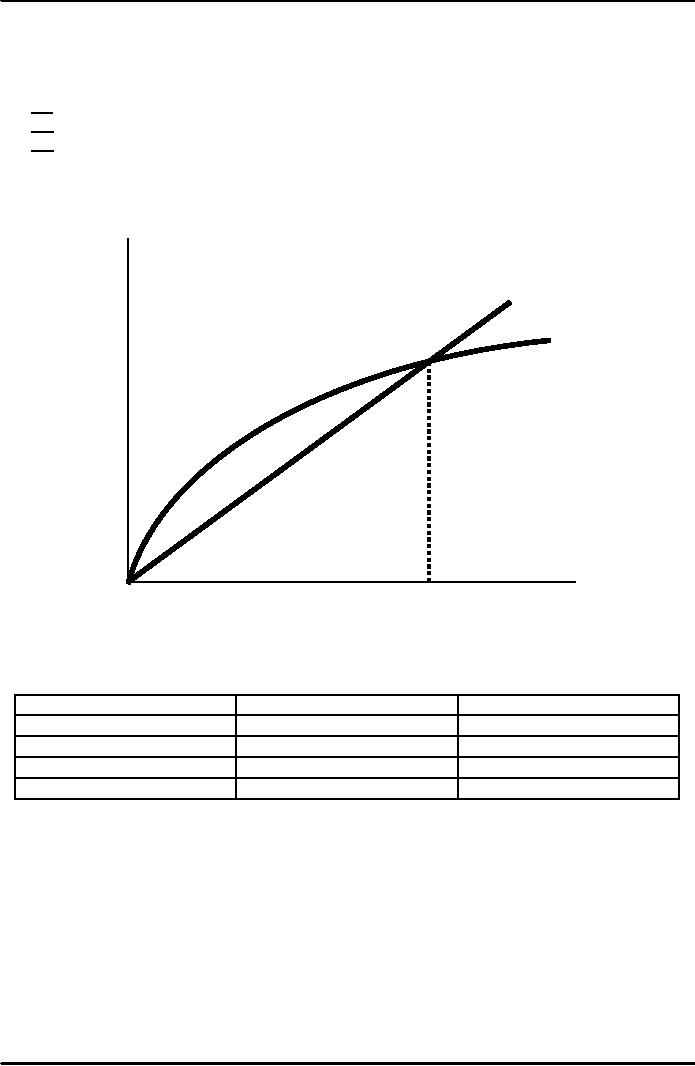
Investment, break-even
investment
(δ +n +g ) k
sf(k)
k*
Capital per
worker, k
Steady-State Growth Rates in the Solow Model with Tech. Progress
Variable
Symbol
Steady-Steady growth rate
k = K/ (L ×E )
Capital per effective worker
0
y = Y/ (L ×E )
Output per effective worker
0
(Y/ L ) = y ×E
Output per worker
g
Y = y ×E ×L
Total output
n+g
The Golden Rule
To find the Golden Rule capital stock,
express c* in terms of k*:
=  y* -  i*
c*
= f(k* ) - (δ + n + g) k*
c* is maximized when
MPK = δ + n + g
or equivalently,
MPK - δ = n + g
89
img
Macroeconomics ECO 403
VU
In the Golden Rule Steady State, the marginal product of capital net of depreciation equals the
population growth rate plus the rate of tech progress.
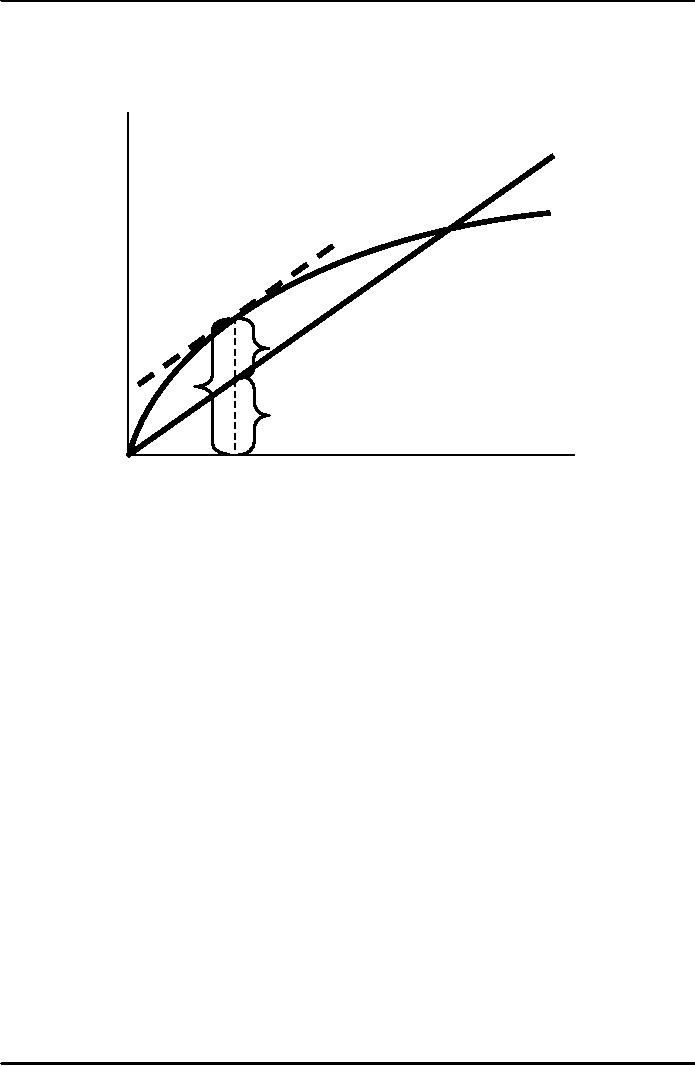
The Golden Rule Capital Stock
steady state
(δ +n+g) k*
output and
investment
f(k*)
C*gold
i*gold = (δ+ n+g)k*gold
k*gold
steady-state capital per
worker, k*
Policies to promote growth
Four policy questions:
·  Are we saving enough? Too much?
·  What policies might change the saving rate?
·  How should we allocate our investment between privately owned physical capital,
public infrastructure, and "human capital"?
·  What policies might encourage faster technological progress?
1. Evaluating the Rate of Saving
·
Use the Golden Rule to determine whether
our saving rate and capital stock are too high, too low, or about right.
·
To do this, we need to compare
(MPK - δ ) to (n + g).
· If (MPK - δ ) > (n + g), then we are below the Golden Rule steady state and should increase
s.
· If (MPK - δ ) < (n + g), then we are above the Golden Rule steady state and should reduce
s.
90
img
Macroeconomics ECO 403
VU
To estimate (MPK - δ ), we use three facts about an economy;
1. k = 2.5 y
the capital stock is about 2.5 times one year's GDP.
2. δ k = 0.1 y
about 10% of GDP is used to replace depreciating capital.
3. MPK × k = 0.3 y
Capital income is about 30% of GDP
So
1. k = 2.5 y
2. δ k = 0.1 y
3. MPK × k = 0.3 y
To determine δ , divided 2 by 1:
0.1
δk
0.1 y
⇒
δ =
= 0.04
=
2.5
k
2.5 y
To determine MPK, divided 3 by 1:
MPK × k
0.3 y
0.3
⇒
=
MPK =
= 0.12
k
2.5 y
2.5
Hence, MPK - δ = 0.12 - 0.04 = 0.08
·
Real GDP grows an average of 3%/year,
so n + g = 0.03
·
Thus, in this economy,
MPK - δ = 0.08 > 0.03 = n + g
Conclusion:
The economy is below the Golden Rule steady state:
if we increase saving rate of this economy, the economy will have faster growth until it
reaches to a new steady state with higher consumption per capita.
91
Table of Contents:
  1. INTRODUCTION:COURSE DESCRIPTION, TEN PRINCIPLES OF ECONOMICS
  2. PRINCIPLE OF MACROECONOMICS:People Face Tradeoffs
  3. IMPORTANCE OF MACROECONOMICS:Interest rates and rental payments
  4. THE DATA OF MACROECONOMICS:Rules for computing GDP
  5. THE DATA OF MACROECONOMICS (Continued…):Components of Expenditures
  6. THE DATA OF MACROECONOMICS (Continued…):How to construct the CPI
  7. NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES
  8. NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES (Continued…)
  9. NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES (Continued…)
  10. NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES (Continued…)
  11. MONEY AND INFLATION:The Quantity Equation, Inflation and interest rates
  12. MONEY AND INFLATION (Continued…):Money demand and the nominal interest rate
  13. MONEY AND INFLATION (Continued…):Costs of expected inflation:
  14. MONEY AND INFLATION (Continued…):The Classical Dichotomy
  15. OPEN ECONOMY:Three experiments, The nominal exchange rate
  16. OPEN ECONOMY (Continued…):The Determinants of the Nominal Exchange Rate
  17. OPEN ECONOMY (Continued…):A first model of the natural rate
  18. ISSUES IN UNEMPLOYMENT:Public Policy and Job Search
  19. ECONOMIC GROWTH:THE SOLOW MODEL, Saving and investment
  20. ECONOMIC GROWTH (Continued…):The Steady State
  21. ECONOMIC GROWTH (Continued…):The Golden Rule Capital Stock
  22. ECONOMIC GROWTH (Continued…):The Golden Rule, Policies to promote growth
  23. ECONOMIC GROWTH (Continued…):Possible problems with industrial policy
  24. AGGREGATE DEMAND AND AGGREGATE SUPPLY:When prices are sticky
  25. AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…):
  26. AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…):
  27. AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…)
  28. AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…)
  29. AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…)
  30. AGGREGATE DEMAND IN THE OPEN ECONOMY:Lessons about fiscal policy
  31. AGGREGATE DEMAND IN THE OPEN ECONOMY(Continued…):Fixed exchange rates
  32. AGGREGATE DEMAND IN THE OPEN ECONOMY (Continued…):Why income might not rise
  33. AGGREGATE SUPPLY:The sticky-price model
  34. AGGREGATE SUPPLY (Continued…):Deriving the Phillips Curve from SRAS
  35. GOVERNMENT DEBT:Permanent Debt, Floating Debt, Unfunded Debts
  36. GOVERNMENT DEBT (Continued…):Starting with too little capital,
  37. CONSUMPTION:Secular Stagnation and Simon Kuznets
  38. CONSUMPTION (Continued…):Consumer Preferences, Constraints on Borrowings
  39. CONSUMPTION (Continued…):The Life-cycle Consumption Function
  40. INVESTMENT:The Rental Price of Capital, The Cost of Capital
  41. INVESTMENT (Continued…):The Determinants of Investment
  42. INVESTMENT (Continued…):Financing Constraints, Residential Investment
  43. INVESTMENT (Continued…):Inventories and the Real Interest Rate
  44. MONEY:Money Supply, Fractional Reserve Banking,
  45. MONEY (Continued…):Three Instruments of Money Supply, Money Demand