 |
ECONOMIC GROWTH (Continued…):The Steady State |
| << ECONOMIC GROWTH:THE SOLOW MODEL, Saving and investment |
| ECONOMIC GROWTH (Continued…):The Golden Rule Capital Stock >> |
Macroeconomics
ECO 403
VU
LESSON
20
ECONOMIC
GROWTH (Continued...)
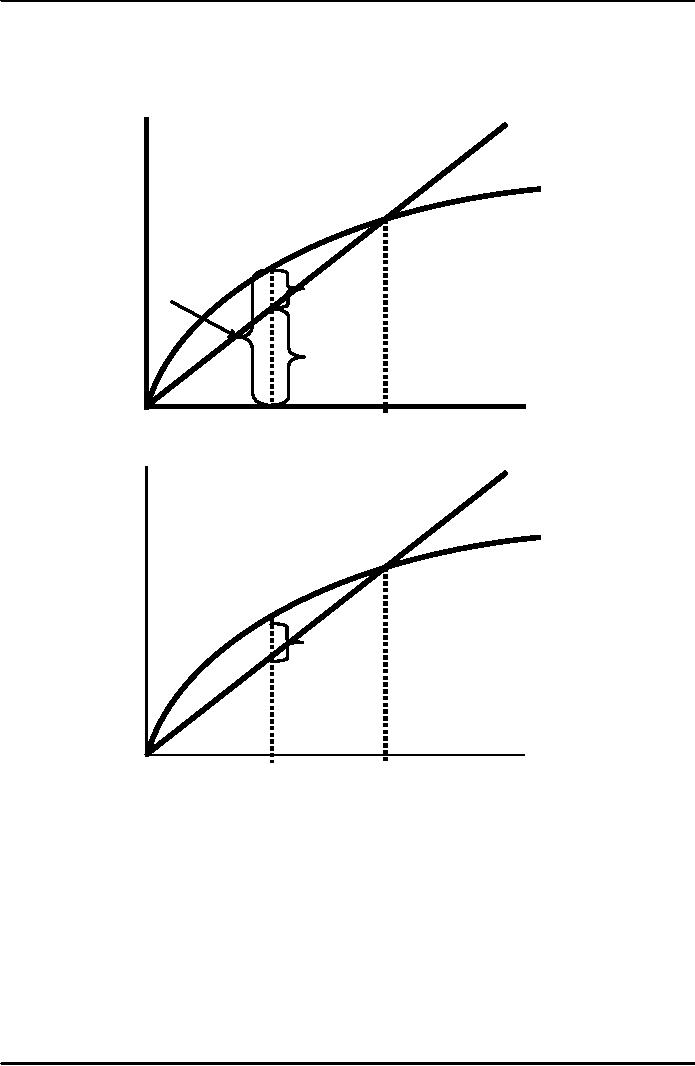
Moving
toward the steady
state
Investment
and
δk
depreciation
Δk
=
sf(k)
-
δk
sf(k)
Δk
Investment
depreciation
k1
k*
Capital
per
worker,
k
δk
Investment
and
depreciation
sf(k)
Δk
k1
k*
Capital
per
worker,
k
75
Macroeconomics
ECO 403
VU
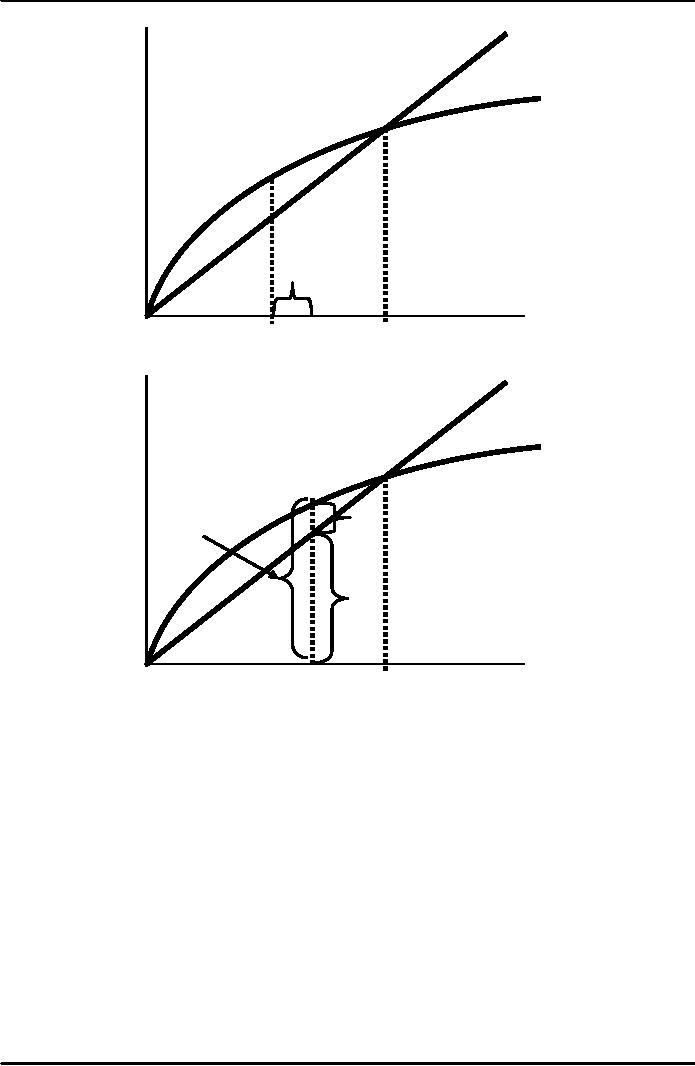
δk
Investment
and
depreciation
sf(k)
Δk
k1
k2
k*
Capital
per
worker,
k
δk
Investment
and
depreciation
sf(k)
Δk
investment
depreciation
k2
k*
Capital
per
worker,
k
76
Macroeconomics
ECO 403
VU
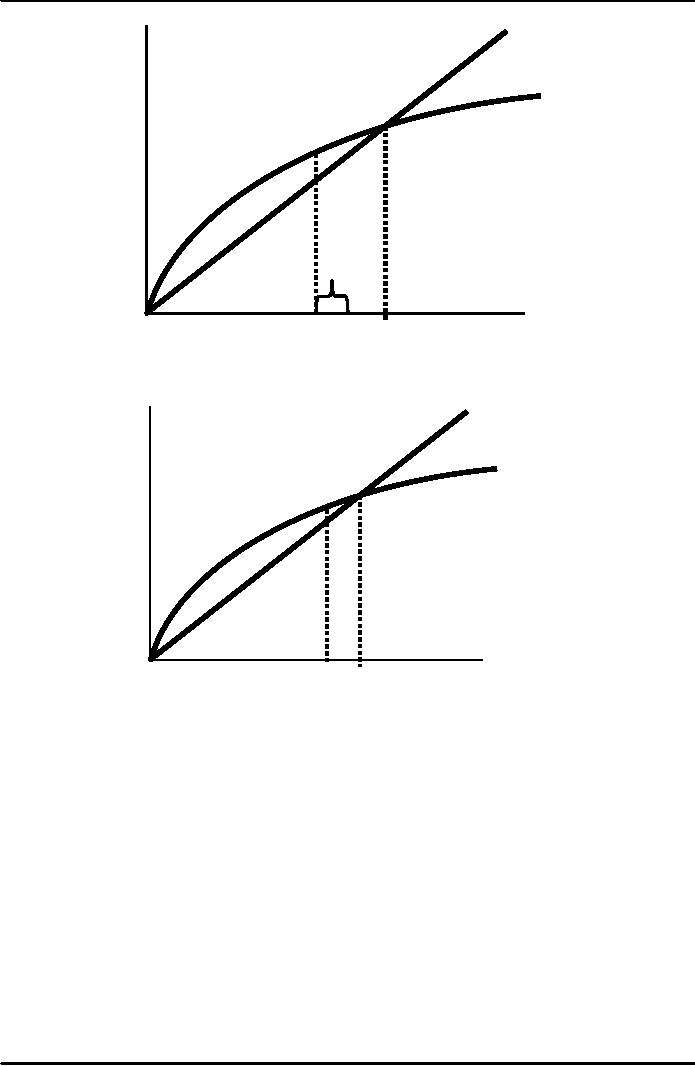
δk
Investment
and
depreciation
sf(k)
Δk
k3
k2
k*
Capital
per
worker,
k
δk
Investment
and
depreciation
sf(k)
As
long as k
<
k*, investment
will
exceed
depreciation,
and
k will
continue to grow
toward
k*.
k3 k*
Capital
per
worker,
k
Now
you try:
Draw
the Solow model diagram,
labeling the steady state
k*.
�
On
the horizontal axis, pick a
value greater than k*
for
the economy's initial
capital
�
stock.
Label it k1.
Show
what happens to k
over
time.
�
Does
k
move
toward the steady state or
away from it?
�
77
Macroeconomics
ECO 403
VU
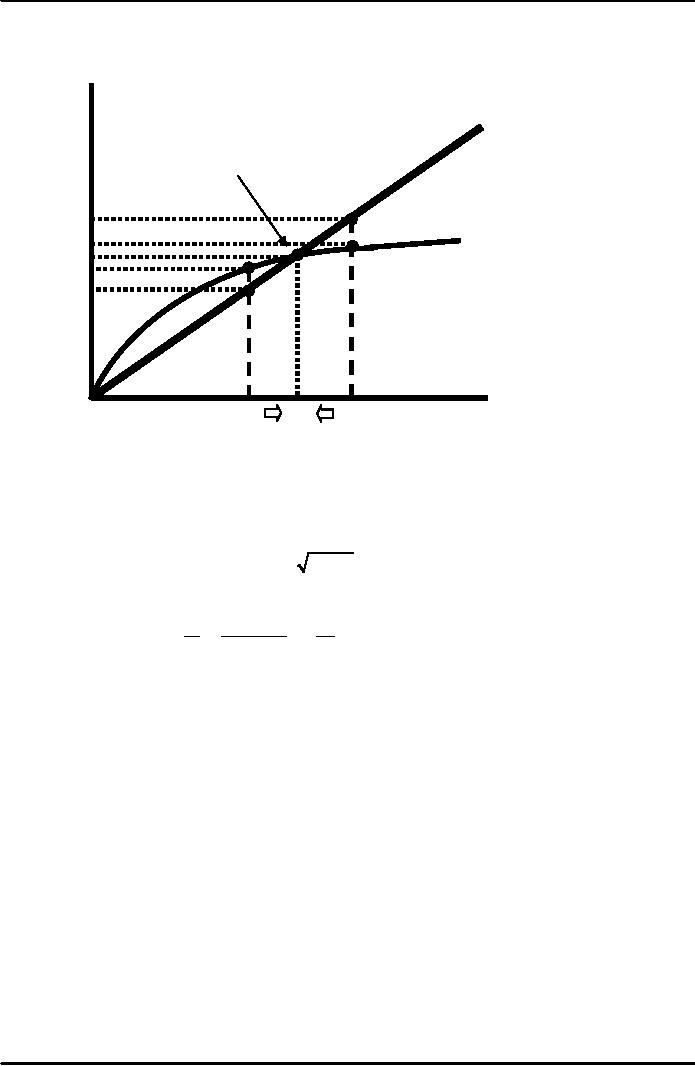
The
Steady State
Investment
and
Depreciation
Depreciation,
k
At
k*, investment equals
depreciation and capital
will
not
change over time.
Investment,
s f(k)
i*
= δk*
k*
k1
k2
Capital
per
worker, k
A
numerical example
Production
function (aggregate):
Y
= F
(K
, L
) =
K
� L
= K
1 / 2L1 / 2
To
derive the per-worker
production function, divide
through by L:
1/2
Y
K 1 / 2L1 / 2 ⎛
K
⎞
=
=⎜
⎟
L
L
⎝L
⎠
Then
substitute y
=
Y/L
and
k
=
K/L
to
get
y
= f
(k
) =
k
1 /
2
Assume:
�
s
=
0.3
�
δ
=
0.1
�
initial value of
k
=
4.0
78
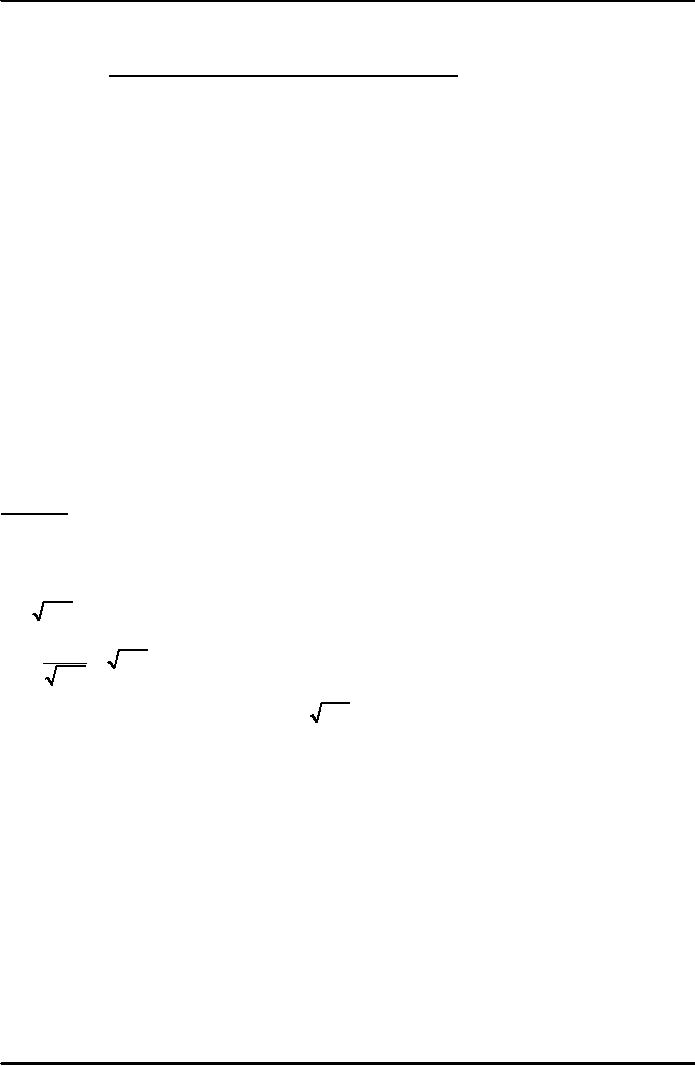
Macroeconomics
ECO 403
VU
Approaching
the Steady State
δk
Δk
Year
k
y
c
i
1
4.000
2.000
1.400
0.600
0.400
0.200
2
4.200
2.049
1.435
0.615
0.420
0.195
3
4.395
2.096
1.467
0.629
0.440
0.189
4
4.584
2.141
1.499
0.642
0.458
0.184
...
10
5.602
2.367
1.657 0.710 0.560
0.150
...
25
7.351
2.706
1.894 0.812 0.732
0.080
...
100
8.962
2.994
2.096 0.898 0.896
0.002
...
∞
9.000
3.000
2.100 0.900
0.900
0.000
Exercise:
solve for the steady
state
Continue
to assume
s
= 0.3,
δ
=
0.1, and y
=
k
1/2
Use
the equation of
motion
Δk
=
s
f(k) -
δk
to
solve for the steady-state
values of k,
y, and
c.
Solution:
Δk
= 0
def.
of steady state
s
f (k
*) =
δ k *
eq'n
of motion with Δk
= 0
0.3
k
* =
0.1k
*
using
assumed values
k*
=
k*
3=
k*
Solve
to get: k
* =
9
and
y
* =
k * =
3
Finally,
c
* =
(1
-
s )y
* =
0.7
�
3
=
2.1
79
Macroeconomics
ECO 403
VU
An
increase in the saving
rate
δk
Investment
and
depreciation
s2 f(k)
s1 f(k)
k
K1
*
K2
*
An
increase in the saving rate
raises investment causing
the capital stock to grow
toward a
new
steady state
Prediction:
Higher
s
⇒ higher
k*.
�
And
since y
=
f(k)
,
�
higher
k*
⇒ higher
y*
.
Thus,
the Solow model predicts
that countries with higher
rates of saving and
�
investment
will have higher levels of
capital and income per worker in
the long run.
80
Macroeconomics
ECO 403
VU
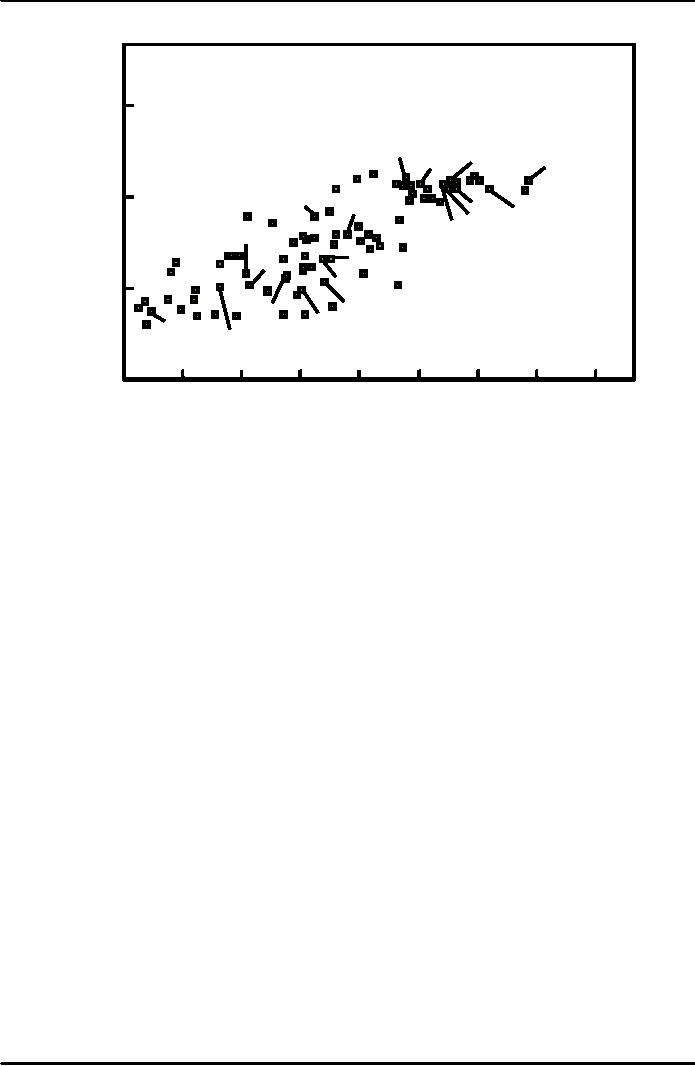
International
Evidence on Investment Rates
and Income per
Person
Income
per
person
in 1992
(logarithmic
scale)
100,000
Canada
Denmark
Germany
Japan
U.S.
Finland
10,000
Mexico
U.K.
Brazil
Singapore
Italy
France
Pakistan
Egypt
Ivory
Peru
Coast
Indonesia
1,000
Zimbabwe
India
Kenya
Uganda
Chad
Cameroon
100
25
30
35
0
5
10
40
15
20
Investment
as percentage of output
(average
19601992)
81
Table of Contents:
- INTRODUCTION:COURSE DESCRIPTION, TEN PRINCIPLES OF ECONOMICS
- PRINCIPLE OF MACROECONOMICS:People Face Tradeoffs
- IMPORTANCE OF MACROECONOMICS:Interest rates and rental payments
- THE DATA OF MACROECONOMICS:Rules for computing GDP
- THE DATA OF MACROECONOMICS (Continued…):Components of Expenditures
- THE DATA OF MACROECONOMICS (Continued…):How to construct the CPI
- NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES
- NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES (Continued…)
- NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES (Continued…)
- NATIONAL INCOME: WHERE IT COMES FROM AND WHERE IT GOES (Continued…)
- MONEY AND INFLATION:The Quantity Equation, Inflation and interest rates
- MONEY AND INFLATION (Continued…):Money demand and the nominal interest rate
- MONEY AND INFLATION (Continued…):Costs of expected inflation:
- MONEY AND INFLATION (Continued…):The Classical Dichotomy
- OPEN ECONOMY:Three experiments, The nominal exchange rate
- OPEN ECONOMY (Continued…):The Determinants of the Nominal Exchange Rate
- OPEN ECONOMY (Continued…):A first model of the natural rate
- ISSUES IN UNEMPLOYMENT:Public Policy and Job Search
- ECONOMIC GROWTH:THE SOLOW MODEL, Saving and investment
- ECONOMIC GROWTH (Continued…):The Steady State
- ECONOMIC GROWTH (Continued…):The Golden Rule Capital Stock
- ECONOMIC GROWTH (Continued…):The Golden Rule, Policies to promote growth
- ECONOMIC GROWTH (Continued…):Possible problems with industrial policy
- AGGREGATE DEMAND AND AGGREGATE SUPPLY:When prices are sticky
- AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…):
- AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…):
- AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…)
- AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…)
- AGGREGATE DEMAND AND AGGREGATE SUPPLY (Continued…)
- AGGREGATE DEMAND IN THE OPEN ECONOMY:Lessons about fiscal policy
- AGGREGATE DEMAND IN THE OPEN ECONOMY(Continued…):Fixed exchange rates
- AGGREGATE DEMAND IN THE OPEN ECONOMY (Continued…):Why income might not rise
- AGGREGATE SUPPLY:The sticky-price model
- AGGREGATE SUPPLY (Continued…):Deriving the Phillips Curve from SRAS
- GOVERNMENT DEBT:Permanent Debt, Floating Debt, Unfunded Debts
- GOVERNMENT DEBT (Continued…):Starting with too little capital,
- CONSUMPTION:Secular Stagnation and Simon Kuznets
- CONSUMPTION (Continued…):Consumer Preferences, Constraints on Borrowings
- CONSUMPTION (Continued…):The Life-cycle Consumption Function
- INVESTMENT:The Rental Price of Capital, The Cost of Capital
- INVESTMENT (Continued…):The Determinants of Investment
- INVESTMENT (Continued…):Financing Constraints, Residential Investment
- INVESTMENT (Continued…):Inventories and the Real Interest Rate
- MONEY:Money Supply, Fractional Reserve Banking,
- MONEY (Continued…):Three Instruments of Money Supply, Money Demand