PERT / CPM:Expected length of a critical path, Expected time and Critical path

<< PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack

PERT / CPM:Expected time and Critical path >>

Operations Research (MTH601)

Expected length of a critical path:

The expected length of a sequence of independent activities is simply the sum of their separate expected

lengths. This gives us the expected length of the entire project. We have to calculate the expected length te of every

activity with the weights attached to the three time estimates and find the critical path in the manner described

previously. The expected length of the entire project denoted by Te is the length of the critical path (i.e.) the sum of

the, te's of all activities along the critical path.

In the same way, the variance of a sum of independent activity times is equal to the sum of their individual

variances. Since Te is the is the sum of te's along the critical path, then variance of Te equals the sum of all the

variances of the critical activities. The standard deviation of the expected project duration is the square root of the of

the variance Te as calculated above.

At this juncture, consider the following example to illustrate the application of these formulae.

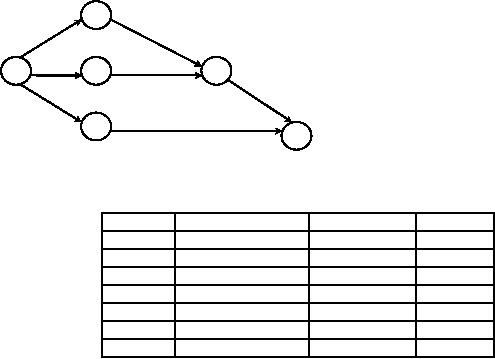
Example

1,1,7

1,1,1

1,4,7

2,5,14

3,6,15

2,2,8

2,5,8

Fig. 20

Activity

Expected time (te)

Std. deviation

Variance

1-2

(1+4+7)/6 = 2

(7-1)/6 = 1

1-3

(1+16+7)/6 = 4

(7-1)/6 = 1

1-4

(2+8+8)/6 = 3

(8-2)/6 = 1

2-5

(1+4+1)/6 = 1

(1-1)/6 = 0

3-5

(2+20+14)/6 = 6

(14-2)/6 = 2

4-6

(2+20+8)/6 = 5

(8-2)/6 = 1

5-6

(3+24+15)/6 = 7

(15-3)/6 = 2

For each activity, the optimistic mostly likely and pessimistic time estimates are labeled in the same order.

Using PERT formulae for te and St tabulate the results as above.

To calculate the critical path, list all the three paths with their expected time of completion from figure 21.

1-2-5-6

= 10

Operations Research (MTH601)

1-3-5-6 = 17

1-4-6

Table of Contents: