PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH

<< PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK

PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack >>

Operations Research (MTH601)

The project of budgeting can be displayed in a network or project graph by an arrow diagram. Jobs are

shown as arrows leading from one node to the other as in Figure 2.

Fig. 2

From the arrow diagram 2, we infer that activity A is the first job. Jobs B and C start only after A is over. A is called

the predecessor of B and C and B and C the successors of A.

RULES FOR CONSTRUCTION OF NETWORK

(a)

Each activity is represented by one and only one arrow. This means that no single activity can be

represented twice in a network.

(b)

No two activities can be identified by the same end events. This means that there should not be

loops in the network.

(c)

Time follows from left to right. All the arrows point in one direction. Arrows pointing in opposite

direction must be avoided.

(d)

Arrows should not cross each other.

(e)

Every node must have at least one activity preceding it and at least one activity following it,

except for the nodes at the very beginning and at the very end of the network.

DUMMY ACTIVITIES

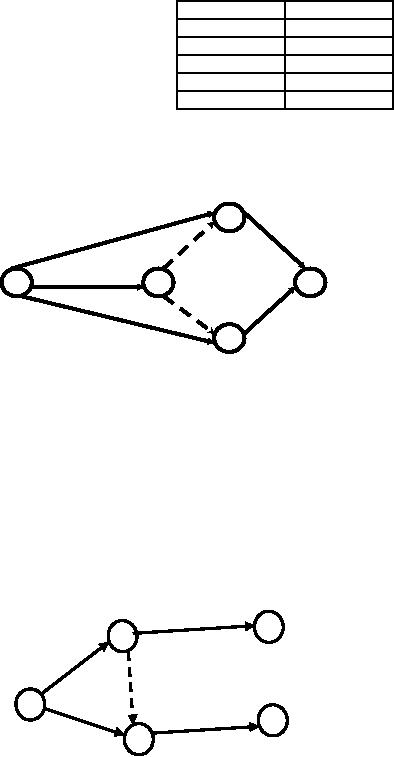
There is a need for dummy activities when the project contains groups of two or more jobs which have

common predecessors. The time taken for the dummy activities is zero.

Suppose we have the following project of jobs with their immediate predecessors.

Jobs

Immediate

Operations Research (MTH601)

predecessors

A, B

B, C

Activity B is the common immediate predecessor of both D and E. A is the immediate predecessor of D

alone and C is the predecessor of E. Let B lead into two dummy jobs D1 and D2 and let D1 be an immediate

predecessor of D and D2 of E as shown in Figure 3.

Fig. 3

Dummy arrow represents an activity with zero time duration. It is represented by a dotted line and is

introduced in a network to clarify activity pattern under the following situations.

(i) It is created to make activities with common starting and finishing events distinguishable.

(ii) To identify and maintain the proper precedence relationship between activities those are not connected

by events.

Consider an example where A and B are parallel (concurrent activities). C is dependent on A and D is

dependent on both A and B. Such a situation can be represented easily by use of dummy activity as shown in Figure

Fig. 4

Operations Research (MTH601)

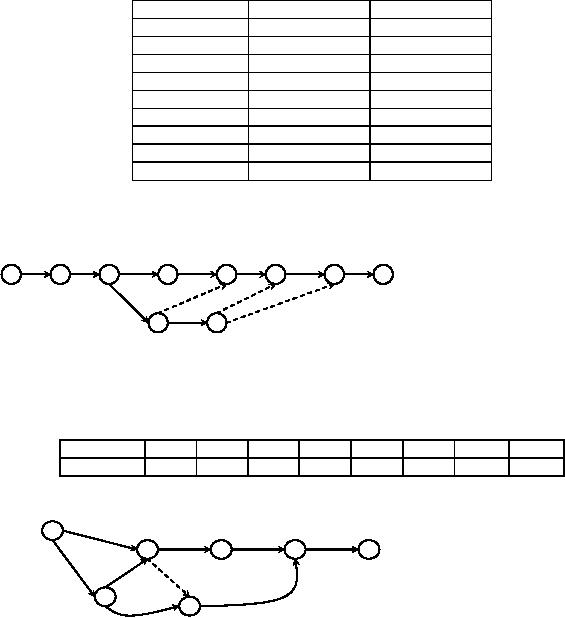
Example 2: A project consists of the following activities whose precedence relationship is given below. Draw an

arrow diagram to represent the project.

Activity

Followed by

Preceded by

B, C

C, A

E, B

G, F

E, D

H, I

G, F

G, H

Solution

Fig. 5

Example Consider the following project. Draw an arrow diagram to represent the project.

Activity

Precedence

B, C

B,C,D

H,G

Solution:

Fig. 6

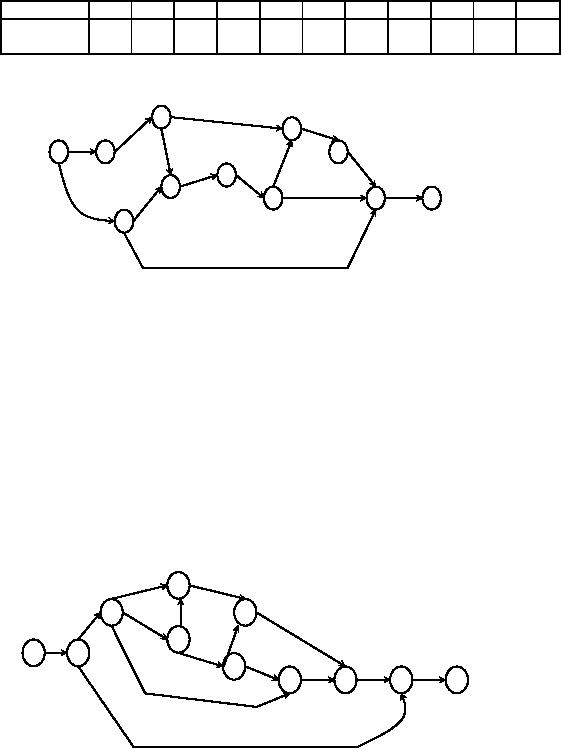
Example Consider the project of building a house. The details of the project activities are tabulated below. Draw

network.

Operations Research (MTH601)

Activity

Immediate

Predecessor

B,C

G,H

E,I,J

Solution:

6 G

Fig. 7

Example A project has the following activities. The relationships among the activities are given below. Construct

the network.

A is the first operation.

B and C can be performed parallel and are immediate successors to A.

D,E and F follow B.

G follows E.

H follows D, but it cannot start till E is complete.

I and J succeed G.

F and J precede K.

H and I precede L.

M succeeds L and K.

The last operation N succeeds M and C.

Solution:

Fig. 8

Example

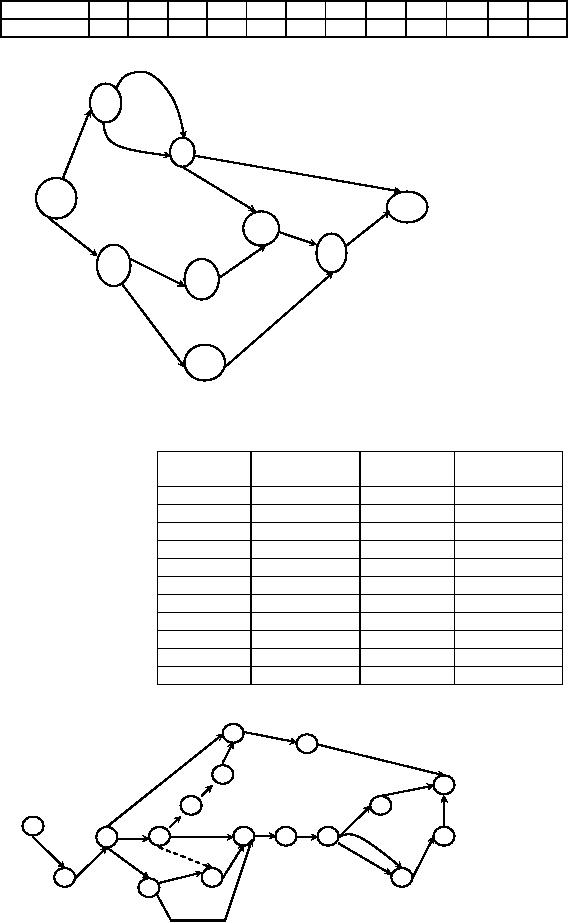
Operations Research (MTH601)

Activity

Predecessor -

C,D E

C,D

G,H

J,K

Fig. 9

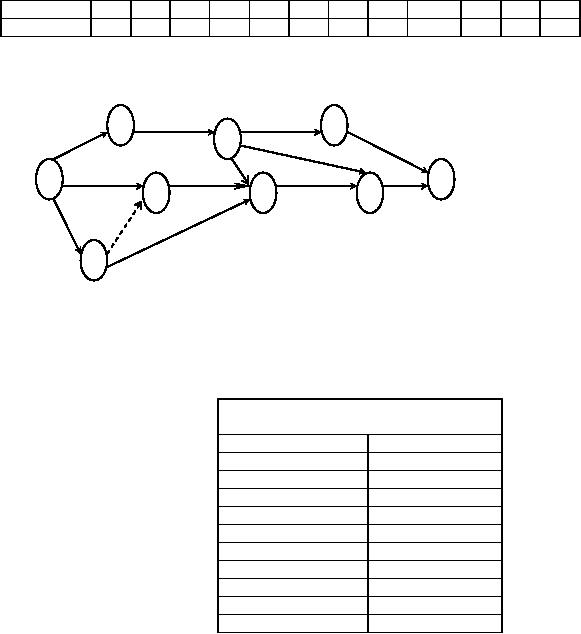
Example Draw network from the following list of activities.

Job

Immediate

Job

Immediate

Name

predecessor

Name

predecessor

l, m

c, f

g, h, i

p, q

Operations Research (MTH601)

Fig. 10

Example For a project of 12 activities the details are given below. Draw PERT network.

Activity

Dependence

B,C

D,F,H

I,J

Solution:

Fig. 11

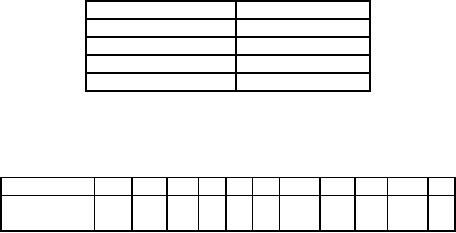
Exercises

(a) Explain in brief PERT, CPM and dummy activities with reference to Project Management.

(b) The following information is known for a project. Draw the network and find the critical path.

Capital letters denote activities and the numbers in bracket denote activities' time.

This must be

before

This can

completed

start

A(30)

B(7)

C(10)

D(14)

E(10)

F(7)

Operations Research (MTH601)

G(21)

H(7)

J(15)

I(12)

K(30)

L(15)

Draw network diagram for the following activities whose predecessors are given in the table below.

Job

Immediate

Predecessors

D,F

G,I

TO FIND THE CRITICAL PATH

After listing all the activities with their precedence relationship we project these activities in a project graph

represented by arrows or Activity On Node diagram (AON). Now we have to find the minimum time required for

completion of the entire project. For this we must find the longest path with the sequence of connected activities

through the network. This is called the critical path of the network and its length determines the time for completion

of the project. The activities in the critical path are so critical that, if they are delayed, the project completion date

cannot be met and the project finish time will have to be extended. We shall now see how to identify the critical

path, the critical activities and the duration of the project. The meaning of path and length of a path should first be

made clear. Let us take following example.

Operations Research (MTH601)

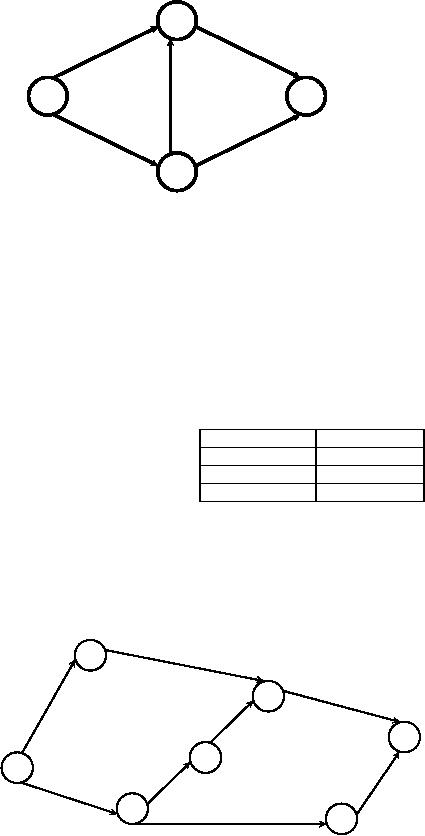
Consider the following network shown in figure 12.

Fig. 12

We have five activities A, B, C, D and E with the time of completion of the activities 5, 6, 7, 3 and 6 days

respectively. We represent the activities in a network shown in the same figure.

In this network, there are three ways to get from the starting point at node 1 and travel through the network

to end at node 4. These ways are called paths. Thus, a path is defined as "a set of nodes connected by lines which

begin at the initial node of a network and end at the terminal node". In figure12, there are three paths namely, 1-3-4,

1-2-3-4 and 1-2-4 where the numbers represent the nodes. The length of a path in a network is the total time it takes

to travel along the path. This time is calculated by adding the individual times between the connected nodes on the

path. A path is called a critical path if it is the longest the path in a project network. We have the times of the three

distinct paths has shown below.

Path

Time (days)

1-3-4

5 + 3 = 8 days

1-2-3-4

6 + 7 + 3 = 16

1-2-4

6 + 6 = 12

The path connecting the nodes 1,2,3 and 4 constitutes the longest path and hence 1-2-3-4 is the critical path.

The minimum time to complete the project is the time taken for the longest path namely 16 days. The activities B (1-

2), C (2-3) and D(3-4) constitute the critical activities. These jobs are critical in determining the project's duration.

The critical path for the above example can be shown in the diagram.

The same can be calculated using Activity On Node diagram. The AON diagram is as shown in figure 13.

A,5

D,3

End

C,7

Table of Contents: