 |
Operations
Research (MTH601)
250
EXERCISES
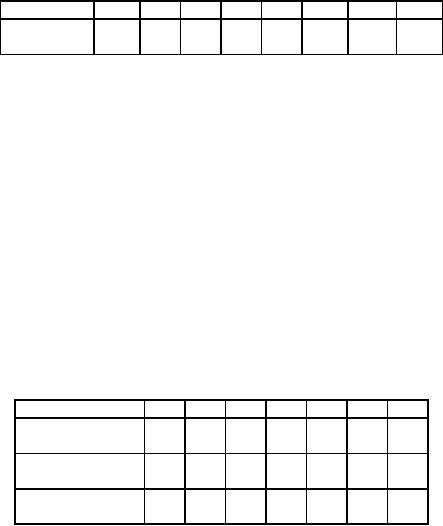
1.
The
cost of a machine is Rs.
6100 and its scrap value is
only Rs. 100/-. The
maintenance costs are
found
from experience to
be.
Year
1
2
3
4
5
6
7
8
Maintenance
100
250
400
600
900
1250
1600
2000
cost
(Rs.)
When
should the machine be
replaced?
2.
A
machine costs Rs. 8000.
Annual operating costs are
Rs. 1000 for the
first year, and then
increase by
Rs.
500 every year. Resale
prices are Rs. 4000
for the first year
and then decrease by Rs.
500 every
year.
Determine at which age it is profitable
to replace the
machine.
3.
A
machine owner finds from his
past experience that the
maintenance costs are Rs.
200 for the
first
year
and then increase by Rs.
200 every year. The
costs of the machine type A
Rs. 9000. Determine
the
best
age at which to replace the
machine. If the optimum
replacement is followed what will be
the
average
yearly cost of owning and
operating the machine? Machine
type B costs Rs. 10000/-.
Annual
operating
costs are Rs. 400
for the first year
and then increase by Rs.
800/- every year. The
machine
owner
has now the machine
type A, which is one year
old. Should it be replaced with B
type and if so,
when?
4.
Explain
briefly the difference in
replacement policies of items, which
deteriorate gradually and
items,
which
fail completely. A machine shop
has a press, which is to be
replaced as it wears out. A new
press
is
to be installed now. Further an
optimum replacement plan is to be
found for next 7 years after
which
the
press is no longer required.
The following data is given
below.
Year
1
2
3
4
5
6
7
Cost
of
200
210
220
240
260
290
320
installation
(Rs.)
Salvage
value
100
30
30
20
15
10
0
(Rs.)
Operating
cost
60
80
100
120
150
180
230
(Rs.)
Find
an optimum replacement policy
and the corresponding
minimum cost.
ITEMS
DETERIORATING WITH TIME VALUE OF
MONEY
In
the previous section we did
not take the interest
for the money invested,
the running costs and
resale
value.
If the effect of time value
of money is to be taken into
account, the analysis must
be based on an
equivalent
cost. This is done with
the present value or present
worth analysis.
For
example, suppose the
interest rate is given as
10% and Rs. 100
today would amount to Rs.
110
after
a year's time. In other words the
expenditure of Rs. 110 in
year's time is equivalent to
Rs. 100 today.
Likewise
one rupee a year from
now is equivalent to
(1.1)-1 rupees today and
one-rupee in 'n'
years from now is
equivalent
to (1.1)-n rupees today. This
quantity (1.1)-n
is called
the present value or present
worth of one rupee
spent
'n' years from
now.
250
Operations
Research (MTH601)
251
We
can establish an algebraic formula
for the present worth
value.
Let
M
=
purchase price of an item.
Rn =
running cost in year
n.
r
=
rate of interest
The
present worth of a rupee to be
spent after a year is
denoted by v
and
given by
v
=
1/(1 + r)
v
is
called the discount rate.
Let the item be replace
after n
years,
and that the expenditure
can be considered to
take
place at the beginning of
each year. Then the
present worth of expenditure
denoted by
P(n)
= M + R1 +
vR2 + v2R3
+ ... +
vn-1Rn
We
note that P(n)
increases as n
increases.
The
present worth of expenditure
incurred for n
years
including the capital cost is
obtained from a
money
lending institution and we repay
the loan by fixed annual
installments throughout the
life of the machine.
The
present worth of this fixed
annual installment x
for
n
years
is
=
x
+ vx + v2x
+
... + vn-1x
=
x
(1
+ v
+ v2 + ... + vn-1)
n
1-
v
P(n)
=
x
(using
the formula for a geometric
series)
1-
v
Since
this is the sum repaid, we
equate the present worth of
expenditure to the present
worth or repayment.
Then,
1-
v
x=
P(n).
n
1-
v
So,
the best period at which to
replace the machine is the
period n
which
minimizes x.
Since (1 - v)
is
constant,
it is enough if we minimize P(n)/(1
- vn).
The best period at which to
replace the machine is the
period
n
which
minimizes P(n)
/ (1 - vn) =
F(n)
(say).
The
value of n
is
not continuous but discrete
and hence we are not in a
position to employ
differentiation
to find the optimum
period.
We
can assume n
=
1,2,3 etc., find P(n)
for different years and
calculate using the formula
for x
above.
Choose
n which minimize x.
We shall illustrate this idea with an
example.
Example
The
initial cost of an item is
Rs. 15000 and maintenance or
running cost for different
years is given
below.
Year
1
2
3
4
5
6
7
Running
2500
3000
4000
5000
6500
8000
10000
cost
Rs.
251
Operations
Research (MTH601)
252
What
is the replacement policy to be
adopted if the capital is
worth 10% and no salvage
value.
We
know that
Solution
P(n)
= M
+
R1 + vR2 + ... + vn-1Rn
Use
this equation for n = 1, 2, 3,
...
M
=
Rs. 15000
1
v=
=
0.909
1
+
0.1
R1 to R7 are as given in the
problem. The best time to
replace the item is
n
which
is governed by x
=
P(n)
(1 - v)
/ (1 - vn).
We
use a tabular method to
present the details for
analysis in table 6.
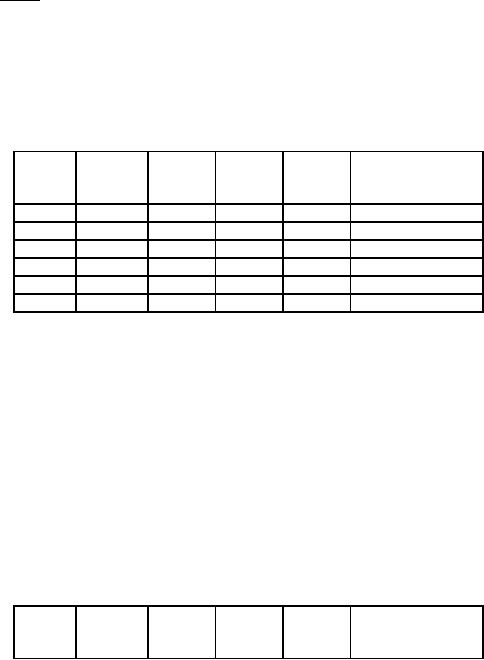
Table
6
n-1
vn-1 Rn
P(n)
(1-v)/(1-vn)
Year
n
Running
P(n)
v
cost,
(PWF)
Rn(Rs.)
1
2500
1.000
2500
17500
17500
2
3000
0.909
2727
20227
10595
3
4000
0.826
3304
23531
8602
4
5000
0.751
3755
27286
7826
5
6500
0.683
4440
31726
7609
6
8000
0.621
4968
36694
7660
We
see from table 6 the
value of the fixed annual
installment given by the last column is
minimum at
year
5. So it is optimal to replace the
machine after fiver
years.
A
manufacturer is offered two
machines A
and
B.
A is priced at Rs. 10000 and
running costs
Example
are
Rs. 1600 for each of
the first five years,
increasing by Rs. 400 per
year in the sixth and
subsequent years.
Machine
B
which
has the same capacity as
A,
costs Rs. 5000 but
will have running costs of
Rs. 2400 per year
for
six
years increasing by Rs. 400
per year, there after. If
the capital is worth 10%
per year which machine
should
be
purchased?
We
prepare two tables 7 and 8
for machine A
and
for machine B
respectively
as shown.
Solution
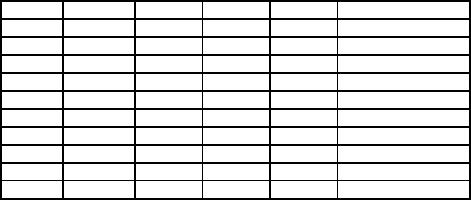
Table
7
Machine
A
vn-1
vn-1 Rn
P(n)
(1-v)/(1-vn)
Year
n
Running
P(n)
cost,
(PWF)
Rn(Rs.)
252
Operations
Research (MTH601)
253
1
1600
1.000
1600
11600
11600
2
1600
0.909
1454
13054
6835
3
1600
0.8264
1322
14376
5254
4
1600
0.7513
1202
15578
4467
5
1600
0.6830
1092
16670
3997
6
2000
0.6209
1242
17912
3739
7
2400
0.5645
1354
19266
3598
8
2800
0.5132
1436
20702
3527
9
3200
0.4665
1492
22194
3503
10
3600
0.4241
1526
23720
3508
11
4000
0.3854
1542
25262
-
253

Operations
Research (MTH601)
254
Table
8
Machine
B
vn-1
vn-1 Rn
P(n)
(1-v)/(1-vn)
P(n)
Year
n
Running
(PWF)
cost,
Rn(Rs.)
1
2400
1.000
2400
7400
7400
2
2400
0.9091
2182
9582
5017
3
2400
0.8264
1983
11565
4227
4
2400
0.7513
1802
13368
3833
5
2400
0.6830
1639
15007
3598
6
2400
0.6209
1490
16497
3443
7
2800
0.5645
1581
18078
3376
8
3200
0.5132
1642
19720
3360
9
3600
0.4665
1679
21399
3378
10
4000
0.4241
1696
23095
3378
11
4400
0.3854
1696
24791
-
From
the above tables 7 and 8 we
find that machine A is
replaced at the end of 9th
year with fixed
annual
payment of Rs. 5503 and
that the machine B is
replaced at the end of 8
years and the fixed
annual
payment
is Rs. 3360. Comparing the
two figures, machine B is to be
purchased.
EXERCISES
1.
A
person is considering purchasing a
machine for his own factory.
Relevant data about
alternative
machines
are as follows.
Machine
A
Machine
B
Machine
C
Present
investment
Rs.
10000
12000
15000
Total
Annual cost
Rs.
2000
1500
1200
Life
(years)
10
10
10
Salvage
value
Rs.
500
1000
1200
As
an adviser to the buyer, you
have been asked to select
the best machine,
considering 12%
normal
rate
of return. You are given
that:
(a)
Single payment present worth
factor (PWF) at 12 % rate for 10
years = 0.322.
(b)
Annual series present worth
factor (PWFs) at 12 % rate
for 10 years = 5.650.
2.
Discuss
the optimum replacement
policy for items when
maintenance cost increases
with time and
the
money
value changes with constant
rate. If you wish to have a
return of 0 percent per
constant rate. If
you
wish to have a return of 10
percent per annum for
investment, which of the
following plan you
prefer?
Plan
A
Plan
B
First
Cost (Rs.)
200000
250000
Scrap
value for 15 year
(Rs.)
150000
180000
254

Operations
Research (MTH601)
255
Excess
of annual revenue over
annual
disbursement
(Rs.)
25000
30000
ITEMS
THAT FAIL COMPLETELY AND
SUDDENLY
There
is another type of problem
where we consider the items
that fail completely. The
item fails such
that
the loss is sudden and
complete. Common examples are
the electric bulbs,
transistors and replacement
of
items,
which follow sudden failure
mechanism.
Strategy
(1) (IR)
Under
this strategy equipments or facilities
break down at various times.
Each breakdown can be
remedied
as it occurs by replacement or repair of
the faulty unit.
Examples:
Vacuum tubes,
transistors.
Strategy
(2) (IPR)
According
to this strategy, before any
unit fails, either each
unit is replaced or preventive
maintenance
is
performed on it as per the
following rules.
(a)
Determine
the optimum life I of each
item. Replace all those
items, which have given
the optimum life
though
they still survive.
(b)
Replace
an item if it fails before
the optimum life T.
Examples:
Car tyres, aircraft
engines.
Strategy
(3) (CPR) or Group
replacement
As
per this strategy, an optimal
group replacement period
'P'
is determined and common
preventive
replacement
is carried out as
follows.
(a)
Replacement
an item if it fails before
the optimum period
'P'.
(b)
Replace
all the items every
optimum period of 'P'
irrespective of the life of
individual item.
Examples:
Bulbs, Tubes, and
Switches.
Among
the three strategies that
may be adopted, the third
one namely the group
replacement policy
turns
out to be economical if items
are supplied cheap when
purchased in bulk quantities.
With this policy,
all
items
are replaced at certain
fixed intervals. The optimum
interval can be worked out as illustrated
in the
example
to follow.
The
following mortality rates
have been observed for a
certain electric
bulb.
Example
Week
1
2
3
4
5
6
7
8
Percentage
failure
by
end of week
5
13
25
43
68
88
96
100
There
are 1000 bulbs in a factory
and it costs Rs. 400 to
replace and individual bulb,
which has burnt
out.
If all bulbs were replaced
simultaneously, it would cost
Re. 1 per bulb. It is
proposed to replace all
bulbs at
255

Operations
Research (MTH601)
256
fixed
intervals, whether or not
they have burnt out,
and to continue replacing
burnt out bulbs as they
fail. At
what
intervals should all the
bulbs be replaced?
We
make two assumptions in solving
the problem.
Solution:
(1)
The bulbs that fail
during a week are replaced
before the end of the
week.
(2)
The actual probability of failures
during a week for a subpopulation of
the bulbs with the
same age
is
the same as the probability of failure
during the week for that
sub-population.
Let
Pi be
the probability that a bulb newly
installed fails during the
ith
week of its life. This can be
obtained
from mortality table shown
below in table 9.
Table
9
End
of the week
1
2
3
4
5
6
7
8
Probability
of
failure
during
0.05
0.08
0.12
0.18
0.25
0.20
0.08
0.04
the
ith
week
Now,
we calculate the number of
bulbs that fail during a
particular week and require
replacement.
Let
ni be
the number of replacement
made at the end of the
ith
week if all 1000 bulbs were
new initially
with
the assumptions made above.
We obtain,
n0 = n0
=
1000
n1 = n0p1
=
50
n2 = n0p2 + n1p1 = 80 + 3
=
83
n3 = n0p3 + n1p2 + n2p1 = 120 + 4 + 4
=
128
n4 = n0p4 + n1p3 + n2p2 + n3p1 = 180 + 6 + 7 + 6
=
199
n5 = n0p5 + n1p4 + n2p2 + n3p2 + n4p1 = 250+9+10+10+10
=
289
If
the policy is to replace all
the bulbs simultaneously
every week the cost of installation of
1000 bulbs
at
the rate of Re. 1 per
bulb is rate of Rs. 4 per
bulb. Then the cost of
replaced bulbs = Rs. 200.
Total cost per
week
= Rs. 1200.
If
all the bulbs were
replaced at the end of two
weeks, the cost of new bulbs
for group replacement
is
Rs.
1000 and the number of
bulbs to be replaced during
first two weeks would be
133 and the cost
for the same
is
133 x
4
=Rs. 532. Total cost
would be Rs. 1532. This
expenditure is spread over a
period of two weeks.
Hence
the
average cost per week
would be Rs. 766, which is
less than that if the
policy is to replace the
bulbs every
week.
Extending
the same logic, if the
policy would be to replace
all bulbs once in three
weeks, the cost
would
be Rs. 1000 + 261 x 4 = Rs.
2044. Hence the average
cost per week would be Rs.
681. We try for
the
time
period of four weeks and the
cost would be Rs. 1000 +
1044 + 796 = Rs. 2840.
Thus we see that
the
256
Operations
Research (MTH601)
257
average
cost per week is Rs. 710
which is more than that
incurred for the policy to
replace the bulbs once
in
three
weeks. Hence the optimum
period of group replacement is
three weeks.
In
the above analysis it was
assumed to adopt the policy
of group replacement and the
fixed interval of
replacement
was three weeks. But we
have to examine the policy
if we replace bulbs as and
when they fail
(without
group replacement). For this
the average life of the bulb
is to be calculated. Multiplying the
probability
can
do this and the
corresponding life of the bulb
for all the possible
cases and add them
up.
Thus
we have the expected life of
a bulb would be (0.05 x 1) + (0.08 x 2) +
(0.12 x 3) + (0.18 x 4) +
(0.25
x 5) + (0.20 x 6) +(0.08 x 7) + (0.04 x
8) = 4.62 weeks. Hence the
number of replacement of bulbs
per
week
would be 1000/4.62 = 216
bulbs which would cost
Rs. 864, at the rate of
Rs. 4 per bulb. This is more
than
what
we had in group replacement
(cost Rs. 681). Hence we
conclude that the group
replacement policy is
better
and
replace all bulbs at
required interval of three
weeks.
EXERCISES
1.
The
following failure rates have
been observed for certain
type of light bulb.
End
of week
1
2
3
4
5
6
7
8
prob.
of failure
to
date
0.05
0.13
0.25
0.43
0.68
0.88
0.96
1.00
There
are 1000 light bulbs in a
factory. The cost of replacing an
individual bulb is Rs. 500.
If the cost of
group
replacement is Rs. 1.20 what is
the best interval between
group replacements?
2.
A
computing machine has a
large number of electronic
tubes, each of which has a
life normally
distributed
with a mean of 1200 hrs.
with a standard deviation of
160 hrs. Assume the
machine is in
operation
for two shifts (2 x 8 = 16 hrs.)
per day. If all the
tubes were to be replaced at
fixed interval, the
cost
is Rs. 30 for a tube.
Replacement of individual tubes,
which fail in service, would
cost Rs. 80 for
labour
and parts plus the
cost of computer downtime, which
runs about Rs. 800
for an average tube
failure.
How frequently all tubes be
replaced?
STAFF
REPLACEMENT PROBLEMS
A
research team is planned to
raise the strength of 50
chemists and then to remain
at that level.
Example
The
number of recruits depends on
their length of service and
is as follows.
Year
1
2
3
4
5
6
7
8
9
10
%
left at the
end
of year
5
36
56
63
68
73
79
87
97
100
What
is the recruitment per year
to maintain the required strength?
There are 8 senior posts
for which
the
length of service is the main criterion.
What is the average length of
service after which a new
entrant
expects
promotion to one of the
posts?
Solution:
Table
10
257
Operations
Research (MTH601)
258
At
the end
Probability
of Probability of Number
of
of
year
leaving
in-service
person
0
0
1.00
100
1
0.05
0.95
95
2
0.36
0.64
64
3
0.56
0.44
44
4
0.63
0.37
37
5
0.68
0.32
32
6
0.73
0.27
27
7
0.79
0.21
21
8
0.87
0.13
13
9
0.97
0.03
3
10
1.00
0.00
-
436
From
the table 10 we find probability of
leaving at the end of year
and also the probability of
inservice
at
the end of year.
If
we select 100 chemists every
year then the total number
of chemists serving in the
team would have
been
436. Hence, to maintain strength of 50
chemists we must
recruit
(100/436)
x 50 = 11.4 = 12 per year
(approx.)
If
pi
is
the probability of a person to be in
service at the end of
ith
year, then out of 12
recruited each
year
the total number of survivals will be 12
x pi.
The chemists in service at
the end of year are
given in the
table
11.
Table
11
No.
of chemists
Year
Probability
of
at
the end of
Survival,
pi
year
= 12 x pi
0
1.00
12
1
0.95
11
2
0.64
8
3
0.44
5
4
0.32
4
5
0.32
4
6
0.27
3
7
0.21
2
8
0.13
2
9
0.03
0
10
0.00
0
If
there are 8 service posts
for which the length of
service is the criterion, then we
see from the table
11
that
there are 3 persons with 6
years experience, 2 with 7
years and 2 with 8 years.
The total number is 7,
which
is
less than 8. Hence the
promotion will be given at the
end of 5 years.
258
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION