 |
Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL |
| << Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL |
| Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION >> |
Operations
Research (MTH601)
227
Arrival
Rate: This is
the rate at which customers
arrive to be serviced. This arrival rate
may not
be
constant. Hence it is treated as a
random variable for which a
certain probability distribution is to be
assumed.
The assumption regarding the
distribution of this value has an
effect upon the mathematical
model. It
is
observed in general that in
queuing theory arrival rate is randomly
distributed according to the
Poisson
distribution.
The mean value of the
arrival rate is denoted by λ
(lambda);
the unit is usually
customers/time
period.
There are queues with
other probability distributions
also.
Service
Rate: This
is the rate at which the
service is offered to the
customers. This can be done by
a
single
server or sometimes by multiple
servers, but this service
rate refers to service
offered by a single
service
channel.
This rate is also a random
variable as the service to
one customer may be different
from the other.
Hence
it is also assumed to follow in
general, the Poisson distribution.
The mean value of the
service rate is μ
(mu);
the unit is customers/time
period. The distribution of this
rate plays a role in the
mathematical model.
Other
distributions are also
assumed.
Infinite
Queue: If
the customers who arrive
and form the queue
are from a large population
(eg.
people
crowding at a cinema theatre, book in
counter etc.) then the
queue is referred to as infinite
queuing
model.
This assumption also has
great influence in the
mathematical formulation and its
solution.
Finite
Queue: If
the customers arrive from a
small number of population
say less than 30,
then this is
treated
as a finite queue. This
value also has an effect in
the mathematical model formulation
and its solution.
Priority:
This
refers to the method of
deciding which customer will
be served next. The
most
common
assumption is first come,
first served (first in,
first out). This assumption
has also an effect in
the
derivation
of formulae used for
analysis.
Expected
Number in Queue: This is
the average or mean number
of customers waiting to be
serviced.
This is denoted by Lq.
Expected
Number in System: This
is the average number of
customers either waiting in
the line
and/or
being serviced, denoted by
L.
Expected
Time in Queue: This is
the expected or mean time a
customer waiting in line
and/or being
serviced,
denoted by Wq.
Expected
Number in Nonempty Queue:
This
is the average or expected
number of customers
waiting
in the line excluding those
times when the queue is
empty. This figure can be arrived by
counting and
averaging
only nonzero values. It
would be equivalent to L.
This expected number in the
nonempty queue is
denoted
by Ln.
Expected
Waiting Time For Nonempty
Queue: This
is the expected time a
customer waits in line
if
he
has to wait at all. This
value is the average of
waiting times for all
customers entering the queue
when the
serving
counter is filled. Customers
entering the channel is
empty needing not have to
wait (zero waiting
time)
and
these values are not
taken into account in arriving at the
average. Wn denotes this
value.
System
Utilization or Traffic Intensity:
This
is the ratio between arrival and
service rate denoted
by
ρ
given
by ( λ
/
μ
).
SINGLE-CHANNEL
INFINITE-POPULATION MODEL
We
assume in queueing theory
that the arrivals or
services be random and
independent of all
other
conditions.
This will lead to the
condition that the distribution of arrival
rate can be shown to be
Poisson. The
227
Operations
Research (MTH601)
228
mean
is independent of time and
not affected by a number of
customers in waiting line, previously
serviced
etc.
This means that the probability of an
arrival during any time
period Δt is
constant an equal to λΔt .
Similarly
we have the conditional probability of a
service executed is also
given as λΔt given
that there is a
customer
to be serviced. We will assume
that the time period
Δt is
so small that higher orders
of Δt ,
are
neglected.
Let
n
be
the number of units in the
system and Pn(t)
be the probability of n
units
in the system at time
t.
The
derivation of expressions is done in
three steps.
Step
1: Find
Pn(t)
in terms of λ
and
μ
.
Step
2: Using
this expression find the
expected number of units in
the system in terms of λ
and
μ
.
Step
3: Using
the results of the previous
step, derive the expressions
for system time
etc.
The
probability of n
units
in the system can be found
by adding the probabilities of all
the ways this
event
could occur. Let us take all
the cases ending up with
n
units
at time (t
+Δt )
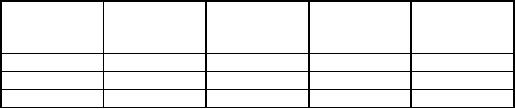
No.
of units
No.
of
No.
of
No.
of units
Case
at
time t
arrivals
services
at
time (t
+
t)
1
0
0
n
n
2
n+1
0
1
n
3
n-1
1
0
n
The
probability of a service rate is μΔt and
that of an arrival rate is λΔt and
(
Δt
) → 0
2
Since
the probabilities are independent we
use the multiplication
theorem in probability
⎛
Probability
⎞
⎛
Probability
⎞ ⎛
Probability
⎞
⎟ � ⎜
⎟�⎜
Probability
of case 1 = ⎜
⎟
⎝
of
n
at
time t
⎠
⎝
of no
arrivals ⎠
⎝ of
no service ⎠
=
⎡Pn (t )⎤ (1-λΔt
) (1-μΔt
)
⎣
⎦
=
Pn (t )
⎡1-λΔt
-μΔt
+λμ (Δt )2 ⎤
⎢
⎥
⎣
⎦
(t )(μΔt
)
=P
n+1
⎛
Probability
⎞
⎛
Probability
⎞ ⎛
Probability
⎞
� ⎜
⎟�⎜
Probability
of case 2 = ⎜
⎟
⎟
⎝
of
n+1 at time
t
⎠
⎝
of no
arrivals ⎠
⎝ of
one service⎠
=
⎡ Pn+1(t
)⎤ [1-λΔt
] ⎡μΔt
⎤
⎣
⎦
⎣
⎦
228
Operations
Research (MTH601)
229
=
Pn+1
(t
)
⎡μΔt
-μλ (Δt )2 ⎤
⎢
⎥
⎣
⎦
=
Pn+1
(t
)
(
μΔt
)
Probability
Probability
Probability
�
�
Probability
of case 3 =
of
no service
of
(n
-
1) at
time t
of
one arrivals
(1-μΔt
)
(λΔt
)
=
Pn-1
(t )
(λΔt
)
=
Pn-1
(t )
2
All
other possibilities or combinations
except the above three
cases will be involving the
term (Δt )
which
tends to zero. As an example, let us
take a combination to have n
units on hand at time
t
then
have one
arrival
and one service being
completed during Δt .
Then
=
Pn (t +
Δt
)
=
Pn (t )(μΔt
)
(λΔt
)
Probability
of this case
2
μλ
=
P
(t )
(Δt )
=
0
n
Now
adding all three cases we
find Pn (t +
Δt
)
given
by
=
P
(t +
Δt
)
=
P
(t
+Δt ) = P
(t )(1
-
λΔt
-
μΔt
)
n
n
n
(t )(μΔt
)
+
P
(t )(λΔt
)
+P
n+1
n-1
This
will lead to the result what
we wanted in Step 1 i.e. to
find Pn(t)
in terms of λ
and
μ
.
Recall the
assumption
that the mean arrival rate
and service rate are
independent of time. This implies that
the probability
of
n
units
in the system at time
t
is
the same as at time (t
+
Δt
)
. Thus Pn (t )
=
Pn (t +
Δt
)
. Use
this in the above
equation,
P
(t )
=
P
(t )(1
-
λΔt
-
μΔt
)
+
P
(t )(μΔt
)
+
P
(t )(λΔt
)
n+1
n-1
n
n
Solving
for Pn+1
(t )
, we
get
(t )μΔt
=
P
(t )Δt (λ +μ
) - P
(t )λΔt
P
n+1
n-1
n
λ+μ
λ
=
P
(t )
-
P
(t )
Pn+1(t)
μ
μ
n-1
n
The
expression gives the probability of
(n+1)
units as a function of the last
two stages n
and
n
-
1. Still
we
need to find a general
expression for Pn(t)
which can be determined in
the following manner.
First
find P1(t)
in terms of P0(t)
and λ
,
μ
.
229

Operations
Research (MTH601)
230
Consider
the two possible cases
for nobody in the system at
time (t
+Δt ) i.e.
P0 (t
+
Δt
)
. They
are;
Case
(1) none at time t, no
arrivals, no service.
Case
(2) one at time t, no
arrivals, one
service.
For
the above two cases we
have the
probabilities.
Case
(1): P0(t)
(1-λΔt
) (1)
Note
that if no units were in the
system, the probability of no service
would be 1,
Case
2: P
(t )
(1-λΔt
) ( μΔt
)
1
P
(t +
t
)
=
case
1 and case 2
0
=
P
(t )
(1-λΔt
) (1)
+
P
(t -
λΔt
)μΔt
0
1
=
P
(t )
-
P
(t )λΔt
+
P
(t )μΔt
+
P
(t )λμ
( Δt
)
2
0
0
1
1
2
=
P
(t )
-
P
(t )λΔt
+
P
(t )μΔt
as (Δt )
→
0
0
0
1
We
know that
P
(t +
Δt
)
=
P
(t )
0
0
P
(t )
-
P
(t )λΔt
+
P
(t )μΔt
=
P
(t )
0
0
1
0
Solving
for P1(t),
we get
P
(t )μΔt
=
P
(t )
+
P
(t )λΔt
1
0
0
λ
P
(t )
=
P
(t )
μ
1
0
From
the above step, we can
develop an expression for
Pn(t)
in terms of P0, λ
and
μ
.
Omitting the
time
notation due to the
independence assumption
P
(t
) = P
(any
time t)
0
0
We
write P0 (t) =
P0
λ
P
=P
μ
1
0
λ
+μ
λ
P
=P
-P
μ
0μ
2
1
λ
+μ
λ
=P
-P
μ
n-1
μ
n
from
Pn+1
230
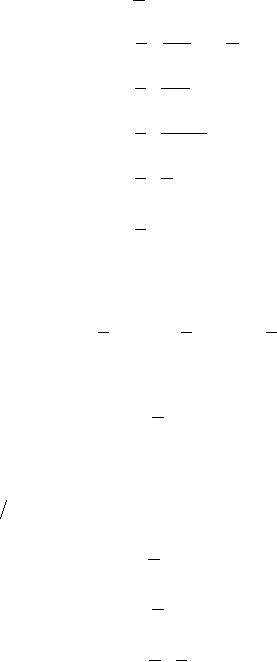
Operations
Research (MTH601)
231
λ
But
P1 = P0
μ
⎛
λ ⎞ ⎛
λ +μ
⎞
λ
P
=
P
⎜
⎟⎜
⎟
- P0
μ
0 μ
⎝
⎠⎝ μ ⎠
2
⎛
λ ⎞ ⎛
λ +μ
⎞
=
P
⎜
⎟⎜
-1⎟
0 μ
⎝
⎠⎝ μ
⎠
⎛
λ ⎞ ⎛
λ +μ
-μ ⎞
=
P
⎜
⎟⎜
⎟
0 μ
⎝
⎠⎝ μ
⎠
⎛
λ ⎞⎛
λ ⎞
=
P
⎜
⎟⎜ ⎟
0 μ
⎝
⎠⎝ μ ⎠
2
⎛λ⎞
=P ⎜
⎟
0 μ
⎝⎠
Similarly
we have
3
4
5
⎛λ⎞
⎛λ⎞
⎛λ⎞
P
=P ⎜
⎟
P
⎜
⎟ ,P =
P
⎜
⎟
,P
=
0 μ
0 μ
0 μ
3
4
5
⎝⎠
⎝⎠
⎝⎠
In
general we have
n
⎛λ⎞
P
=P ⎜
⎟
0 μ
n
⎝⎠
The
above equation gives
Pn in terms of P0, λ
and
μ
.
Finally we have to find an
expression for P0 in
terms
of λ
and
μ
.
We know that the probability of a
busy system is the ratio of
the arrival rate and service
rate,
λ
μ .
Thus the probability of an empty or
idle system is P0.
λ
P
=
1-
μ
0
n
⎛λ⎞
P
=P ⎜
⎟
Since
0 μ
n
⎝⎠
n
⎛
λ ⎞⎛
λ ⎞
P
=
⎜1- ⎟ ⎜
⎟
With
this we complete the step
1.
We
write
⎝
μ ⎠⎝
μ ⎠
n
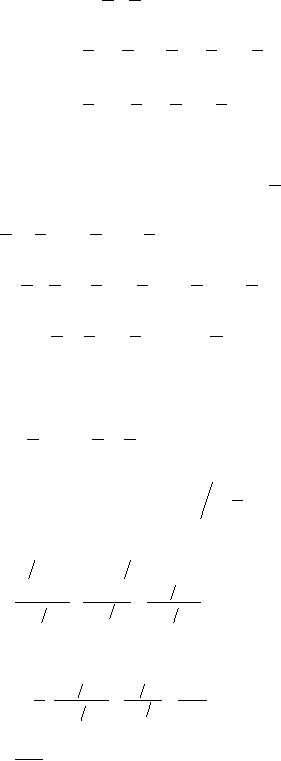
Now
we proceed to step 2. The
expected number of units in
the system is found using
the concept of
expected
value,
∞
E
(
x)
= ∑
xi
Pi
i=0
∞
L=
∑ n
P
n
n=0
231
Operations
Research (MTH601)
232
n
⎛
λ ⎞⎛
λ ⎞
L
=
∑ n⎜1- ⎟ ⎜
⎟
⎝
μ ⎠⎝
μ ⎠
⎛
λ ⎞ ⎡ ⎛
λ ⎞0
⎛
λ ⎞ ⎛ λ
⎞2
⎛
λ ⎞3
⎤
=
⎜1- ⎟ ⎢0⎜ ⎟
+1⎜
⎟+2⎜ ⎟
+3⎜ ⎟
+
⎥
⎝
μ⎠⎢
⎝μ⎠ ⎝μ⎠
⎝μ⎠
⎝μ⎠
⎥
⎣
⎦
⎛
λ ⎞ ⎡
⎛ λ ⎞ ⎛ λ ⎞2
⎛
λ ⎞3
⎤
=
⎜1- ⎟ ⎢0+⎜
⎟+2⎜ ⎟
+3⎜ ⎟
+
⎥
⎝
μ⎠⎢
⎝μ⎠ ⎝μ⎠
⎝μ⎠
⎥
⎣
⎦
Let
the expression in the
parenthesis be = x.
The expression in x,
being a geometric series,
can be
λ
evaluated
in the following way.
Multiply both sides
by
.
Then we have
μ
2
3
4
λ
⎛λ⎞
⎛λ⎞
⎛λ⎞
x
=
⎜ ⎟ + 2⎜ ⎟ +
3⎜ ⎟
+
μ
⎝μ⎠
⎝μ⎠
⎝μ⎠
2
2
2
3
⎛λ⎞
⎛λ⎞
⎛λ⎞
⎛λ⎞
λλ
x
-
x
=
+ 2⎜ ⎟ - ⎜
⎟ + 3⎜ ⎟ -
2⎜ ⎟
+
μμ
⎝μ⎠
⎝μ⎠
⎝μ⎠
⎝μ⎠
2
3
λ
⎛λ⎞
⎛λ⎞
λ
<
1
or λ
< μ ,
=
+⎜ ⎟ +⎜ ⎟ +
As
μ
μ
⎝μ⎠
⎝μ⎠
We
have an infinite geometric
series, with common ratio
less than 1. Adding 1 to
each side, we have
2
λ
⎛λ⎞
λ
x-x
+1 = 1+ + ⎜
⎟
μ
μ
⎝μ⎠
λ⎞
⎛
The
summation of the right side is
1 ⎜1- ⎟
μ
⎝
⎠
Solving
for x
we
get
x(1
-
λ μ )
+
1
=
1
/(1 -
λ μ )
λμ
1
1
x=
-
=
1-(λ
μ )
(1-λ μ )2
(1-λ μ )2
Substitute
the value of x
in
the expression for L.
Then we get
⎛
λ⎞
λ
μ
λμ
λ
L
=
⎜1-
⎟
=
=
⎝
μ ⎠
1-(λ
μ )2 1-λ μ
μ
-λ
λ
L=
μ
-λ
Step
3
We
have to derive the other
expression of Lq, W,
Wq, Ln
and
Wn in
terms of λ
and
μ
.
The derivations
will
be as follows:
232

Operations
Research (MTH601)
233
The
expected system time
W
is
expected
number in system
=
arrival
rate
L
λ = λ λ
(μ
-λ )
=
1
(μ
-λ )
The
expected time in queue
Wq is
Wq =
expected time - time in
serve
1
1
1
W-
=
-
μ
μ
-λ
μ
λ
=
μ
(μ
-λ )
The
expected number in queue
Lq is
Lq =
expected number in system -
expected number in service
λ
λ
μλ -λ (μ
-λ )
=
-=
μ
-λ
μ
μ
(μ
-λ )
μλ
-λμ
+λ 2
λ2
=
=
μ
(μ
-λ )
μ
(μ
-λ )
In
the above expression, the
expected number in service is 1
time the probability that
the service unit is
busy
or 1
The
expected number in a non-empty
queue Ln
Expected
number in queue
L =
Probability
that the queue is not
empty
n
But
the probability of non-empty
queue
=
1-
P
0
=
1
-
1(1
-
λ μ )
=λ μ
λ
λ2
λμ
L =
=
μ
-λ
μ
(μ
-λ )
n
The
expected waiting time for a
non-empty queue Wn is
expected
time in queue
W =
probability
of waiting
n
233
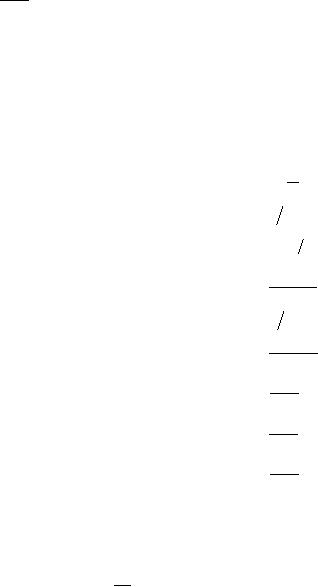
Operations
Research (MTH601)
234
1
=
μ
-λ
In
a single server queueing
model, with assumptions of
Poisson arrival and Poisson
service rate,
infinite
queueing type of problem and
(λ
/
μ
)
<
1
the
following is the summary of formula
used for analysis.
The
assumption
of Poisson arrival and the
service rate are also
equivalent to the exponential
inter-arrival time and
exponential
service time.
RESULTS
FOR POISSON ARRIVAL AND
EXPONENTIAL SERVICE
TIME
λ
P0 =
1
-
1.
The
probability of an empty system
μ
ρ
=λ μ
2.
The
traffic intensity or system
utilization,
Pn =
P0 (λ μ )
n
The
probability on n customers in the
system
3.
λ2
=
The
expected number in the
queue
4.
Lq
μ
(μ
-λ )
=
λ μ -λ
5.
The
expected number in the
system,
L
λ
=
6.
The
expected time in the
queue
Wq
μ
(μ
-λ )
1
=
The
expected waiting time in the
system
7.
W
μ
-λ
λ
=
The
expected number in the
nonempty queue,
8.
Ln
μ
-λ
1
=
The
expected time in the queue
for nonempty queue,
Wn
9.
μ
-λ
The
probability of waiting time more
than or equal to t.
10.
∞
⎛ λ ⎞ (
λ - μ
)w
=
∫ ⎜1-
⎟λ e
dw
t
⎝
μ⎠
P
(waiting
time ≥
t )
The
probability of waiting time in the
system
11.
(
λ -
μ )v
∞
∫
( μ
-λ )
e
dv
P
(waiting
time ≥
t )
=
t
Example
(a)
A repairman is to be hired to repair
machines which break down at
an average rate of 6 per
hour.
The
breakdowns follow Poisson distribution.
The nonproductive time of a
machine is considered to cost
Rs. 20
per
hour. Two repairman, Mr.
X
and
Mr. Y
have
been interviewed for this purpose.
Mr. X
charges
Rs. 10 per
hour
and he services machines at
the rate of 8 per hour.
Mr. Y
demands
Rs. 14 per hour and he
services at an
average
rate of 12 per hour. Which
repairman should be hired?
(Assume 8 hours shift per
day).
234

Operations
Research (MTH601)
235
Solution:
λ
= 6
per hour
Cost
of idle machine hour = Rs.
20
For
Mr. X:
μ
= 8,
Hourly
charges = Rs. 10
Average
number of units in the
system
λ
6
6
=
=
=
=3
μ
-λ
8-6
2
Machine
hours lost in 8 hour shift = 3 x 8 = 24
machine hours
Total
cost = hiring charges of
repairman + cost of idle
time
=
10 x 8 + 24 x 20 = 80 + 480 = Rs.
560
For
Mr. Y:
μ
= 12,
Hourly
charges = Rs. 14/-
Average
number of units in the
system
λ
6
6
=
=
=1
μ
-λ
12-6
6
Machine
hours lost in 8 hours shift
= 1 x 8 = 8
Total
cost = 14 x 8 + 20 x 8 = 112 + 160 =
Rs. 272
Obviously
Mr. Y should be
hired.
Example
A
fertilizer company distributes its
products by trucks loaded at its
only loading station. Both
company
trucks
and contractor's trucks are
used for this purpose. If
was found that on an average
every 5 minutes one
truck
arrived and the average
loading time was 3 minutes.
40% of the trucks belong to
the contractors.
Making
suitable
assumptions determine.
(1)
The
probability that a truck has to
wait.
(2)
The
waiting time of a truck that
waits.
(3)
The
expected waiting time of
contractor's trucks per
day.
Solution:
Following
assumptions are made for
solving the given queueing
model:
(1)
The
arrival rate is randomly distributed
according to Poisson distribution.
235
Operations
Research (MTH601)
236
The
mean value of the arrival
rate is λ
.
(2)
The
service time distribution is approximated
by an exponential distribution and the
rate of service is
(3)
μ.
(4)
The
rate of service is greater
than the rate of
arrivals.
(5)
The
queue discipline is
first-come-first-served.
(6)
The
place of loading the trucks
is only one i.e., there is
only one service
channel.
(7)
The
number of trucks being
served is infinite.
(1)
It
is given that
60
Average
arrival rate =
λ =
=
12 /
hour
5
60
Average
service rate =
μ =
=
20 /
hour
3
Probability
that a truck has to wait is
given by the probability of a busy
system.
λ
12
ρ=
=
=
0.6
i.e.,
μ
20
The
waiting time of a truck that
waits is given by
(2)
1
1
1
W =
=
=
Hour
= 7.5 minutes
μ
-λ
20-12
8
s
It
is given that 40% of the
total trucks belong to the
contractor. Hence the
expected waiting
(3)
time
of contractor's trucks per
day (assuming 24 hours
shift).
=
(no of trucks per day) x
(contractor's percentage)
x
(Expected waiting time of a
truck).
λ
40
=
12
�
24
�
�
100
μ
(μ
-λ )
12
3
=
288
�
0.4
�
=
288
�
0.4
�
20(20-12)
5�8
=
8.64
hours per day.
Example
In
a Bank, every 15 minutes one
customer arrives for cashing
the cheque. The staff in the
only payment
counter
takes 10 minutes for serving
a customer on an average. State
suitable assumptions and
find.
(1)
The
average queue length.
(2)
Increase
in the arrival rate in order to
justify for second counter
(when the waiting time of
a
customer
is atleast 15 minutes the
management will increase one
more counter).
Solution:
The
assumptions are as in the
previous example.
236

Operations
Research (MTH601)
237
60
Arrival
rate, λ
=
=
4
per
hour
(i)
15
60
Service
rate, μ
=
=
6
per
hour
(ii)
10
As
λ
< μ using
M /
M
/
1 / ∞
queueing
models, the average queue
length is given by
λ2
4�4
16
L=
=
=
=
1.33
units
μ
(μ
-λ )
6(6-4)
6�2
The
average waiting time for
the present system is
(iii)
λ
4
4
1
=
=
=
=
hrs
= 20 mts.
μ
(μ
-λ )
6(6-4) 12
3
Since
the management will increase
one more counter if the
waiting time is atleast 15
minutes. The
second
counter is justified at the existing
arrival rate.
Example
A
duplicating machine maintained for
office use is used and
operated by people in the
office who need
to
make copies, mostly by
secretaries. Since the work
to be copied varies in length
(number of pages of
the
original)
and copies required, the
service rate is randomly distributed,
but it does approximate a
Poisson having
a
mean service rate of 10 jobs
per hour. Generally the
requirements for use are
random over the entire 8
hour
work
day but arrive at a rate of
5 per hour. Several people
have noted that a waiting
line develops
occasionally
and
have questioned the policy
of maintaining only one unit. If the
time of a secretary is valued at
Rs. 3.50 per
hour,
make a analysis to
determine
(a)
equipment
utilization
(b)
the
per cent time that an
arrival has to wait
(c)
the
average system time
(d)
the
average cost due to waiting
and operating the
machine.
Solution:
The
arrival rate λ
is
5 per hour and the
service rate μ is
10 per hour
(a)
The
equipment utilization is
ρ
= 5
10 =
0.50
Thus
the equipment is in use 50
per cent of the time.
(b)
The
per cent time an arrival has
to wait is simply the per
cent time that it is busy =
0.50
(c)
The
average system time
W
1
1
1
1
W=
=
=
=
= 0.20
hours
μ
-λ
10-5
10-5
5
237
Operations
Research (MTH601)
238
The
average arrival will spend
0.20 hour in waiting and
processing the job.
(d)
The
average cost per day =
number of jobs processed per
day
x
average cost period
Average
cost per job
=
Average time per job x
Rs. per hour
=
W (Rs. 3.50/hour) = 0.20
(3.50)
Cost
per day = 8(5) (0.20)
(3.50) = Rs. 28 per
day.
Example
At
a public telephone booth in a
post office arrivals are
considered to be Poisson with an
average inter-
arrival
time of 12 minutes. The
length of a phone call may
be assumed to be distributed exponentially
with an
average
of 4 minutes.
(a)
What
is the probability that a fresh arrival
will not have to wait
for the phone?
(b)
What
is the probability that an arrival will
have to wait more than 10
minutes before the phone is
free?
(c)
What
is the average length of
queues that form time to
time?
Solution:
It
is given
1
λ=
=
0.085
per
min
ute
12
1
μ
= = 0.25
per
min
ute
4
λ
=
4 12
=
1 3
=
0.33
=
ρ
μ
Therefore,
we have
(a)
The
probability that a fresh arrival will
not have to wait
=
1
-
P(w >
0)
=
1
-
ρ
=
1
-
0.33
=
0.67
(b)
The
probability for an arrival to have to
wait for atleast 10 minutes
is given by
238

Operations
Research (MTH601)
239
∞
-(
μ
-λ )t
=
∫ (λ
μ )
(μ
- λ )
e
dt
10
∞
-0.165t
=
∫ (0.33)
(0.25 -
0.085)
e
dt
10
∞
⎡
e-0.165t ⎤
=
0.5445
⎢
⎥
= 0.19
⎢
-0.165
⎥
⎣
⎦10
(c)
The
average length of queues
from time to time is given
by
λ
0.85
=
=
=
0.52
μ
-λ
0.25-0.085
EXERCISES
1.
a)
A management has to decide
which of the two repairmen X
or Y to hire. The frequency of
machine
breakdown
in the plant is known to
follow the Poisson distribution at a
rate of 1 machine per
hour.
Repairmen
X charges Rs. 12 per hour. X
is able to repair machines at a
rate charges Rs. 12 per
hour. X is
able
to repair machines at a rate of
1.8 machines per hour
and Y is able to repair
machines at a rate of
1.2
machines
per hour. Assume there is
infinite number of machines.
What is the decision?
2.
The
belt snapping for conveyors
in an open cast mine occur at
the rate of 2 per shift.
There is only one
hot
plate available for
vulcanizing and it can vulcanize on an
average rate of 5 belts per
shift.
(i)
What
is the probability that one
hot plate is readily
available?
(ii)
What
is the average number in the
system?
(iii)
What
is the total system
time?
3.
A
repair shop attended by a
single mechanic has an
average of four customers an hour
who bring small
appliances
for repair. The mechanic
inspects them for defects
and quite often can
fix them right away
or
otherwise
render a diagnosis. This takes
him six minutes on the
average. Arrivals are
Poisson and service
time
has the exponential
distribution.
(a)
Find
the proportion of time
during which the shop is
empty.
(b)
Find
the probability of finding atleast 1
customer in the shop.
(c)
What
is the average number of
customers in the
system?
(d)
Find
the average time, including
services.
4.
a)
For
each of the following,
select the correct
alternative:
(i)
If on an average 10 customers join a
queue in one hour and
the average service time
per
customer
is 6 minutes, then the
average waiting time of a new arrival in
M/M/1 queue is
one
hour.
(A)
True
(B)
False
(C)
Cannot say
(ii)
In an M/M/1 queue, the
service system is busy 75%
of the time and the
inter-arrival time of
customers
is 4 minutes.
(A)
4.5 minutes (B) 4
minutes (C)3 minutes (D) 2
minutes
239
Operations
Research (MTH601)
240
b)
Problems
arrive at a computing centre in
Poisson fashion with a mean
arrival rate of 25 per
hour.
The average computing job
requires 2 minutes of terminal time.
Calculate the
following:
(i)
Average
number of problems waiting
for the computer.
(ii)
The
per cent of times on arrival
can walk right it without
having to wait.
MULTI
CHANNEL SERVICE INFINITE
QUEUE
If
we have more than one
service counter, each with
mean service rate and
with an arrival rate
both
following
Poisson distribution, we have the
following formulae in solving the
problems. The derivation of
these
formulae
is more complicated than
that for a single server
model
1.
The
probability of an empty or idle
system,
1
P =
⎡n=k -1 ⎛
⎞n ⎤ 1 ⎛ ⎞k
k μ
0
⎢
∑ 1
⎜
λ ⎟ ⎥+ ⎜
λ ⎟
⎢
n=0 n!⎝ μ ⎠ ⎥
k
!⎝ μ ⎠
k
μ -λ
⎣
⎦
The
probability that an arrival has to wait
(the probability that there
are k or more units in the
system) is
2.
k
kμ
1
⎛λ⎞
P =
⎜ ⎟
P
k
!
⎝
μ ⎠
k
μ -λ
0
k
The
expected number in the
system
3.
λμ
(λ μ
)k
P
+λ
L=
μ
0
2
(k -1)!(k
μ -λ
)
The
expected number in the queue
is
4.
λμ
(λ
μ )k
P0
L =
q
(k -1)!(k
μ -λ
)2
The
expected time in the queue
is
5.
μ
(λ
μ )k
P0
W =
q
(k -1)!(k
μ -λ
)2
The
expected time in the system,
is
6.
μ
(λ
μ )k
P0
1
W=
+
μ
(k -1)!(k
μ -λ
)2
n
1
⎛λ⎞
P =
⎜ ⎟
P
,
n
=
0, 1,
2, ..., k
-
1
7.
n!
⎝
μ ⎠
0
n
240
Operations
Research (MTH601)
241
⎛λ⎞
1
P=
⎜
⎟ n
P0 , n
≥
k
⎝μ⎠
k
!k
n-k
Example
An
insurance company has three
claims adjusters in its branch
office. People with claims
against the
company
are found to arrive in a
Poisson fashion, at an average
rate of 20 per 8 hour day.
The amount of time
that
an adjuster with a claimant is found to
have an exponential distribution, with
mean service time 40
minutes
Claimants
are processed in the order
of their appearance.
(a)
How
many hours a week an adjuster
expected to spend with
claimants?
(b)
How
much time, on the average,
does a claimant spend in the
branch office?
Solution:
5
λ=
per
hour
2
a)
3
μ=
services
per hour
for
each adjuster
2
From
formula
1
24
P =
=
0
2
3
⎛
5
⎞
1
⎛
5
⎞
1
⎛
5
⎞
9 2
139
1+⎜ ⎟+ �⎜ ⎟ + �⎜ ⎟
�
⎝
3⎠ 2 ⎝ 3⎠ 6
⎝
3⎠ 4
2
The
expected number of idle
adjusters at any specified
time is 3 when nobody is
present, 2 when one
is
at
the counter and 1 when
two are being serviced
with the probabilities of P0, P1 and P2 respectively.
n
1
⎛λ⎞
P =
⎜ ⎟
P
,
n
=
0, 1,
2, ..., k
-
1
The
formula
n!
⎝
μ ⎠
0
n
1
⎛
5
⎞1
24
40
P =
⎜ ⎟
=
1
⎝
3
⎠
139
139
1
1
⎛
5
⎞2
24
100
P =
⎜⎟
=
2
⎝
3
⎠
139
417
2
Expected
number of idle adjusters
is
24
40
100
4
3P +
2
p
+
1P =
3.
+2
=
1.
=
1398
139
417
3
0
2
1
Then
the probability that at any
time one adjuster will be
idle is (
4
3)
� (1
3)
= 4
9 . Expected
weekly
time
spent by the adjuster is
(5
9)
� 40
=
22.2
hours
per week.
b)
The
average time an arrival spends in
the system = system
time
241
Operations
Research (MTH601)
242
k
⎛λ⎞
μ⎜ ⎟
⎝μ⎠
1
=
P +
(k -1)!(k -λ )2 0 μ
⎡
⎤
3⎛ 5 ⎞3
⎢
⎥
⎢
2⎜ 3 ⎟
⎝
⎠ � 24
+
2
⎥ �
60
=
49
=⎢
min
utes
⎥
2
⎢
2!⎛ 9 - 5 ⎞ 139
3 ⎥
⎢
⎜ 2
2⎟
⎥
⎣ ⎝
⎠
⎦
EXERCISES
1.
An
office has to decide whether
to go in for a larger duplicating machine
in place of two small
machines.
The
jobs arrive at the rate of 5
per hour. The data
about the service rate
and daily rental cost
are given
below.
What
is the decision?
Service
Rate per Hour
Daily
Rental Cost
________________________________________
Small
(present) M/c
7
Rs.
50
Large
M/c
11
Rs.
100
2.
A
certain queueing system has
a poisson input with a mean arrival
rate of two per hour.
The service time
distribution
is exponential with a mean of
0.4 hour. The marginal
cost of providing each server is
Rs. 4
per
hour where it is estimated
that the cost of each
unit being idle is Rs.
100 per hour. Determine
the
number
of servers that should be
assigned to the system to
minimize the expected total
cost per hour.
3.
A
telephone exchange has two
long distance operators. The
telephone company finds that
during the peak
period,
long distance calls arrive in a
poisson fashion at an average
rate of 15 per hour. The
service time
is
exponential with a mean of 5 minute
per call, what is the probability
that a subscriber will have
to wait
for
his long distance call
during peak period? What is
the expected waiting time
including service.
MULTI
CHANNEL QUEUE WITH FINITE
POPULATION:
In
this case it is assumed that
the number of channels k is
more than 1, such that 1<
k
<
M.
The
probability
P0 of an empty system
is
1
P0 =
n=k -1
⎡
n
⎤ n=M
⎡
⎛λ⎞
⎤
n
M!
⎛λ ⎞
M!
⎢
⎥+
∑ ⎢
⎜
⎟ ⎥
∑
⎜⎟
⎢
(
M
-n)!n!⎝
μ ⎠
⎥
n=k ⎢ (
M
-n)!k !k n-k ⎝ μ ⎠
⎥
n=0
⎣
⎦
⎣
⎦
The
probability Pn of n
customers
in the system is
n
⎛λ⎞
M!
Pn =
P0
where
0 ≤
n
≤
k
⎜⎟
(M -n)!n!
⎝
μ ⎠
242
Operations
Research (MTH601)
243
n
⎛λ⎞
M!
Pn =
P0
where
k
≤
n
≤
M
⎜⎟
⎝μ⎠
(M -n)!k !k
n-k
Note
that n
cannot
be greater than M.
The expected number
L
of
customers in the system
is
⎛
n=k -1 ⎞
n=k -1
n=m
L
=
∑ nPn + ∑ (
n-k )
Pn +k ⎜1- ∑
Pn ⎟
⎜
⎟
⎝
n=0
⎠
n=0
n=k
The
expected number of customers
Lq in
the queue is
n=M
Lq = ∑ (
n-k )
Pn
n=k
Example
A
repairman services three
machines. For each machine
the time between service
requirements is 8
hours
following exponential distribution. The
time of repair also has
the same distribution with a
mean of 2
hours.
The downtime for a machine
costs Rs. 100 per
hour.
(a)
the
expected number of machines in
operation
(b)
the
expected cost of downtime
per day.
Solution:
First
find λ
and
μ
a)
1
=8
λ
=
0.125
λ
1
=2
μ
=
0.5
μ
1
=
P0
n=3
⎡
3!
⎛
0.125
⎞n
⎤
∑⎢
⎟ ⎥
⎜
⎢
(3-n)!
⎝
0.5
⎠
⎥
n=0
⎣
⎦
1
=
1+0.75+0.375+0.094
=
1 /
2.22 =
0.45
The
expected number of machines in
system is
μ
M-
(1
-
P
)
λ
0
0.5
=
3-
(1
-
0.45)
0.125
=
3
-
4
�
0.55
=
0.8
243
Operations
Research (MTH601)
244
0.8
machines are not running.
Hence expected number of
machines running is
2.2
b)
The
expected downtime cost per
day (8 hours)
=
8
�
expected
number �
cost
=
8
�
0.8
�
100
=
Rs.
640
Segment
VIII: Replacement Models
Lectures
40- 41
244
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION