 |
Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL |
| << Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM |
| Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL >> |
Operations
Research (MTH601)
226
INTRODUCTION
It is a common
phenomenon in everyday life to
see a large number of
persons waiting in front of a
booking
counter in a railway station or in a
theatre or in a ration shop to
have some service carried
out. This
formation
of queue occurs whenever the
present demand for a service
exceeds the present capacity
to provide
the
necessary government, industry, schools,
hospitals, etc.
A
decision regarding the
amount of capacity to provide
must be made frequently in industry
and other
places.
It is difficult to predict about an
arrival and the type of
service required. If we provide
too much service,
it
would involve unnecessary
excessive costs. On the
otherhand, if we do not provide
enough service
capacity,
this
will result in a long
waiting line, which proves costly. So we
are interested in reaching an
economic balance
between
the cost of service and
the cost associated with
waiting for the service.
Queuing theory or waiting
line
theory
provides vital information required
for such a decision. For
describing a waiting line
situation queuing
theory
provides a number of alternative
mathematical models.
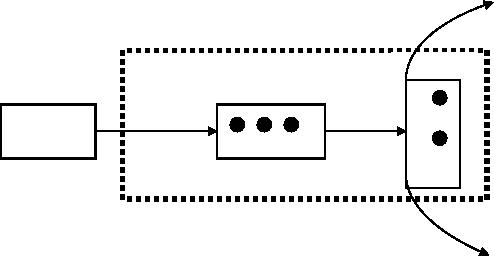
The
basic queuing system
consists of two major components as
shown in figure 1. Customers
arriving
at
a queuing system wait in
queue to get some service,
or if the system is idle or empty,
the arriving customer
may
be serviced immediately. Once
the service is over the
customer leaves the
system.
Served
Units
Service
Queue
Input
Source
Served
Units
The
Basic Queuing
System
DEFINITION
OF TERMS IN QUEUEING
MODEL
Customer:
The
arriving unit that requires
some service to be provided is
called the customer.
The
customer
may represent people,
machines, etc.
Server:
A
server is one who provides
the arriving customer the
necessary service. It may be
persons
in
the counter or machines,
etc.
Waiting
Line or Queue: The
queue represents the number
of customers waiting to be
served.
Normally
the queue does not
include the customer being
served.
Service
Channel: This
refers to the type of
service provided. If we have
one serving unit only,
we
have
a single channel model or
single server model. If
service involves more than
one server, we have a
multi-
channel
server model. We use the
symbol k to denote the number of
service channels.
226
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION