 |
Transportation Problems:REVIEW QUESTIONS |
| << Transportation Problems:DEGENERACY, Destination |
| Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM >> |
Operations
Research (MTH601)
199
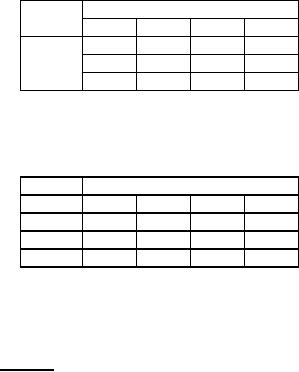
Table
71
Destination
Origin
1
2
3
4
1
-5
-19
2
54
67
3
50
17
(ui +
vj)
for unalloted cells
Table
72
Destination
Origin
1
2
3
4
1
61
67
2
28
14
3
49
54
Cell
evaluation
In
table 72 (matrix of cell
evaluation) there is no negative
entry indicating that the
solution found in
table
66 is optimal.
The
optimum cost = Rs.
6698
REVIEW
QUESTIONS
1.
What
do you understand by degeneracy in a
transportation problem?
2.
What
is degeneracy?
3.
Write
a short note on degeneracy in a
transportation problem.
4.
Explain
how degeneracy in a transportation
problem may be resolved.
5.
How
the problem of degeneracy
arises in a transportation
problem?
6.
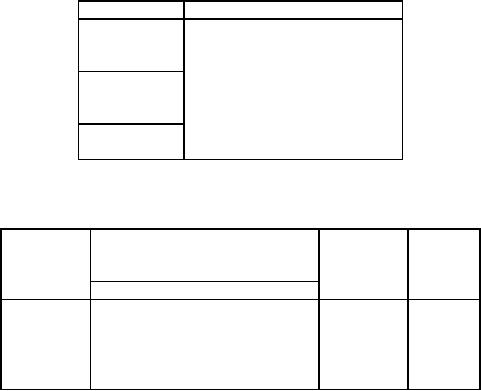
A
company has three plants at
locations A, B and C which
supply to warehouses located at D, E, F,
G
and
H. Monthly plant capacities
are 800, 500 and
900 units respectively.
Monthly warehouse
requirements
are 400, 400, 500,
400 and 800 units
respectively. Unit transportation
costs (in Rupees)
are
given below.
To
D
E
F
G
H
A
5
8
6
6
3
B
4
7
7
6
5
C
8
4
6
6
4
Determine
an optimum distribution for the
company in order to minimize
the total transportation
cost.
199
Operations
Research (MTH601)
200
7.
A
company has four manufacturing
plants and five warehouses.
Each plant manufactures the
same
product,
which is sold at different prices at
each warehouse area. The
cost of manufacturing and
cost of
raw
materials are different in each
plant due to various
factors. The capacities of
the plants are
also
different.
These data are given in
the following table:
Item/Plants
1
2
3
4
Manufacturing
Cost
(Rs.) per
12
10
8
7
unit
Raw
material
Cost
(Rs.) per
8
7
7
5
unit
Capacity
per
unit
time
100
200
120
80
The
company has five warehouses.
The sale prices,
transportation costs and
demands are
given
in the following
table:
Transportation
Cost (Rs.)
Sale
Price
Warehouse
per
unit
(Rs.)
Per
Demand
Plants
Unit
1
2
3
4
80
30
A
4
7
4
3
120
32
B
8
9
7
8
150
28
C
2
7
6
10
70
34
D
10
7
5
8
90
30
E
2
5
8
9
(i)
Formulate this into a transportation
problem to maximize
profit.
(ii)
Find the solution using VAM
method.
(iii)
Test for optimality and find
the optimal solution.
200
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION