 |
Linear Programming:Tie for the Leaving Basic Variable (Degeneracy) |
| << Linear Programming:VARIANTS OF THE SIMPLEX METHOD |
| Linear Programming:Multiple or Alternative optimal Solutions >> |
Operations
Research (MTH601)
143
The
sign or direction of inequality can
easily be reversed when both
sides are multiplied by
-1.
Therefore,
if the constraint has inequality of
the type ( > ), the same
can be converted into the
desired inequality of
the
type ( < ) by multiplying both
sides by -1. To illustrate consider
the inequality 2x
+
5y
>
18. This is equivalent to
-2x -
5y
<
-18. But this may lead to
negative value in the right
side, which makes the
solution infeasible, and we
may
have
to adopt big M
technique
or two-phase technique to find a
feasible optimal solution.
Tie
for the Leaving Basic
Variable (Degeneracy).
The
question may arise as to
which of the basic variable
to be selected to leave the
basis when many
basic
variables
reach zero (as indicated by
equal values in the ratio
column) as the entering basic
variable is being
changed.
Thus there is a tie between or
among the leaving basic
variables. Of course the tie
can be broken
arbitrarily.
This leads, in the next iteration,
the basic
variables
to take value zero, in which
case the solution is
said
to
degenerate.
There is no assurance that
the value of the objective
function will improve (Since the new
solutions
may
remain degenerate).
Consider
the following
example:
Example
Maximize
Z
=
2x
+
5y
Subject
to
x
<
40
y
<
30
x
+ y <
30
x,
y >
0
Introducing
slack variables, the problem
is expressed in the standard
form.
Z
-
2x
5y
=0
(1)
+
S1
=
40
(2)
x
+
S2
=
30
(3)
y
+
S3
=
30
(4)
x+y
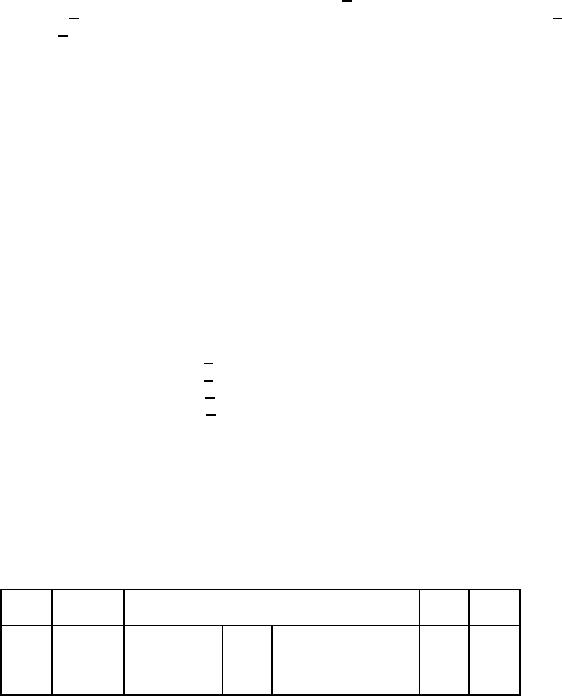
Starting
table
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
-2
-5
0
0
0
0
1
0
1
0
1
0
0
40
∞
S1
2
0
0
1
0
1
0
30
30
S2
3
0
1
1
0
0
1
30
30
S3
There
is a tie between S2 and S3 as to which to be selected as to
which to be selected as leaving
the basis.
Select
arbitrarily S3 as the leaving basic
variable.
First
Iteration: S3 leaves the basis
and y
enters.
143
Operations
Research (MTH601)
144
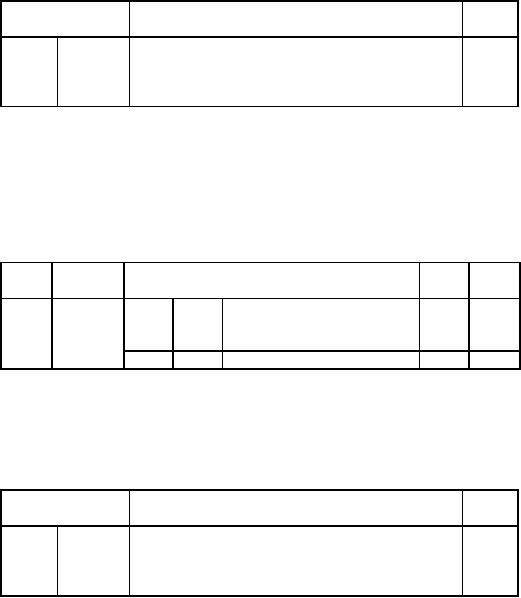
RHS
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
3
0
0
0
5
150
1
0
1
0
1
0
0
40
S1
2
0
-1
0
0
1
-1
0
S2
3
0
1
1
0
0
1
30
y
The
optimal solution is Z*
= 150, S1 = 40, S2 = 0, y
=
30
Note:
One
of the basic variables
S2 in the final table of
the simplex method has a
value equal to zero leading
to a
degenerate
solution.
If
we had taken S2 as the leaving basic
variable then the first
iteration would be as
follows:
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
-2
0
0
5
0
150
1
0
1
0
1
0
0
40
40
S1
2
0
0
1
0
1
0
30
∞
y
3
0
1
0
0
-1
1
0
0
S3
Proceeding
to the second iteration from
this stage, second iteration
will be as follows.
Second
Iteration:
RHS
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
0
0
0
3
2
150
1
0
0
0
1
1
-1
40
S1
2
0
0
1
0
1
0
30
y
3
0
1
0
0
-1
1
0
x
The
final solution is Z*
=
150, S1 = 40, y
=
30, x
=
0.
The
above table (final step)
indicates that the basic
variable x
is
equal
to
0. This implies that if we
have
to
decide the maximum profit
with production of the two
products, even without
producing one product we
still get
the
maximum profit. This is a degenerate
optimal solution.
Note
that the value of the
variables in the first and
second iterations is the
same. At both iterations one
of
the
basic variables is zero. If
there is an indication of degeneracy in
the first iteration itself,
why don't we stop at
the
iteration
when a degenerate solution appears?
But we are not sure
that this will coincide with
the optimal. The
optimal
solution may not be
degenerate.
144
Operations
Research (MTH601)
145
(Temporary
Degenerate Solution)
Example
Minimize
Z
=
2x
+
y
Subject
to
4x +
3y
<
12
4x +
y
<
8
4x -
y
<
8
x,
y
>
0
Solution:
Introducing
slack variables, we
get
Z
-
2x
-
y
=
0
4x +
3y
+
S1 = 12
4x +
y
+
S2 = 8
4x -
y
+
S3 = 8
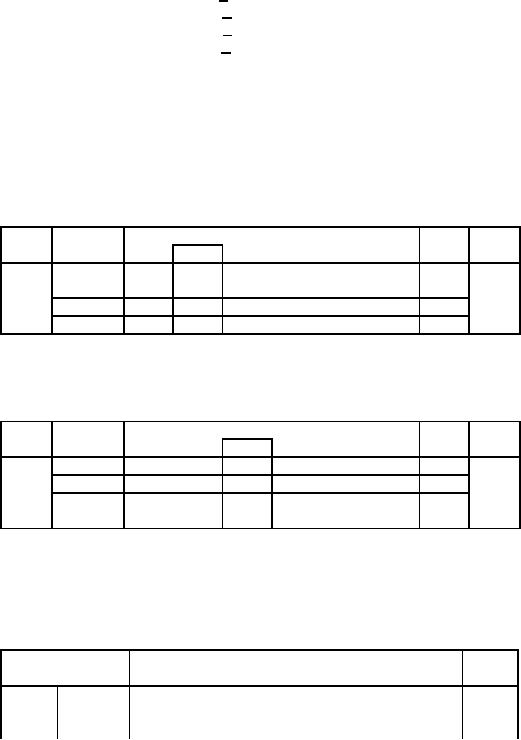
Starting
table:
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
-2
-1
0
0
0
0
1
0
4
3
1
0
0
12
3
S1
2
0
4
1
0
1
0
8
2
S2
3
0
4
-1
0
0
1
8
2
S3
First
Iteration: x enters
the basis and S2 leaves
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
0
-1/2
0
1/2
0
4
1
0
0
2
1
-1
0
4
2
S1
2
0
1
1/4
0
1/4
0
2
8
x
3
0
0
-2
0
-1
1
0
-
S3
Note:
S3
cannot leave the basis
according to the feasibility
condition.
Second
Iteration: y enters
and S1 leaves the
basis.
RHS
Eqn.
Basic
Coefficient
of
No.
Variable
S2
S3
Z
x
y
S1
0
-
1
0
0
1/4
1/4
0
5
1
0
0
1
1/2
-1/2
0
2
y
2
0
1
0
-1/8
-3/8
0
3/2
x
145

Operations
Research (MTH601)
146
3
0
0
0
1
-2
1
4
S3
The
optimal solution is Z
=
5, x
=
3/2, y
=
2, S3 = 4, S1 = S2 = 0.
Note
that the solution in the
first iteration is degenerate
while the solution in the
second and final
iteration
is
non-degenerate. Hence the
problem is temporarily degenerate.
Sometimes
it is possible that the
simplex iterations will
enter a loop which will
repeat the same sequence
of
iterations
without ever reaching an
optimal solution. This
peculiar problem is known as
"cycling" or "circling" in
linear
programming. But the
occurrence of such type of
problem is very rare in practice.
However, there are
procedures
developed to overcome such
situations. Since it is rare
the discussion is
skipped.
Unbounded
solution
In
some of the linear
programming problems the solution
space becomes unbounded so
that the value of
the
objective
function also can be increased
indefinitely without a limit.
But it is wrong to conclude
that just because the
solution
space is unbounded the solution
also is unbounded. The solution
space may be unbounded but
the solution
may
be finite.
The
following two problems illustrate
these aspects.
(unbounded
solution space and unbounded
optimal solution)
Example
Maximize
Z
=
3x
+
2y
Subject
to
x
- y <
15
2x -
y
<
40
x,
y >
0
Solution:
Convert
the given problem into
standard form by including
slack variables. Thus we
have
Z
-
3x
-
2y
=
0
(0)
x
-
y
+
S1 = 15
(1)
2x -
y
+
S2 = 40
(2)
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
Z
x
y
S1
0
-
1
-3
-2
0
0
0
1
0
1
-1
1
0
15
15
S1
2
0
2
-1
0
1
40
220
S2
First
Iteration: x enters
and S1 leaves basis.
Eqn.
Basic
Coefficient
of
RHS
Ratio
146
Operations
Research (MTH601)
147
No.
Variable
Z
x
y
S1
S2
0
-
1
0
-5
3
0
45
1
0
1
-1
1
0
15
-15
x
2
0
0
1
-2
1
10
10
S2
Second
Iteration: y enters
and S2 leaves the
basis.
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
Z
x
y
S1
0
-
1
0
0
-7
5
95
1
0
1
0
-1
1
25
-25
x
2
0
0
1
-2
1
10
-5
y
Now
we have a peculiar situation at
the end of second iteration
in which the objective function
row
indicates
or suggests that S1 is the
entering variable and there
is scope for further
maximizing the value of
objective
function
Z. But we are not in a position to
select the leaving basic
variable, as both the ratios
are negative which
cannot
be taken as feasibility conditions.
Thus we conclude that
without removing either x or y from
the basis we
cannot
further improve the value of
the objective function Z, inspite of
the scope for maximization
as indicated by a
negative
coefficient in the objective row.
Therefore we detect an unbounded solution
to a linear programming
problem
from the simplex table
that if at any iteration,
any of the candidates for
the entering variable have
all
negative
or zero coefficients in the
constraints.
Example
(Unbounded
solution space but bounded
optimal solution)
Maximize
Z
=
3x
- y
Subject
to
x
- y <
10
<
20
x
x,
y >
0
Solution:
Introducing
slack variables and
expressing the problem in
the standard form we
have
Z
-
3x
+
y
=
0
(0)
x
-
y
+
S1 = 10
(1)
x
+
S2 = 20
(2)
Starting
table
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
Variable
S2
Z
x
y
S1
0
-
1
-3
1
0
0
0
1
0
1
-1
1
0
10
10
S1
147
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION