 |
Linear Programming:The Two Phase Method, First Iteration |
| << Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE |
| Linear Programming:VARIANTS OF THE SIMPLEX METHOD >> |
Operations
Research (MTH601)
136
Z*
= 185/11
x1 = 40/11
x2 = 25/11
The
Two Phase Method
A
difficulty is being encountered in
the use of M
technique
in that there is a possible
computational error
that
could result from giving a
very large value of
M.
By this the objective coefficients of
the variables x
and
y
are
now
too small compared with
the large numbers created by
the multiples of M.
The solution may become
insensitive
to
the relative value of the
original coefficients of the decision
variables x
and
y
due
to the round off error
which is
inherent
in any digital computer. The
result could be that both
may have equal coefficients in
the objective function.
To
overcome this difficulty another
method namely two phase
method is presented below.
This method involves
two
phase
which are:
Phase
1:Replace
the original objective problem by
the sum of the artificial
variables to formulate a new
problem.
Then
this new objective function is then
minimized
subject
to the constraints of the
original problem. If the
problem
has
a feasible solution, the minimum
value of the objective function
will be zero which shows
that all the
artificial
variables
are zero. Then proceed to
phase II. Otherwise, if the
minimum value is greater
than zero, we conclude
that
the
problem has no
feasible solution.
Phase
II:
Use
the optimum basic solution of
phase I as a starting solution for
the original problem. Now
the
original
objective function has to be expressed in
terms of the non-basic
variables only. This can be
achieved by
adding
suitable multiples of the
constraint equations involving
artificial variables.
Example
Consider
the problem
Maximize
Z
=
2x
+
5y
Subject
to
x
<
40
y
<
30
x
+ y >
60
x,
y >
0
Solution:
We
try to solve this problem by
the two-phase method.
Introduce
slack variables S1 and S2 for the first
two constraints respectively.
Subtract a slack variable
S3 and
add
an artificial variable A
for
the third constraint so that
the third constraint is changed
into x
+ y -
S3 + A
=
60. In
this
problem we have the new
objective function expressed as
minimization of the sum of
artificial variables. We
have
only one artificial
variable.
Phase
I
Minimize
(0)
Z=A
Subject
to
x
+ S1 = 40
(1)
y
+
S2 = 30
(2)
136
Operations
Research (MTH601)
137
x
+ y - S3 + A
=
60
(3)
Note
that the objective function is always of
the minimization irrespective of
whether the original
problem
is
maximization or minimization of the
objective function.
We
prepare the initial table as
follows:
137
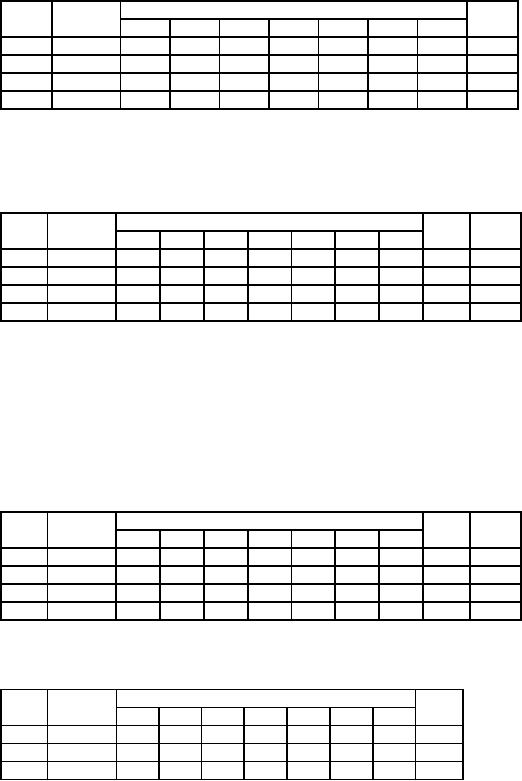
Operations
Research (MTH601)
138
RHS
Eqn.
Basic
Coefficient
of
No.
variable
S2
S3
A
Z
x
y
S1
0
-
1
0
0
0
0
0
-1
0
1
0
1
0
1
0
0
0
40
S1
2
0
0
1
0
1
0
0
30
S2
3
0
1
1
0
0
-1
1
60
A
In
the above table the
objective function has the coefficient of
the basic variable A.
To eliminate the same,
we
multiply the equation 3
involving the basic variable
A
by
1 and add to objective row.
Hence the revised table
his
shown
below.
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
variable
S2
S3
A
Z
x
y
S1
0
-
1
1
1
0
0
-1
0
60
1
0
1
0
1
0
0
0
40
40
S1
2
0
0
1
0
1
0
0
30
∞
S2
3
0
1
1
0
0
-1
1
60
60
A
Solution:
Z
=
60, S1 = 40, S2 = 30, A
=
60, x
= y =
S3 = 0
First
Iteration:
x
or
y
can
enter the basis as they
have the same positive
coefficients. Choose any
one, say x,
and hence S1
leaves
the basis.
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
variable
S2
S3
A
Z
x
y
S1
0
-
1
0
1
-1
0
-1
0
20
1
0
1
0
1
0
0
0
40
∞
x
2
0
0
1
0
1
0
0
30
30
S2
3
0
1
1
-1
0
-1
1
20
20
A
Second
Iteration:
y
enters
and A
leaves
the basis.
RHS
Eqn.
Basic
Coefficient
of
No.
variable
S2
S3
A
Z
x
y
S1
0
-
1
0
0
0
0
0
-1
0
1
0
1
0
1
0
0
0
40
x
2
0
0
0
1
1
1
-1
10
S2
138

Operations
Research (MTH601)
139
3
0
1
1
-1
0
-1
1
20
y
From
the above table we see
that the objective function
Z
=
0 and A
has
left the basis. Hence
A
becomes
a
non-basic
variable. This is the indication that
the problem has a feasible
solution and we can proceed to
phase II,
which
is explained below.
In
the phase II, a table is
prepared with the objective
function and the set of
constraints tabulated
Phase
II:
in
the final table of Phase I
omitting the column of the
artificial variable, as it is
non-basic.
In
preparing the table the
objective function has to be expressed in
terms of the non-basic
variables only. In
other
words,
the coefficients of the basic
variables must be
zero.
Eqn.
Basic
Coefficient
of
RHS
No.
variable
S2
S3
Z
x
y
S1
0
-
1
-2
-5
0
0
0
0
1
0
1
0
1
0
0
40
x
2
0
0
0
1
1
1
10
S2
3
0
0
1
-1
0
-1
20
y
In
the above table, x and
y
are
basic variables and their
coefficients are -2 and -5 respectively.
Hence the
objective
function must be rearranged to make
the coefficients of x
and
y
as
0. This is obtained by multiplying
the
equation
(1) by 2 and the equation
(3) by 5 and adding this to
the objective row. We have
the following starting
table
with
the revised objective
function.
RHS
Ratio
Eqn.
Basic
Coefficient
of
No.
variable
S2
S3
Z
x
y
S1
0
-
1
0
0
-3
0
-5
180
1
0
1
0
1
0
0
40
∞
x
2
0
0
0
1
1
1
10
10
S2
3
0
1
1
-1
0
-1
20
-20
y
The
original problem is one of
maximization and hence in
the first iteration
S3 enters and
S2 leaves the
basis.
First
Iteration:
RHS
Eqn.
Basic
Coefficient
of
No.
variable
S2
S3
Z
x
y
S1
0
-
1
0
0
2
5
0
230*
1
0
1
0
1
0
0
40
x
2
0
0
0
1
1
1
10
S3
3
0
0
1
0
1
0
30
y
We
get the optimum value of
Z
in
the above table as no
negative coefficient is present in the
objective
function
row.
139
Operations
Research (MTH601)
140
Solution:
Z
=
230, x
=
40, y
=
30, S3 = 10, S1 = S2 = 0.
REVIEW
QUESTIONS
1.
An
animal feed manufacturer has to
produce 200 kg of a feed
mixture consisting of
two
ingredients
x1 and x2. x1 costs Rs. 6 per kg
and x2 costs Rs. 16 per kg
Not more than 80 kg of
x1 can be used
and
atleast 60 kg of x2 must be used. Using
simplex method, find how
much of each ingredient
should be
used
in the mix if the company
wants to minimize cost. Also
determine the cost of the
optimum mix.
2.
A
marketing manager wishes to
allocate his annual
advertising budget of Rs.
20000. in two media
vehicles
A
and
B,
The unit of a message in
media A
is
Rs. 1000 and that of
B
is
Rs. 1500. Media A
is
a
monthly
magazine and not more
than one insertion is
desired in one issue. At
least 5 messages
should
appear
in media B.
The expected effective audience
for unit messages in the
media A
is
40000 and for
media
B
is
55000.
(i)
Develop a mathematical
model.
(ii)
Solve it for maximizing the
total effective audience.
3.
A
pension fund manager is
considering investing in two
shares A
and
B.
It is estimated that,
(i)
Share A
will
earn a divided of 12% per
annum and share B 4%
per annum.
(ii)
Growth in the market value
in one year of share
A
will
be 10 paise per Re. 1
invested and in B
40
paise
per
Re. 1 invested.
He
requires investing minimum total
sum which will give
*
dividend income of at least Rs.
600 per annum
and
*growth
in one year of atleast Rs.
1000 on the initial
investment.
Your
are required to
(i)
State the mathematical formulation of
the problem.
(ii)
Compute the minimum sum to
be invested to meet the
manager's objective by using
simplex method.
4.
A
company possesses two
manufacturing plants each of
which can produce three
products x,
y, z
from
a common raw material. However
the proportions in which the
products are produced are
different in
each
plant and so are the
plant's operating costs per
hour. Data on production per
hour and costs are
given
below
together with current orders
in hand for each
product.
Product
Operating
x
y
z
cost/hr
(Rs.)
Plant
A
2
4
3
9
140
Operations
Research (MTH601)
141
Plant
B
4
3
2
10
Orders
50
24
60
on
hand
You
are required to use the
simplex method to find the
number of production hours
needed to fulfill the
order
on hand at minimum
cost.
5.
Maximize
x0 = 2x1 + x2 + x3
Subject
to
2x1 + 3x2 - x3 < 9
2x2 + x3 > 4
x1 + x3 = 6
x1, x2, x3 > 0
6.
Minimize
Z
=
3x1 + 2.5 x2
Subject
to
2x1 + 4x2 > 40
3x1 + 2x2 > 50
x1 , x2 > 0
7.
The
following table gives the
protein, fats and
carbohydrates available in 50 grams of
food items
F1, F2, F3 and F4.
Food
items
Protein
Fats
(gms)
Carbohydrate
(gms)
(gms)
2.4
0.3
15.8
F1
2.3
9.4
0.9
F2
8.4
2.1
0.0
F3
1.6
3.7
18.0
F4
The
price of 50 grams of each of
the four items is as
follows:
F1
F2
F3
F4
Item
5
12
20
20
Price
in paise
The
hospital has recommended
that it is necessary to consume
atleast 75 grams of protein 90
grams of fat
and
300 grams of
carbohydrate.
Solve
the problem to find the
minimum food bill.
8.
Solve
using the two-phase
technique.
141
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION