 |
Linear Programming:LINEAR PROGRAMMING PROBLEM |
| << Linear Programming:VITAMIN CONTRIBUTION, Decision Variables |
| Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING >> |
Operations
Research (MTH601)
96
L
LINEAR
PROGRAMMING PROBLEM
Let
xi = decision variable for
ith
variable.
ci = profit or cost co-efficient of
ith
variable.
Z
=
function to be maximized or
minimized.
Thus
for n
decision
variables, the objective function is to
maximize or minimize
Z
= c1 x1 +
c2 x2 + ... + cn xn
aij = co-efficient of the jth
constraint and ith
variable
Let
bi = resource limitation for
ith
constraint
Thus
the restrictions may be
expressed in the general
form
a11x1
+ a12x2
+ ... +
a1nxn
< b1
a21x1
+ a22x2
+ ...
+a2nxn
< b2
:
:
:
:
am1x1
+ am2x2
+ ...+
amnxn
< bm
and
xi > 0 for all values of
i
from
1 to n
The
same linear programming
problem can be expressed in a
more condensed form using
summation
notation
or matrix equation.
n
Z
=
∑ ci xi
Maximize
i
=1
n
∑
aij x
j
for
all i
=
1, 2, ..., m
Subject
to
j
=i
and
xj >
0 for
all j
=
1, 2, ..., n
or
Maximize
Z
= CX ,
subject to AX
<
B
where
C
is
a row vector and X and
B
are
column vectors. A is a co-efficient matrix of
the order m
x
n.
96
Operations
Research (MTH601)
97
The
linear programming problem
may have an objective
function to minimize cost
also.
The
inequalities may be "greater
than or equal" instead of "less
than or equal". Further in
some
cases,
the restrictions involve
"equalities".
The
successful application of linear
programming is the ability to
recognize that the problem
can be
formulated
as a linear programming
model.
97
Operations
Research (MTH601)
98
REVIEW
QUESTIONS
1.
What
do you understand by Linear
Programming problem?
2.
Explain
how linear programming can
be applied to management
problems.
3.
Explain
the terms: objective function
and restrictions in relation to
linear programming
problem.
4.
Give
a mathematical format in which a linear
programming problem is
expressed.
5.
Enumerate
the limitations of linear
programming problem.
6.
In
relation to linear programming explain
the implications of the
following assumptions of
the
model.
�
Linearity
for the objective function
and constraints.
�
Continuous
variables.
�
Certainty.
7.
Discuss
in brief linear programming as a
technique for resource
utilization.
8.
A
company makes products
A,
B, C and
D
which
flow through four departments:
Drilling, Milling,
Lathe
and Assembly. The variable
time per unit of different
products are given below in
hours:
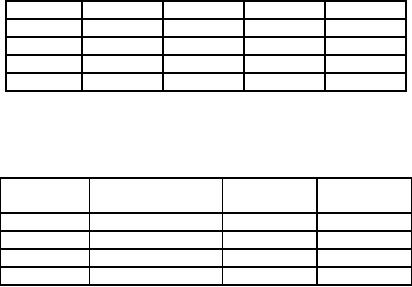
Product
Drilling
Milling
Lathe
Assembly
A
3
0
3
4
B
7
2
4
6
C
4
4
0
5
D
0
6
5
3
The
unit contribution of the four products
and hours of availability in
the four departments
are:
Product
Contribution/Unit
Department
Hours
Rs.
Available
A
9
Drilling
70
B
18
Milling
80
C
14
Lathe
90
D
11
Assembly
100
Formulate
a linear programme for
maximizing the contribution.
9.
A
pension fund manager is
considering investing in two
shares A
and
B.
It is estimated that:
(i)
Share A will earn a dividend of
12% per annum and
share B 4 % per
annum.
98
Operations
Research (MTH601)
99
(ii)
Growth in the market value
in one year of share will be
10 paise per Re. 1 invested
and in B 40
paise
per Re. 1 invested.
He
requires investing the
minimum total sum, which
will give
�
dividend
income of at least Rs. 600
per annum and
�
growth
in one year of atleast Rs.
1000 on the initial
investment.
you
are required to state the
mathematical formulation of the
problem.
10.
A
manufacturer uses three raw
products a,
b, c priced
at 30, 50, 120 rupees
per kg respectively. He
can
make three different products
A,
B and
C,
which can be sold at 90,
100, 120 rupees per
kg
respectively.
The raw products can be
obtained only in limited
quantities, namely 20, 15
and 10 kg
per
day. Given: 2 kg of a plus 1 kg of
b
plus
1 kg of c
will
yield 4 kg of A;
3 kg of a plus 2 kg of b
plus
2kg of c
will
yield 7 kg of B;
2kg of b
plus
1 kg of c
will
yield 3 kg of C.
Make
a production plan, assuming
that the other costs
are not influenced by
the
choice
among the alternatives.
Formulate the model of the
problem.
11.
A
marketing manager wishes to
allocate his annual
advertising budget of Rs.
20,000 in two media
vehicles
A
and
B.
The unit of a message in
media A
is
Rs. 1000 and that of
B
is
Rs. 1500, Media A
is
a monthly magazine and not
more than one insertion is
desired in one issue. At
least 5 messages
should
appear in media B.
The expected effective audience
for unit messages in the
media A
is
40,
000
and media B
is
55, 000.
�
Develop
a mathematical model.
�
Solve
for maximizing the total effective
audience.
12.
A
company produces four products 1 to 4.
Raw material requirements,
storage space needed,
production
rates and profits are given
in the table below. The
total amount of raw
material
available
per day for all four
products is 180 kg, total
space available for storage
is 230 sq. mtr.
and
7 hours/day is used for
production.
1
2
3
4
Raw
materials (Kg/piece)
2
2
1.5
4
Space
(sq. mtr./piece)
2
2.5
2
1.5
Production
rate (pieces/hr)
15
30
10
15
Profit
(Rs./piece)
55
56.6
55
55.5
How
many units of each product
should be produced to maximize total
profit?
13.
A
ship has three cargo
holds, forward, aft and
centre.
The
capacity limits are:
99
Operations
Research (MTH601)
100
Forward
2000
tons
1000
cubic meter
Centre
3000
tons
1350
cubic meter
Aft
1500
tons
300
cubic meter
The
following cargoes are
offered; the ship owners
may accept all or any
part of each
commodity.
100
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION