 |
Operations
Research (MTH601)
80
LINEAR
PROGRAMMING
Linear
programming is a mathematical technique
designed to aid managers in allocating
scarce resources
(such
as labor, capital, or energy) among
competing activities. It reflects, in the
form of a model, the
organization's
attempt
to achieve some objective (frequently,
maximizing profit contribution,
maximizing rate of
return,
minimizing
cots) in view of limited or
constrained resources (available
capital or labor, service levels,
available
machine
time, budgets).
The
linear programming technique
can be said to have a linear
objective function that is to be
optimized
(either
maximized or minimized) subject to
linear equality or inequality constraints
and sign restrictions on
the
variables.
The term linear describes
the proportionate relationship of
two or more variables. Thus,
a given change in
one
variable will always cause a
resulting proportional change in
another variable.
Some
areas in which linear
programming has been applied
will be helpful in setting the climate
for learning
about
this important technique.
(i)
A
company produces agricultural
fertilizers. It is interested in
minimizing costs while
meeting certain
specified
levels of nitrogen, phosphate,
and potash by blending
together a number of raw
materials.
(ii)
An
investor wants to maximize
his or her rate of return by
investing in stocks and
bonds. The investor
can
set
specific conditions that have to be
met including availability of
capital.
(iii)
A
company wants the best
possible advertising exposure
among a number of national
magazines, and radio
and
television commercials within its
available capital
requirements.
(iv)
An
oil refinery blends several
raw gasoline and additives
to meet a car manufacturer's
specifications while
still
maximizing its profits.
(v)
A
city wants to maximize the
daytime use of recreational
properties being proposed
for purchase with a
limited
capital available.
This
technique, called linear
programming (L.P), is solved in a
step-by-step manner called
iterations. Each
step
of the procedure is an attempt to improve
on the solution until the
"best answer" is obtained or
until it is shown
that
no feasible answer
exists.
Formulation
of the Linear Programming
Problem
To
formulate a real-life problem as a linear
program is an art in itself. To
aid you in this task, it is
helpful to
isolate
the essential elements of
the problem as a means of
asking what the clients
wants and what information
can
be
gained from the data
that has been
provided.
The
first step in formulating a problem is to
set forth the objective
called the objective
function.
80
Operations
Research (MTH601)
81
A
second element of a problem is
that there are certain
constraints on the company's
ability to maximize
the
total
contribution. These constraints
are:
(1)
quantity of raw materials
available,
(2)
the level of demand for the
products, and
(3)
the equipment productive
capacity.
A
further element that must be
considered in the problem is
the time period being
used. The duration
may
be
either long term or short
term. Although time is an important
element, it is one that has
flexibility so that the
time
horizon
may be changed as long as the
restrictions are compatible
with the periods under
consideration.
The
last element is that every
product has a likelihood of
being made. These products
are the dependent or
decision
variables. Of course, the
likelihood of a variable's being in
the answer may change
with the price or
contribution
values (usually profit and
the nature of the
restraints. Yet, at this point there is
nothing to indicate
that
differing
chances of occurrence exists
for the possibility of making
each of the products.
The
first stage of solving linear
programming problems is to set forth
the problem in a mathematical
form
by
defining the variables and
the resulting constraints.
Generally, the relationship is
fairly simple using
only
elementary
algebraic notation. The
relationships can be seen by
first identifying the
decision variables. To aid
in
using
algebraic notation, the
decision variables can be
represented by symbols such as X, Y,
Z.
Next,
we must build the objective
function. If the goal is to maximize
profit, we identify our
objective
function
as
Maximize
total profit or Minimize total loss
(cost).
Then
we write problem
constraints.
These
steps are now illustrated by taking
some examples.
Example
1:
Product
Mix
The
Regal China Company produces
two products daily plates
and mugs. The company
has limited
amounts
of two resources used in the
production of these products clay
and labor. Given these limited
resources, the
company
desires to know how many
plates to produce each day,
in order to Maximize profit.
The two products
have
the
following resource requirements
for production and profit
per item produced (i.e.,
the model
parameters).
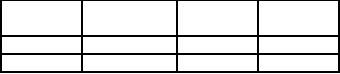
Product
Labor
Clay
Profit
(hours/unit)
(lbs./unit)
(Rs./unit)
Plate
1
4
4
Mug
2
3
5
There
are 40 hours of labour and
120 pounds of clay available
each day for
production.
81
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION