ZeePedia

Inventory Control:Purchasing model with shortages

<< Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
Inventory Control:Manufacturing model with no shortages >>
img
Operations Research (MTH601)
58
= ( Number of orders) × (Cost of one cycle)
= 24(500 × 2) + 100 + (500 / 2 × 0.5 × 0.80)
= Rs. 28800
Model 2 Purchasing model with shortages
In this model, shortages are allowed and consequently a shortage cost is incurred. Let the shortages be
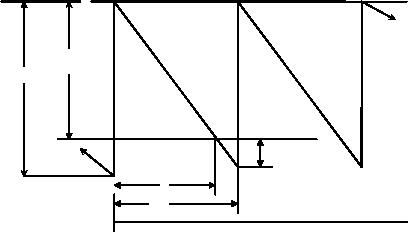
denoted by `S' for every cycle and shortage cost by C4 per item per unit time. This model is illustrated in Fig .3
Im
Q
s
t1
t2
t
T
Fig. 3
Fig. 3 shows that the back ordering is possible (i.e.) once an order is received, any shortages can be made
up as the items are received. Consequently shortage costs are due to being short of stock for a period of time.
The cost per period includes four cost components.
Total cost per period = Item cost + Order cost + Holding cost + Shortage cost
Item cost per period = (item cost) × (number of items/period)
= C1Q
(13)
Order cost per period = C2
Let t1 be the time period during which only the items are held in stock. Let the maximum inventory be denoted by Im
and this is equal to (Q ­ S) or Im = (Q ­ S)
From similar triangle concept, the following equations can be obtained, referring to fig 3
58
img
Operations Research (MTH601)
59
t1 Im = t Q
(16)
Q = t (Q - S ) / Q
t =tI
(17)
or
m
1
t2 S = t Q
t =tS Q
(18)
or
2
Since time of one period t = Q / D
Q-S Q
t =
(19)
QD
1
SQ
t =
(20)
QD
2
Holding cost per period
= Average stock/period × t1 × hotlding cost/unit/unit time
= Im / 2 × t1 × C3
= C3 × (Q-S ) 2 × (Q-S ) Q × Q D
2
C3 (Q - S )
=
(21)
2D
Shortage cost per period
Average shortages/period × t2 × shortage cost
= S 2 × S Q × Q D × C4
= C4 × S  2 2D
(22)
Adding all the four cost components, we get the inventory cost per period.
C3 (Q-S )2  C4S  2
C′ = C1Q + C2 +
+
(23)
2D
2D
Therefore inventory cost per unit of time is obtained by dividing C ′ bye t or Q/D
Therefore,
59
img
Operations Research (MTH601)
60
C1QD  C  2D  C3 (Q-S )2 D  C4S  2 D
C=
+
+
+
2D×Q
Q
Q
2D Q
C2D  C3 (Q-S )2  C4S  2
=C D +
+
+
(24)
Q
2Q
2Q
1
This is an expression involving two variables Q and S. For optimum values of Q* and S*, the function has to be
differentiated partially with respect to Q and S and equated to zero.
∂C
=0
∂Q
C3  C3S  2  C4S  2
-C2D
=
+
-
-
2
Q2
2
2Q2
2Q
S2
C2D  C3
=-
+
-
(C + C )
(25)
Q
2  2Q2    3
4
∂C
=0
∂S
S (C3 +C4 )
C3S  C4S
=-C +
+
= -C +
(26)
Q
Q
Q
3
3
Solving the equation (26) for S, we get
C3Q
S=
(27)
C3 +C4
Substituting the equation (27) into the equation (25), we get
C3  C3 +C4  (C3 +Q)2
-C2D
0=
+
-
×
(28)
(C3 +C4 )
2
Q2
2Q2
2
-C2D
C3
C3
=
+
-
(29)
2  2(C3 +C4 )
Q2
Solving equation (29) for Q, we get
C3 +C4
2C2D
Q* =
(30)
C3
C4
60
img
Operations Research (MTH601)
61
which is the economic or optimum order quantity.
2C2D
C3
S* =
(31)
C3 +C4
C4
61
img
Operations Research (MTH601)
62
Example: The demand for an item is 18000 units/year. The cost of one purchase is Rs. 400. The holding cost is Rs.
1.2 per unit per year. The item cost is Rs. 1 per item. The shortage cost is Rs. 5 per unit per year. Determine:
(a)
The optimum order quantity.
(b)
The time between orders.
(c)
The number of orders per year.
(d)
The optimum shortages.
(e)
The maximum inventory.
(f)
The time of items being held.
(g)
The optimum annual cost.
Solution
D = 18000 units/year
or
1500 units/month
C1 = Rs. 1/item
C3 = Rs. 1.2/year/item
C2 = Rs. 400/order
C4 = Rs. 5/year/item
C3 + C4
2C D
2×400×18000
6.2
=
2
Q* =
×
a)
1.2
5
C4
C3
= 3857 Units.
t * + Q* D = 3857 1500 = 2.57 months
b)
c)
Number of orders per year = 12/2.57 = 4.66
S* =
C3 (C3 +C4 ) = 747 items
d)
2C2 D C4
= Q * -S* = 3857 - 747 = 3110 items
e)
I
max
D = 3110 / 1500 = 2.07 months
t =I
f)
1
max
g)
Annual cost = Item cost
+ Ordering cost
+ Holding cost
+ Shortage cost
Item cost = Rs. 3857 per order
Order cost = Rs. 400 per order
Rs.1.2×3110×2.07
=
Holding cost
2×12
= Rs. 322.14 per order
62
Table of Contents:
  1. Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
  2. Introduction:Model Solution, Implementation of Results
  3. Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
  4. PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
  5. PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
  6. PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
  7. PERT / CPM:Expected length of a critical path, Expected time and Critical path
  8. PERT / CPM:Expected time and Critical path
  9. PERT / CPM:RESOURCE SCHEDULING IN NETWORK
  10. PERT / CPM:Exercises
  11. Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
  12. Inventory Control:Purchasing model with shortages
  13. Inventory Control:Manufacturing model with no shortages
  14. Inventory Control:Manufacturing model with shortages
  15. Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
  16. Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
  17. Linear Programming:Formulation of the Linear Programming Problem
  18. Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
  19. Linear Programming:Model Constraints, Ingredients Mixing
  20. Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
  21. Linear Programming:LINEAR PROGRAMMING PROBLEM
  22. Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
  23. Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
  24. Linear Programming:SIMPLEX METHOD, Simplex Procedure
  25. Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
  26. Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
  27. Linear Programming:The Two Phase Method, First Iteration
  28. Linear Programming:VARIANTS OF THE SIMPLEX METHOD
  29. Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
  30. Linear Programming:Multiple or Alternative optimal Solutions
  31. Transportation Problems:TRANSPORTATION MODEL, Distribution centers
  32. Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
  33. Transportation Problems:MOVING TOWARDS OPTIMALITY
  34. Transportation Problems:DEGENERACY, Destination
  35. Transportation Problems:REVIEW QUESTIONS
  36. Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
  37. Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
  38. Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
  39. Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
  40. Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
  41. Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
  42. Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
  43. Dynamic Programming:Analysis of the Result, One Stage Problem
  44. Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
  45. Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION