 |
Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS) |
| << PERT / CPM:Exercises |
| Inventory Control:Purchasing model with shortages >> |
Operations
Research (MTH601)
51
3-5
Y
20
4
4-5
X
30
6
Resource
availability:
Number
of operators = 50
Equipments
X = 1, Y = 1, Z = 1
Segment
III: Inventory Control
Lectures
11 -16
51
Operations
Research (MTH601)
52
INVENTORY
AND CONTROL
Inventory
is the physical stock of
items held in any business
for the purpose of future
production
or
sales. In a production shop the
inventory may be in the form
of raw materials. When the
items
are
in production process, we have
the inventory as in-process
inventory and at the end of
the
production
cycle inventory is in the
form of finished goods. We
shall be dealing only with
the
finished
goods inventory. The problem
of determining inventory policies is
not a new concept
beginning.
It is only in he last two
decades that it has been
tackled with quantitative
techniques
and
mathematical models, a method amenable to
optimization.
Inventory
planning is the determination of
the type and quantity of
inventory items that would
be required at
future
points for maintaining
production schedules. Inventory
planning is generally based on
information from the
past
and
also on factors that would
arise in future. Once this
sort of planning is over,
the control process starts,
which
means
that actual and planned
inventory positions are
compared and necessary
action taken so that the
business
process
can function
efficiently.
In
inventory control, we are primarily
concerned with the inventory
cost control. The aim is
focussed to
bring
down the total inventory cost
per annum as much as
possible. Two important questions
are (1) how much
to
stock
or how much to buy and
(2) how often to buy or
when to buy. An answer to the
above questions is
usually
given
by certain mathematical models, popularly
known as `economic order
quantity models' or `economic
lot/batch
size
models (E.O.Q.).'
INVENTORY
COSTS
There
are four major elements of
inventory costs that should
be taken for analysis, such
as
Item
cost, Rs. C1/item.
(1)
(2)
Ordering
cost, Rs. C2/order.
Holding
cost Rs. C3/item/unit
time.
(3)
(4)
Shortage
cost Rs. C4/item/Unit
time.
Item
Cost (C1)
This
is the cost of the item
whether it is manufactured or purchased.
If it is manufactured, it includes
such
items
as direct material and
labour, indirect materials
and labour and overhead
expenses. When the item
is
purchased,
the item cost is the
purchase price of 1 unit.
Let it be denoted by Rs.
C1 per
item.
Purchasing
or Setup or Acquisition or Ordering
Cost (C2)
Administrative
and clerical costs are
involved in processing a purchase
order, expediting, follow up
etc., It
includes
transportation costs also.
When a unit is manufactured,
the unit set up cost
includes the cost of labour
and
materials
used in the set up and
set up testing and training
costs. This is denoted by
Rs. C2 per set up
or per order.
Inventory
holding cost (C3)
52
Operations
Research (MTH601)
53
If
the item is held in stock,
the cost involved is the
item carrying or holding
cost. Some of the costs
included
in
the unit holding cost
are
(1)
Taxes
on inventories,
(2)
Insurance
costs for inflammable and
explosive items,
(3)
Obsolescence,
(4)
Deterioration
of quality, theft, spillage
and damage to times,
(5)
Cost
of maintaining inventory
records.
This
cost is denoted by Rs.
C3/item/unit
time. The unit of time
may be days, months, weeks
or years.
Shortage
Cost (C4)
The
shortage cost is due to the
delay in satisfying demand
(due to wrong planning); but
the demand is
eventually
satisfied after a period of
time. Shortage cost is not
considered as the opportunity
cost or cost of lost
sales.
The
unit shortage cost includes
such items as,
(1)
Overtime
requirements due to
shortage,
(2)
Clerical
and administrative
expenses.
(3)
Cost
of expediting.
(4)
Loss
of goodwill of customers due to
delay.
(5)
Special
handling or packaging
costs.
(6)
Lost
production time.
This
cost is denoted by Rs.
C4 per item
per unit time of
shortage.
INVENTORY
MODELS (E.O.Q.
MODELS)
The
inventory control model can
be broadly classified into
two categories:
(1)
Deterministic inventory
problems.
(2)
Probabilistic or stochastic inventory
problems.
In
the deterministic type of
inventory control, the
parameters like demand,
ordering quantity cost, etc
are
already
known or have been
ascertained and there is no
uncertainty. In the stochastic
inventory control, the
uncertain
aspects
are taken into
account.
First
let us consider the
inventory control of the
deterministic type. There
are four EOQ models
which are
discussed
below. The first one is
the well-known Wilson's
inventory model.
Model
1: Purchasing
model with no shortages:
(Wilson's model)
The
following assumptions are
made in deriving the formula for
economic order quantity.
(1)
Demand
(D) is at a constant
rate.
(2)
Replacement
of items is instantaneous (lead
time is zero).
(3)
The
cost coefficients C1, C2,
and C3 are
constant.
There
is no shortage cost or C4 = 0.
(4)
This
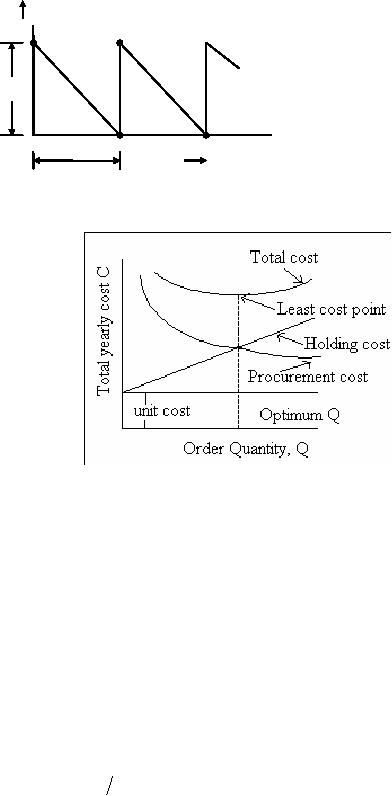
mode represented graphically in
fig. 1. This is also known
as a saw tooth model
(because of its
shape).
53
Operations
Research (MTH601)
54
Quantity
Q
=Im
t
Time
Fig.
1
Fig.
2
In
this model, at time
t
= 0, we order a
quantity Q
which is
stored as maximum inventory,
1m. The time
`t' denotes
the
time
of one period or it is the
time between orders or it is
the cycle time. During
this time, the items
are depleting and
reaching
a zero value at the end of
time t.
At time t
another
order of the same quantity
is to be placed to bring
the
stock
upto Q
again and
the cycle is repeated. Hence
this is a fixed order
quantity model.
The
total cost for this
model for one cycle is
made up of three cost
components.
Total
cost/period = (Item cost +
set up cost + holding
cost/period)
Item
cost per period = (Cost of
item) �
(number
of items ordered/period)
=
C1Q
(1)
Purchase
or set up cost per period =
C2 (only one
set up per period)
Item
holding cost per period =
(Holding cost) �
(average
inventory per period) �
(time
per period)
=
C3 Q
2
�
t
(2)
54
Operations
Research (MTH601)
55
Therefore
the total cost per
period (C ′) =
C
Q +
C
+
C
Q 2 �
t
(3)
1
2
3
But
the time for one
period t
=
Q
D
(4)
Therefore
the total cost per
unit time, C
=
C′
t
(5)
D
Q
C
+
C1D
+
C2
+C
(6)
3 2
Q
Substituting
the value of t,
we get C
=
C
D +
C
D Q +
C
Q 2
(7)
1
2
3
The
cost components of the above
equations can be represented as
shown in fig 2 and an
optimum order quantity
for
one
period is found when
Purchase
cost = Item holding
cost.
C2D
C3Q
=
Q
2
2C2D
2C2D
Q2 =
Q*
=
(8)
C3
C3
This
minimum inventory cost per
unit time can also be
found by differentiating C
with
respect to Q
and
equating it to
zero.
The derivative of the
equation is,
C3
dC
-C2 D
+
=0
=
(9)
dQ
Q
2
2
Solving
for Q,
we get
2C2D
Q*
=
(10)
C3
This
value of Q*
is the
economic order quantity and
any other order quantity
will result in a higher
cost.
The
corresponding period t*
is found
from
t*
=
Q*
D
(11)
The
optimum number of orders per
year is determined
from
N
*
=
D
Q*
where
D
is the
demand per year.
55
Operations
Research (MTH601)
56
56

Operations
Research (MTH601)
57
Example
1: The
demand rate for a particular
item is 12000 units/year.
The ordering cost is Rs.
100 per order
and
the
holding cost is Rs. 0.80
per item per month. If no
shortages are allowed and
the replacement is
instantaneous,
determine:
(1)
The
economic order
quantity.
(2)
The
time between orders.
(3)
The
number of orders per
year.
(4)
The
optimum annual cost if the
cost of item is Rs. 2 per
item.
Solution:
Note
that the holding cost is given
per month and convert the same
into cost per
year.
C1 = Rs.
2/item
C2 = Rs.
100/order
C3 = Rs.
0.80/item/month
=
Rs. 9.6/item/year
D
= 12000
items/year
a)
The
economic order
quantity
2C2 D
Q*
=
C3
2�100�12000
=
9.6
=
500
units
b)
The
time between orders
t*
=
Q*
D
=
500 /
12000 yr.
=
500
1000 month
=
0.5
month
c)
The
number of orders/year
N
=
D
Q*
=
12000
/ 500 =
24
d)
The
optimum annual cost
57
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION