 |
PERT / CPM:Exercises |
| << PERT / CPM:RESOURCE SCHEDULING IN NETWORK |
| Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS) >> |
Operations
Research (MTH601)
50
which
are to be postponed. The
slack is usually the basis
on which priority is accorded to
various job. Hence,
the
jobs,
which are most critical,
will be scheduled
first.
In
any problem on resource
allocation, the following
three rules may be
applied.
(i)
The resources are to be
allocated in the order of
time i.e. start on the
first day and schedule
all possible jobs
then
the second day
etc.
(ii)
When several jobs compete
for the same resources
preference should be given to
the job with least
slack.
(iii)
The non-critical jobs should be
rescheduled so that resources
would be free for scheduling
the critical jobs.
Exercises
1.
Following
are the manpower
requirements for each
activity in a project.
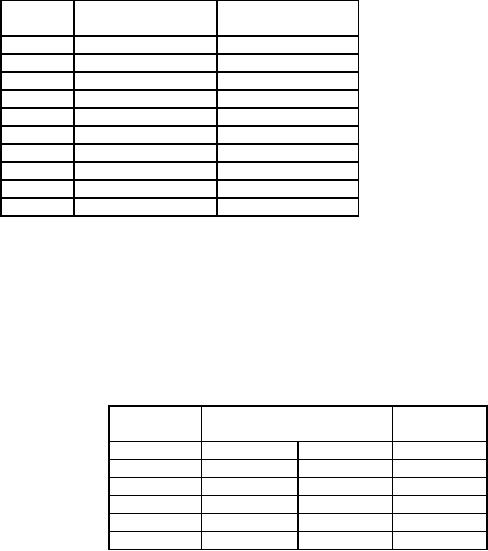
Activity
Normal
Time (days)
Manpower
required
per
day
1-2
10
2
1-3
11
3
2-4
13
4
2-6
14
3
3-4
10
1
4-5
7
3
4-6
17
5
5-7
13
3
6-7
9
8
7-8
1
11
(i)
Draw
the network and find 'total
float' and 'free float' for
each activity.
(ii)
The
contractor stipulates that
during the first 26 days
only 4 to 5 men and during
the remaining days
8
to 11 men only can made be
available. Rearrange the activities
for leveling the
manpower
resources
satisfying the above condition.
2.
For
a project consisting of several
activities, the duration and
required resources for
carrying out each of
the
activities and their availabilities are
given below. Find the
project completion time under
the given
resource
constraints.
Activity
Resources
Required
Duration
Equipment
Operators
(days)
1-2
X
30
4
1-3
Y
20
3
1-4
Z
20
6
2-4
X
30
4
2-5
Z
20
8
3-4
Y
20
4
50
Table of Contents:
- Introduction:OR APPROACH TO PROBLEM SOLVING, Observation
- Introduction:Model Solution, Implementation of Results
- Introduction:USES OF OPERATIONS RESEARCH, Marketing, Personnel
- PERT / CPM:CONCEPT OF NETWORK, RULES FOR CONSTRUCTION OF NETWORK
- PERT / CPM:DUMMY ACTIVITIES, TO FIND THE CRITICAL PATH
- PERT / CPM:ALGORITHM FOR CRITICAL PATH, Free Slack
- PERT / CPM:Expected length of a critical path, Expected time and Critical path
- PERT / CPM:Expected time and Critical path
- PERT / CPM:RESOURCE SCHEDULING IN NETWORK
- PERT / CPM:Exercises
- Inventory Control:INVENTORY COSTS, INVENTORY MODELS (E.O.Q. MODELS)
- Inventory Control:Purchasing model with shortages
- Inventory Control:Manufacturing model with no shortages
- Inventory Control:Manufacturing model with shortages
- Inventory Control:ORDER QUANTITY WITH PRICE-BREAK
- Inventory Control:SOME DEFINITIONS, Computation of Safety Stock
- Linear Programming:Formulation of the Linear Programming Problem
- Linear Programming:Formulation of the Linear Programming Problem, Decision Variables
- Linear Programming:Model Constraints, Ingredients Mixing
- Linear Programming:VITAMIN CONTRIBUTION, Decision Variables
- Linear Programming:LINEAR PROGRAMMING PROBLEM
- Linear Programming:LIMITATIONS OF LINEAR PROGRAMMING
- Linear Programming:SOLUTION TO LINEAR PROGRAMMING PROBLEMS
- Linear Programming:SIMPLEX METHOD, Simplex Procedure
- Linear Programming:PRESENTATION IN TABULAR FORM - (SIMPLEX TABLE)
- Linear Programming:ARTIFICIAL VARIABLE TECHNIQUE
- Linear Programming:The Two Phase Method, First Iteration
- Linear Programming:VARIANTS OF THE SIMPLEX METHOD
- Linear Programming:Tie for the Leaving Basic Variable (Degeneracy)
- Linear Programming:Multiple or Alternative optimal Solutions
- Transportation Problems:TRANSPORTATION MODEL, Distribution centers
- Transportation Problems:FINDING AN INITIAL BASIC FEASIBLE SOLUTION
- Transportation Problems:MOVING TOWARDS OPTIMALITY
- Transportation Problems:DEGENERACY, Destination
- Transportation Problems:REVIEW QUESTIONS
- Assignment Problems:MATHEMATICAL FORMULATION OF THE PROBLEM
- Assignment Problems:SOLUTION OF AN ASSIGNMENT PROBLEM
- Queuing Theory:DEFINITION OF TERMS IN QUEUEING MODEL
- Queuing Theory:SINGLE-CHANNEL INFINITE-POPULATION MODEL
- Replacement Models:REPLACEMENT OF ITEMS WITH GRADUAL DETERIORATION
- Replacement Models:ITEMS DETERIORATING WITH TIME VALUE OF MONEY
- Dynamic Programming:FEATURES CHARECTERIZING DYNAMIC PROGRAMMING PROBLEMS
- Dynamic Programming:Analysis of the Result, One Stage Problem
- Miscellaneous:SEQUENCING, PROCESSING n JOBS THROUGH TWO MACHINES
- Miscellaneous:METHODS OF INTEGER PROGRAMMING SOLUTION