 |
BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS |
| << BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT |
| BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION >> |

MTH001
Elementary Mathematics
LECTURE #
6
A
well defined collection of
{distinct}objects is called a
set.
The
objects are called the
elements or members of the
set.
Sets
are denoted by capital
letters A, B, C ..., X, Y, Z.
The
elements of a set are
represented by lower case
letters
a,
b, c, ... , x, y, z.
If
an object x is a member of a set A we
write x ∈A, which
reads "x
belongs
to A" or "x is in A" or "x is an element of
A",
otherwise
we
write
x ∉A,
which reads "x does not
belong to A" or "x is not in A" or "x is
not
an
element of A".
TABULAR
FORM
Listing
all the elements of a set,
separated by commas and
enclosed within
braces
or
curly brackets{}.
EXAMPLES
In
the following examples we
write the sets in Tabular
Form.
A
= {1, 2, 3, 4, 5}
is
the set of first five
Natural
Numbers.
B
= {2, 4, 6, 8, ..., 50} is the
set of Even
numbers up to
50.
C
= {1, 3, 5, 7, 9 ...} is the set of
positive
odd numbers.
NOTE
The
symbol "..." is called an ellipsis. It is
a
short
for "and so forth."
DESCRIPTIVE
FORM:
Stating
in words the elements of a
set.
EXAMPLES
Now
we will write the same
examples which we write in
Tabular
Form
,in the Descriptive
Form.
A
= set of first five Natural
Numbers.( is the Descriptive
Form )
B
= set of positive even
integers less or equal to
fifty.
(
is the Descriptive Form
)
C
= {1, 3, 5, 7, 9, ...}
(
is the Descriptive Form
)
C
= set of positive odd
integers.
(
is the Descriptive Form
)
SET
BUILDER FORM:
Writing
in symbolic form the common
characteristics shared by all
the
elements
of the set.
EXAMPLES:
Now
we will write the same
examples which we write in
Tabular as well as Descriptive
Form
,in
Set Builder Form .
A
= {x �N / x<=5} ( is the Set
Builder Form)
B
= {x � E / 0 < x <=50} ( is the Set
Builder Form)
C
= {x �O / 0 < x } ( is the Set Builder
Form)
SETS
OF NUMBERS:
1.
Set of Natural
Numbers
N
= {1, 2, 3, ... }
2.
Set of Whole
Numbers
W
= {0, 1, 2, 3, ... }
Page
21

MTH001
Elementary Mathematics
3.
Set of Integers
Z
= {..., -3, -2, -1, 0, +1,
+2, +3, ...}
=
{0, �1, �2, �3, ...}
{"Z"
stands for the first
letter of the German word
for integer: Zahlen.}
4.
Set of Even
Integers
E
= {0, �
2, � 4, �
6,
...}
5.
Set of Odd
Integers
O
= {�
1, � 3, �
5,
...}
6.
Set of Prime
Numbers
P
= {2, 3, 5, 7, 11, 13, 17,
19, ...}
7.
Set of Rational Numbers (or
Quotient of Integers)
Q
= {x | x = ; p, q ∈Z, q ≠
0}
8.
Set of Irrational
Numbers
Q
= Q′
= { x | x is
not rational}
For
example, √2, √3, �, e,
etc.
9.
Set of Real
Numbers
R
= Q ∪
Q′
10.
Set of Complex
Numbers
C
= {z | z = x + iy;
x, y ∈
R}
SUBSET:
If
A & B are two sets, A is
called a subset of B, written A
⊆
B,
if, and only if,
any
element
of A is also an element of B.
Symbolically:
A
⊆
B ⇔ if x ∈
A
then x ∈
B
REMARK:
1.
When A ⊆
B,
then B is called a superset of
A.
2.
When A is not subset of B,
then there exist at least
one x ∈
A
such
that
x ∉B.
3.
Every set is a subset of
itself.
EXAMPLES:
Let
A
= {1, 3, 5}
B
= {1, 2, 3, 4, 5}
C
= {1, 2, 3, 4} D = {3, 1, 5}
Then
A
⊆
B (
Because every element of A is in B
)
C
⊆
B (
Because every element of C is
also an element of B )
A
⊆
D (
Because every element of A is
also an element of D and
also note
that
every element of D is in A so D ⊆
A
)
and
A is not subset of C .
(
Because there is an element 5 of A
which is not in C )
EXAMPLE:
The
set of integers "Z" is a
subset of the set of
Rational Number
"Q",
since every integer `n'
could be written as:
n
n=
∈Q
1
Hence
Z ⊆
Q.
PROPER
SUBSET
Let
A and B be sets. A is a proper
subset of B, if, and only
if, every element of A
is
in
B but there is at least one
element of B that is not in A,
and is denoted as A ⊂
B.
Page
22

MTH001
Elementary Mathematics
EXAMPLE:
Let
A = {1, 3, 5}
B
= {1, 2, 3, 5}
then
A ⊂
B (
Because there is an element 2 of B
which is not in A).
EQUAL
SETS:
Two
sets A and B are equal
if, and only if,
every element of A is in B and
every
element
of B is in A and is denoted A = B.
Symbolically:
A
= B iff A ⊆
B
and B ⊆
A
EXAMPLE:
Let
A = {1, 2, 3, 6}
B
= the set of positive
divisors of 6
C
= {3, 1, 6, 2} D = {1, 2, 2, 3, 6, 6,
6}
Then
A, B, C, and D are all equal
sets.
NULL
SET:
A
set which contains no
element is called a null
set, or an
empty
set or a
It
is denoted by the Greek
letter ∅
(phi) or {
}.
void
set.
EXAMPLE
A
= {x | x is a person taller than 10
feet} = ∅
(
Because there does
not
exist any human being
which is taller then 10 feet
)
B
= {x | x2 = 4, x is odd} = ∅
(Because we
know that there does
not exist any
odd
whose square is 4)
REMARK
∅
is
regarded as a subset of every
set.
EXERCISE:
Determine
whether each of the
following statements is true or
false.
a.
x ∈
{x}
TRUE
(
Because x is the member of
the singleton set { x }
)
a.
{x}⊆ {x}
TRUE
(
Because Every set is the
subset of itself.
Note
that
every Set has necessarily
tow subsets ∅
and
the Set itself, these
two
subset
are known as Improper
subsets and any other
subset is called
Proper
Subset)
a.
{x} ∈{x}
FALSE
(
Because { x} is not the
member of {x} ) Similarly
other
{x}
∈{{x}}
d.
TRUE
∅
⊆ {x}
e.
TRUE
∅
∈ {x}
f.
FALSE
UNIVERSAL
SET:
The
set of all elements under
consideration is called the
Universal Set.
The
Universal Set is usually
denoted by U.
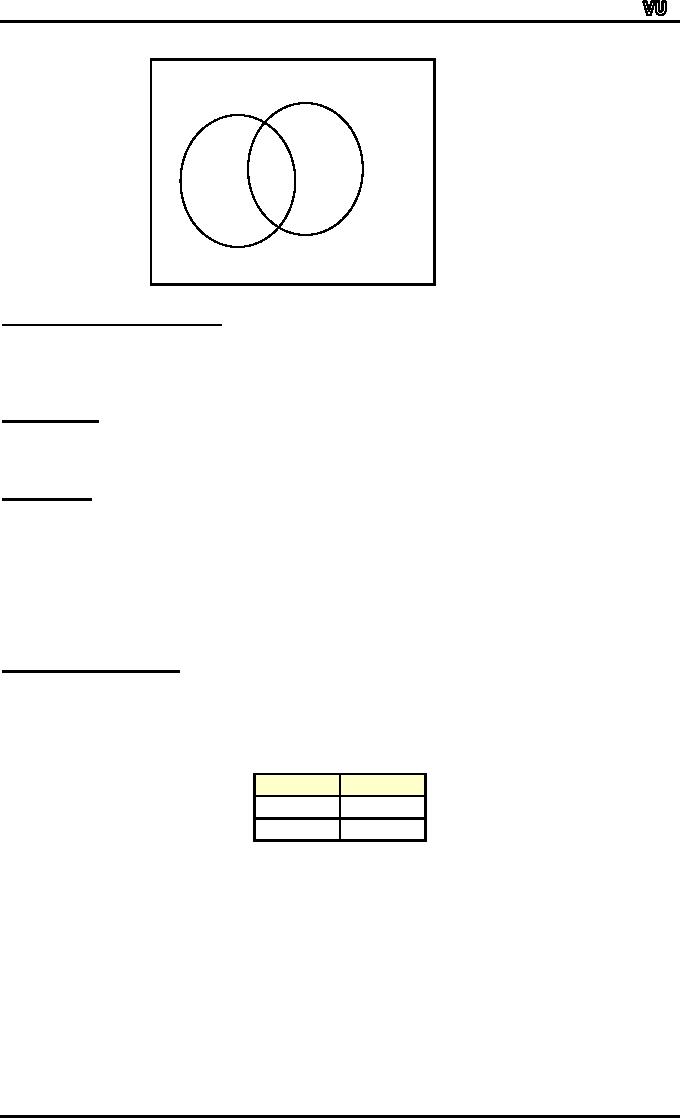
VENN
DIAGRAM:
A
Venn diagram is a graphical
representation of sets by regions in
the plane.
The
Universal Set is represented by
the interior of a rectangle,
and the other
sets
are
represented by disks lying
within the rectangle.
Page
23
MTH001
Elementary Mathematics
U
A
A
B
FINITE
AND INFINITE SETS:
A
set S
is said to be
finite
if it contains
exactly m
distinct
elements where m
denotes
some non negative
integer.
In
such case we write |S|
=
m
or n(S) =
m
A
set is said to be infinite
if it is not
finite.
EXAMPLES:
1.
The set S of letters of
English alphabets is finite
and |S|
=
26
2.
The null set ∅
has
no elements, is finite and |∅|
=
0
3.
The set of positive integers
{1, 2, 3,...} is infinite.
EXERCISE:
Determine
which of the following sets
are finite/infinite.
1.
A = {month in
the year}
FINITE
2.
B = {even
integers}
INFINITE
3.
C = {positive
integers less than 1}
FINITE
4.
D = {animals
living on the earth}
FINITE
5.
E = {lines
parallel to x-axis}
INFINITE
6.
F = {x ∈R | x100 + 29x50
1 =
0}
FINITE
7.
G = {circles
through origin}
INFINITE
MEMBERSHIP
TABLE:
A
table displaying the
membership of elements in sets. To
indicate that
an
element is in a set, a 1 is used; to
indicate that an element is
not in a set, a 0 is
used.
Membership
tables can be used to prove
set identities.
Ac
A
1
0
0
1
The
above table is the Member
ship table for Complement of
A. now in the
above
table note that if an
element is the member of A
then it can`t be the
member
of
Ac thus
where in the table we have 1
for A in that row we have 0
in Ac.
Page
24
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS