 |
BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT |
| << BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL |
| BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS >> |
MTH001
Elementary Mathematics
LECTURE #
5
EXAMPLE
An
interesting teacher keeps me
awake. I stay awake in
Discrete Mathematics
class.
Therefore, my
Discrete Mathematics teacher is
interesting.
Is
the above argument
valid?
ARGUMENT:
An
argument
is
a list of statements called
premises
(or
assumptions
or
hypotheses)
followed by a
statement called the
conclusion.
P1
Premise
P2
Premise
P3
Premise
.
. . . .. . . . .
Pn
Premise
______________
∴C
Conclusion
NOTE
The
symbol \
read
"therefore," is normally placed
just before the
conclusion.
VALID
AND INVALID ARGUMENT:
An
argument is valid
if the
conclusion is true when all
the premises are
true.
Alternatively,
an argument is valid if conjunction of
its premises imply
conclusion.That is
(P1∧ P2 ∧
P3 ∧ . . . ∧
Pn)
→
C is a
tautology.
An
argument is invalid
if the
conclusion is false when all
the premises are
true.
Alternatively,
an argument is invalid if conjunction of
its premises does not
imply conclusion.
EXAMPLE:
Show
that the following argument
form is valid:
p→q
p
∴ q
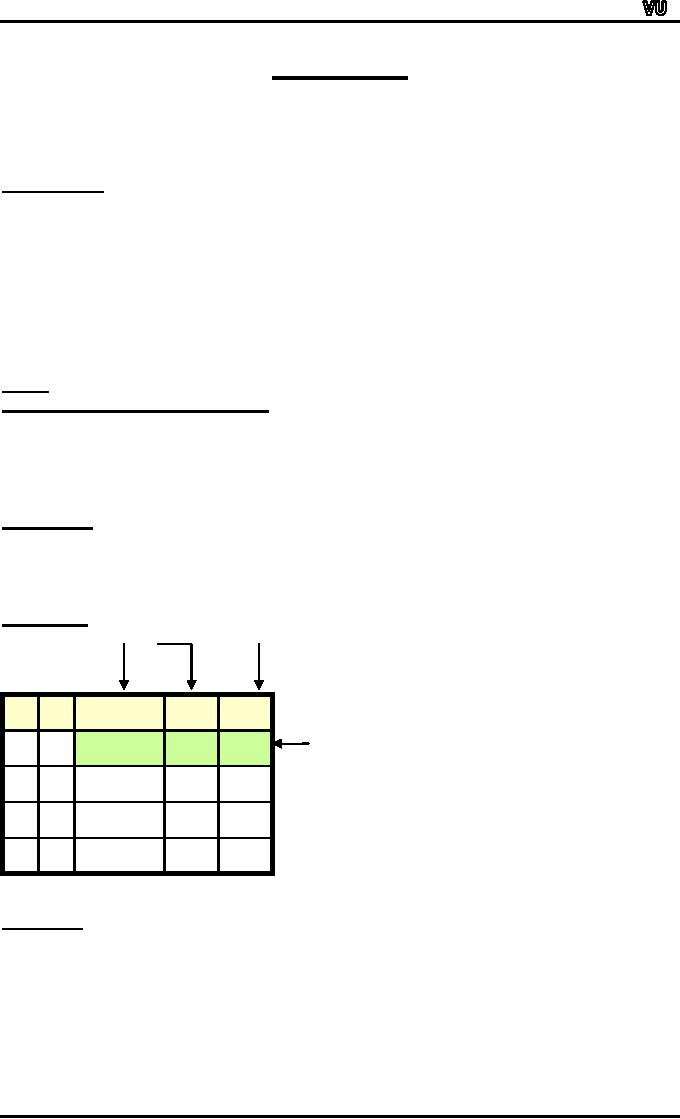
SOLUTION
premises
conclusion
p→q
p
q
p
q
critical
row
T
T
T
T
T
T
F
F
T
F
F
T
T
F
T
F
F
T
F
F
EXAMPLE
Show
that the following argument
form is invalid:
p→q
q
∴ p
Page
19
MTH001
Elementary Mathematics
SOLUTION
premises
conclusion
p→q
p
q
q
p
T
T
T
T
T
T
F
F
F
T
critical
row
F
T
T
T
F
F
F
T
F
F
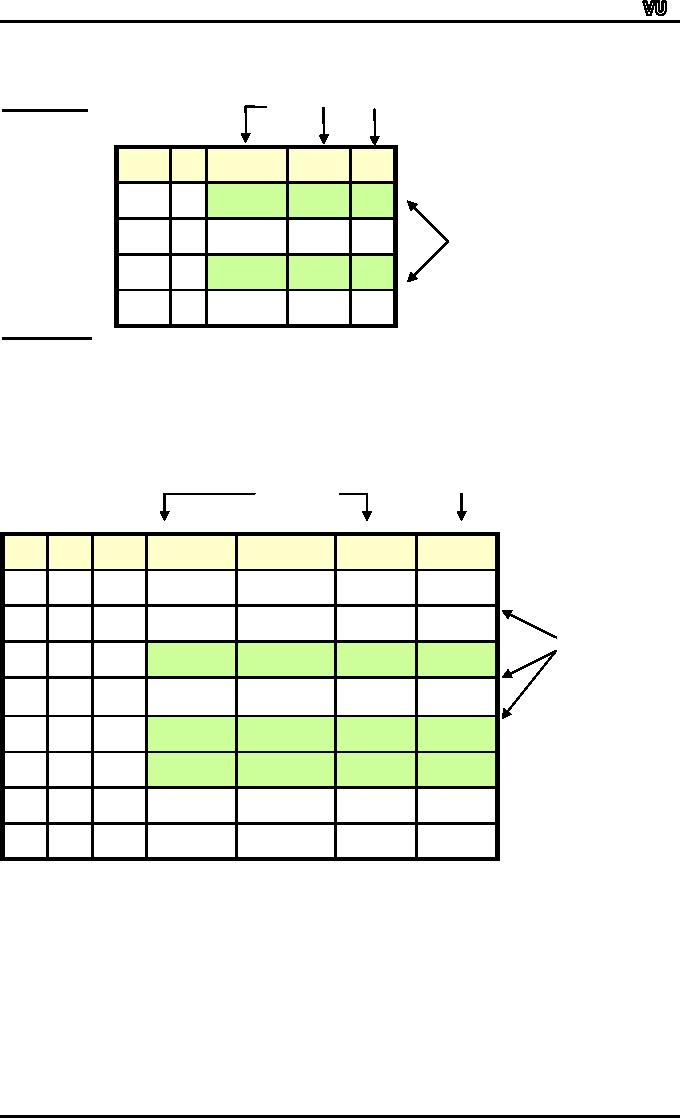
EXERCISE:
Use
truth table to determine the
argument form
p∨q
p
→
~q
p→r
∴ r
is
valid or invalid.
premises
conclusion
p∨q
p→~q
p→r
p
q
r
r
T
T
T
T
F
T
T
T
T
F
T
F
F
F
critical
rows
T
F
T
T
T
T
T
T
F
F
T
T
F
F
F
T
T
T
T
T
T
F
T
F
T
T
T
F
F
F
T
F
T
T
T
F
F
F
F
T
T
F
The
argument form is
invalid
Page
20
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS