 |
BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL |
| << APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS |
| BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT >> |
MTH001
Elementary Mathematics
LECTURE #
4
BICONDITIONAL
If p
and q are statement
variables, the biconditional of p
and q is
"p
if, and only if,
q" and is
denoted p↔q. if and
only if abbreviated
iff.
The
double headed arrow " ↔" is the
biconditional
operator.
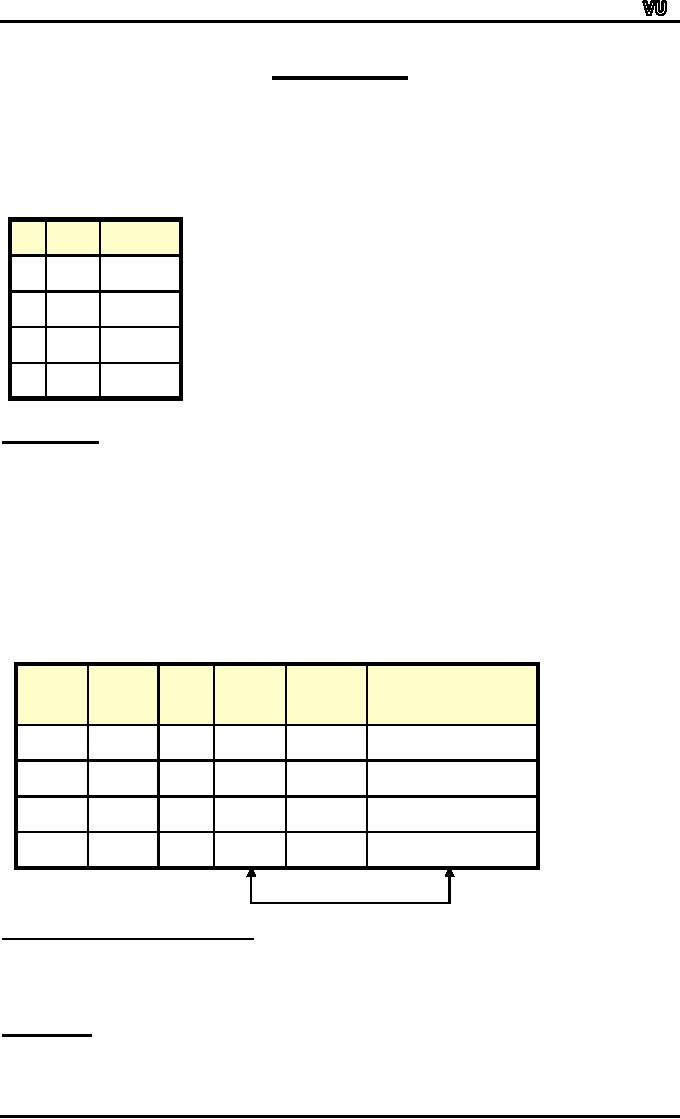
TRUTH
TABLE FOR
p↔q.
p
↔q
p
q
T
T
T
T
F
F
F
T
F
F
F
T
EXAMPLES:
True
or false?
1."1+1 = 3
if and
only if earth
is flat"
TRUE
2.
"Sky is
blue iff
1 =
0"
FALSE3.
"Milk is
white iff
birds
lay eggs"
TRUE
4.
"33 is
divisible by 4 if and
only if horse
has four legs"
FALSE
5.
"x >
5 iff x2 > 25"
FALSE
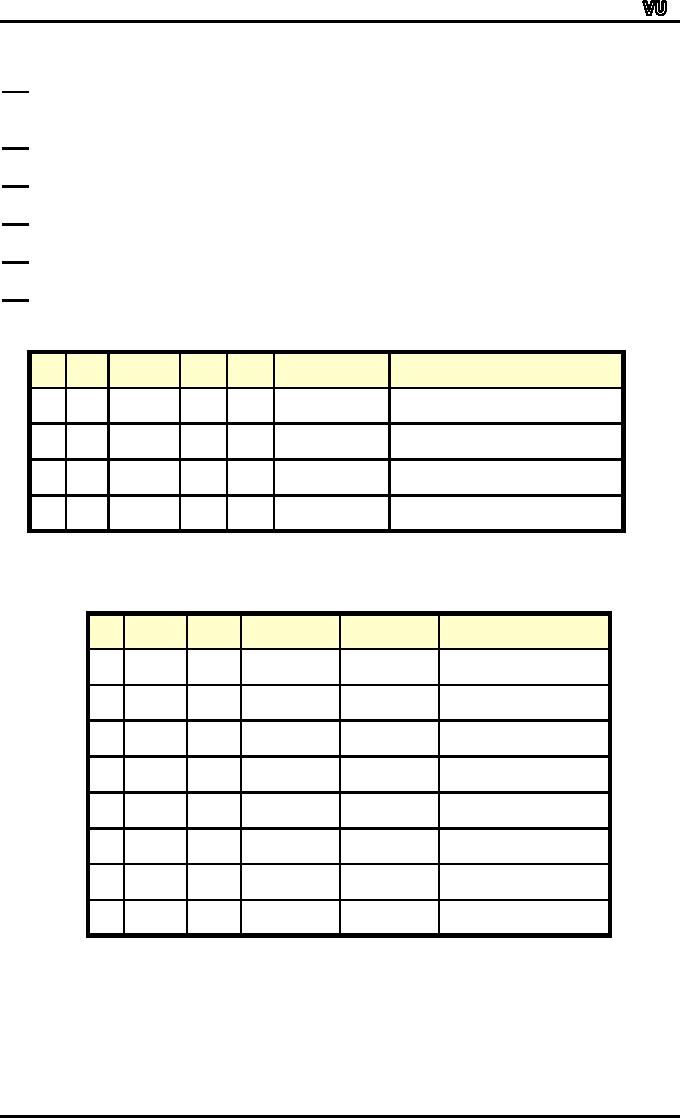
p↔q
≡
(p→q)∧(q→p)
p↔q
p→q
q→p
(p→q)∧(q→p)
p
q
T
T
T
T
T
T
T
F
F
F
T
F
F
T
F
T
F
F
F
F
T
T
T
T
same
truth values
REPHRASING
BICONDITIONAL:
p↔q is also
expressed as:
"p
is necessary and sufficient
for q"
"if
p then q, and
conversely"
"p
is equivalent to q"
EXERCISE:
Rephrase
the following propositions in
the form "p if and only if
q" in English.
1.If
it is hot outside you buy an ice
cream cone, and if you buy an
ice cream
Page
15
MTH001
Elementary Mathematics
cone
it is hot outside.
Sol
You
buy an ice cream cone if
and only if it is hot
outside.
2.For
you to win the contest it is
necessary and sufficient
that you have
the
only
winning ticket.
Sol
You win
the contest if and only if
you hold the only
winning ticket.
3.If
you read the news
paper every day, you will be
informed and
conversely.
Sol
You will be
informed if and only if you
read the news paper
every day.4.It
rains if it is a
weekend
day, and it is a weekend day if it
rains.
Sol
It rains if
and only if it is a weekend
day.
5.The
train runs late on exactly
those days when I take
it.
Sol
The
train runs late if and
only if it is a day I take
the train.
6.This
number is divisible by 6 precisely
when it is divisible by both 2
and 3.
Sol
This
number is divisible by 6 if and
only if it is divisible by both 2
and 3.
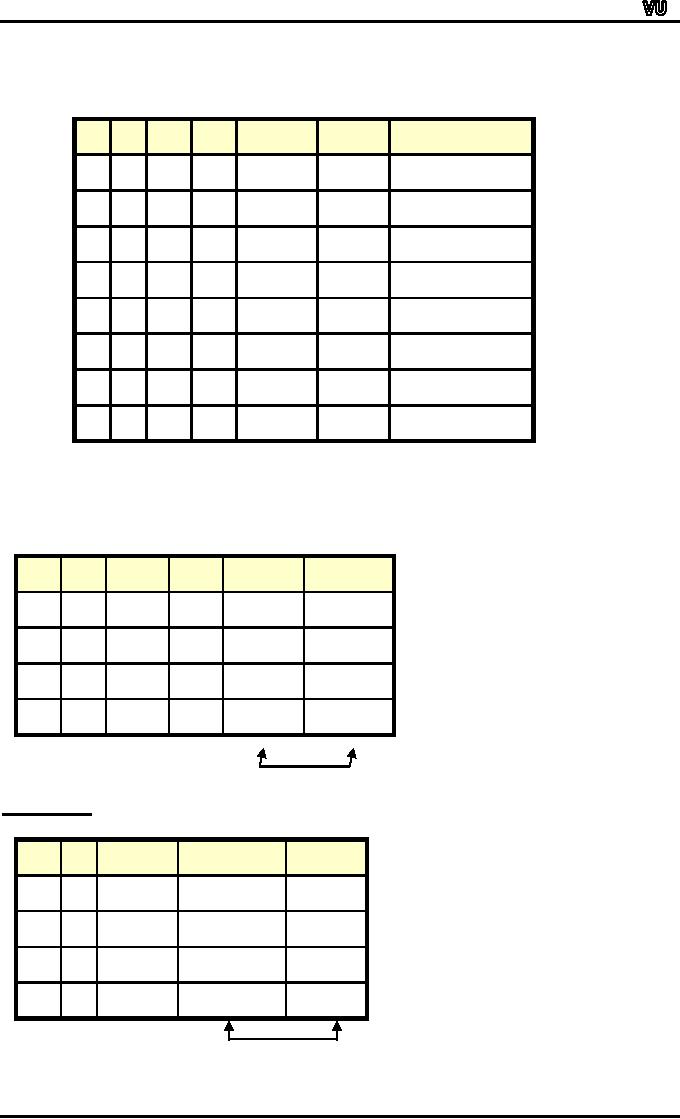
TRUTH
TABLE FOR
(p→q) ↔
(~
q→
~
p)
p→q
~
q→
~
p
(p→q)
↔
(~ q→ ~ p)
p
q
~q
~p
T
T
T
F
F
T
T
T
F
F
T
F
F
T
F
T
T
F
T
T
T
F
F
T
T
T
T
T
TRUTH
TABLE FOR
(p↔q)↔(r↔q)
p↔q
r↔q
(p↔q)↔(r↔q)
p
q
r
T
T
T
T
T
T
T
T
F
T
F
F
T
F
T
F
F
T
T
F
F
F
T
F
F
T
T
F
T
F
F
T
F
F
F
T
F
F
T
T
F
F
F
F
F
T
T
T
TRUTH
TABLE FOR
p
∧
~r
↔q∨r
Here
p ∧
~ r ↔q
∨
r
means (p ∧
(~
r)) ↔(q ∨
r)
Page
16
MTH001
Elementary Mathematics
p∧~r
q∨r
p
∧
~r ↔q∨r
p
q
r
~r
T
T
T
F
F
T
F
T
T
F
T
T
T
T
T
F
T
F
F
T
F
T
F
F
T
T
F
F
F
T
T
F
F
T
F
F
T
F
T
F
T
F
F
F
T
F
F
T
F
F
F
F
T
F
F
T
LOGICAL
EQUIVALENCE
INVOLVING
BICONDITIONAL
Show
that ~p↔q and
p↔~q are
logically equivalent
~p↔q
p↔~q
p
q
~p
~q
T
T
F
F
F
F
T
F
F
T
T
T
F
T
T
F
T
T
F
F
T
T
F
F
same
truth values
EXERCISE:
Show
that ~(p⊕q) and
p↔q are
logically equivalent
p⊕q
~(p⊕q)
p↔q
p
q
T
T
F
T
T
T
F
T
F
F
F
T
T
F
F
F
F
F
T
T
same
truth values
Page
17

MTH001
Elementary Mathematics
LAWS
OF LOGIC:
p↔q≡q↔p
1.Commutative
Law:
p
→q
≡
~p ∨ q
2.Implication
Laws:
≡
~(p
∧
~q)
(p
∧
q)→r
≡
p →(q
→r)
3.Exportation
Law:
p
↔
q ≡ (p →q)∧(q →p)
4.Equivalence:
p
→q
≡
(p ∧ ~q) →c
5.Reductio
ad absurdum
APPLICATION:
Rewrite
the statement forms without
using the symbols →
or
↔
1.p∧~q→r
2.
(p→r)↔(q →r)
SOLUTION
1.p∧~q→r
≡
(p∧~q)→r
order
of operations
≡~(p∧~q)
∨
r
implication
law
2.(p→r)↔(q
→r)
≡
(~p
∨
r)↔(~q
∨
r)
implication law
≡
[(~p
∨
r) →(~q
∨
r)]
∧
[(~q
∨
r) →(~p
∨
r)]
equivalence
of biconditional
≡
[~(~p
∨
r) ∨ (~q ∨ r)] ∧ [~(~q
∨
r) ∨ (~p ∨ r)]
implication
law
Rewrite
the statement form ~p ∨
q
→
r
∨
~q
to a logically
equivalent form that
uses
only
~
and ∧
SOLUTION
STATEMENT
REASON
~p
∨
q → r ∨
~q
Given
statement form
≡
(~p
∨
q) → (r ∨
~q)
Order
of operations
≡
~[(~p
∨
q) ∧ ~ (r ∨
~q)]
Implication
law p→q ≡
~(p∧~
q)
≡
~[~(p
∧
~q)
∧
(~r
∧
q)]
De
Morgan's law
Show
that ~(p→q) →
p
is a tautology
without using truth
tables.
SOLUTIONSTATEMENT
REASON
~(p→q)
→
p
Given
statement form
≡
~[~(p
∧
~q)]
→
p
Implication
law p→q ≡
~(p
∧
~q)
≡
(p ∧ ~q) → p
Double
negation law
≡
~(p
∧
~q)
∨
p
Implication
law p→q ≡
~p ∨ q
≡
(~p
∨
q) ∨ p
De
Morgan's law
≡
(q ∨ ~p) ∨ p
Commutative
law of
∨≡
q ∨ (~p ∨ p)
Associative
law of
∨≡
q ∨ t
Negation
law
≡t
Universal
bound law
EXERCISE:
Suppose
that p and q are statements
so that p→q is
false.
Find
the truth values
of
each of the
following:
1.~
p →
q
2.p
∨
q
3.q
↔
p
SOLUTION
1.TRUE
2.TRUE
3.FALSE
Page
18
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS