APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS

<< Truth Tables for:DE MORGANâ€™S LAWS, TAUTOLOGY

BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL >>

MTH001 Elementary Mathematics

LECTURE # 3

APPLYING LAWS OF LOGIC

Using law of logic, simplify the statement form

p ∨ [~(~p ∧ q)]

Solution:

p ∨ [~(~p ∧ q)] ≡ p ∨ [~(~p) ∨ (~q)]

DeMorgan's Law

≡p ∨ [p∨(~q)]

Double Negative Law

≡ [p ∨ p]∨(~q)

Associative Law for ∨

≡p ∨ (~q)

Indempotent Law

Which is the simplified statement form.

EXAMPLE Using Laws of Logic, verify the logical equivalence

~ (~ p ∧ q) ∧ (p ∨ q) ≡p

~(~p ∧ q) ∧ (p∨q) ≡ (~(~p) ∨ ~q) ∧(p ∨ q)

DeMorgan's Law

≡ (p ∨ ~q) ∧ (p∨q)

Double Negative Law

≡ p ∨ (~q ∧ q)

Distributive Law

≡p∨c

Negation Law

≡p

Identity Law

SIMPLIFYING A STATEMENT:

"You will get an A if you are hardworking and the sun shines, or you are hardworking and it

rains."

Rephrase the condition more simply.

Solution:

Let

p = "You are hardworking'

q = "The sun shines"

r = "It rains" .The condition is then (p ∧ q) ∨ (p ∧ r)

And using distributive law in reverse,

(p ∧ q) ∨ (p ∧ r) ≡ p ∧ (q ∨ r)

Putting p ∧ (q ∨ r) back into English, we can rephrase the given sentence as

"You will get an A if you are hardworking and the sun shines or it rains.

EXERCISE:

Use Logical Equivalence to rewrite each of the following sentences more simply.

1.It is not true that I am tired and you are smart.

{I am not tired or you are not smart.}

2.It is not true that I am tired or you are smart.

{I am not tired and you are not smart.}

3.I forgot my pen or my bag and I forgot my pen or my glasses.

{I forgot my pen or I forgot my bag and glasses.

4.It is raining and I have forgotten my umbrella, or it is raining and I have

forgotten my hat.

{It is raining and I have forgotten my umbrella or my hat.}

CONDITIONAL STATEMENTS:

Introduction

Consider the statement:

"If you earn an A in Math, then I'll buy you a computer."

This statement is made up of two simpler statements:

p: "You earn an A in Math," and

q: "I will buy you a computer."

The original statement is then saying :

if p is true, then q is true, or, more simply, if p, then q.

We can also phrase this as p implies q, and we write p → q.

CONDITIONAL STATEMENTS OR IMPLICATIONS:

Page 9

MTH001 Elementary Mathematics

If p and q are statement variables, the conditional of q by p is "If p then q"

or "p implies q" and is denoted p → q.

It is false when p is true and q is false; otherwise it is true. The arrow "→ " is the conditional

operator, and in p → q the statement p is called

the hypothesis (or antecedent) and q is called the conclusion (or consequent).

TRUTH TABLE:

p→q

PRACTICE WITH CONDITIONAL STATEMENTS:

Determine the truth value of each of the following conditional statements:

1. "If 1 = 1, then 3 = 3."

TRUE

2. "If 1 = 1, then 2 = 3."

FALSE

3. "If 1 = 0, then 3 = 3."

TRUE

4. "If 1 = 2, then 2 = 3."

TRUE

5. "If 1 = 1,then 1 = 2 and 2 = 3."

FALSE

6. "If 1 = 3 or 1 = 2 then 3 = 3."

TRUE

ALTERNATIVE WAYS OF EXPRESSING IMPLICATIONS:

The implication p → q could be expressed in many alternative ways as:

·"if p then q"

·"not p unless q"

·"p implies q"

·"q follows from p"

·"if p, q"

·"q if p"

·"p only if q"

·"q whenever p"

·"p is sufficient for q"

·"q is necessary for p"

EXERCISE:

Write the following statements in the form "if p, then q" in English.

a)Your guarantee is good only if you bought your CD less than 90 days ago.

If your guarantee is good, then you must have bought your CD player less

than 90 days ago.

b)To get tenure as a professor, it is sufficient to be world-famous.

If you are world-famous, then you will get tenure as a professor.

c)That you get the job implies that you have the best credentials.

If you get the job, then you have the best credentials.

d)It is necessary to walk 8 miles to get to the top of the Peak.

If you get to the top of the peak, then you must have walked 8 miles.

TRANSLATING ENGLISH SENTENCES TO SYMBOLS:

Let p and q be propositions:

p = "you get an A on the final exam"

q = "you do every exercise in this book"

r = "you get an A in this class"

Write the following propositions using p, q,and r and logical connectives.

1.To get an A in this class it is necessary for you to get an A on the final.

p→r

SOLUTION

2.You do every exercise in this book; You get an A on the final, implies,

you get an A in the class.

Page 10

MTH001 Elementary Mathematics

p∧q→r

SOLUTION

3. Getting an A on the final and doing every exercise in this book is sufficient

For getting an A in this class.

p∧q→r

SOLUTION

TRANSLATING SYMBOLIC PROPOSITIONS TO ENGLISH:

Let p, q, and r be the propositions:

p = "you have the flu"

q = "you miss the final exam"

r = "you pass the course"

Express the following propositions as an English sentence.

1.p → q

If you have flu, then you will miss the final exam.2.~q → r

If you don't miss the final exam, you will pass the course.3.~p ∧ ~q→ r

If you neither have flu nor miss the final exam, then you will pass the course.

HIERARCHY OF OPERATIONS

FOR LOGICAL CONNECTIVES

·~

(negation)

·∧ (conjunction), ∨ (disjunction)

·→ (conditional)

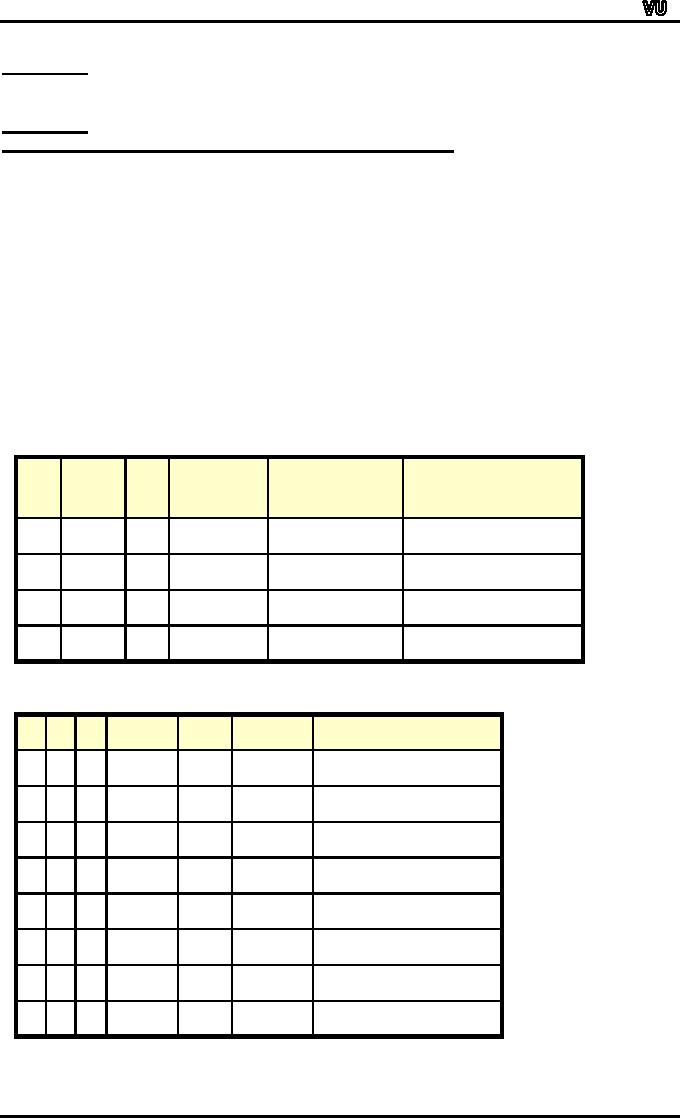
Construct a truth table for the statement form p ∨ ~ q → ~ p

p ∨ ~q

p∨~q→~p

Construct a truth table for the statement form (p →q)∧(~ p → r)

p→q

~p→r

(p→q)∧(~ p →r)

p q r

T T T

T T F

T F T

T F F

F T T

F T F

F F T

F F F

Page 11

MTH001 Elementary Mathematics

LOGICAL EQUIVALENCE INVOLVING IMPLICATION

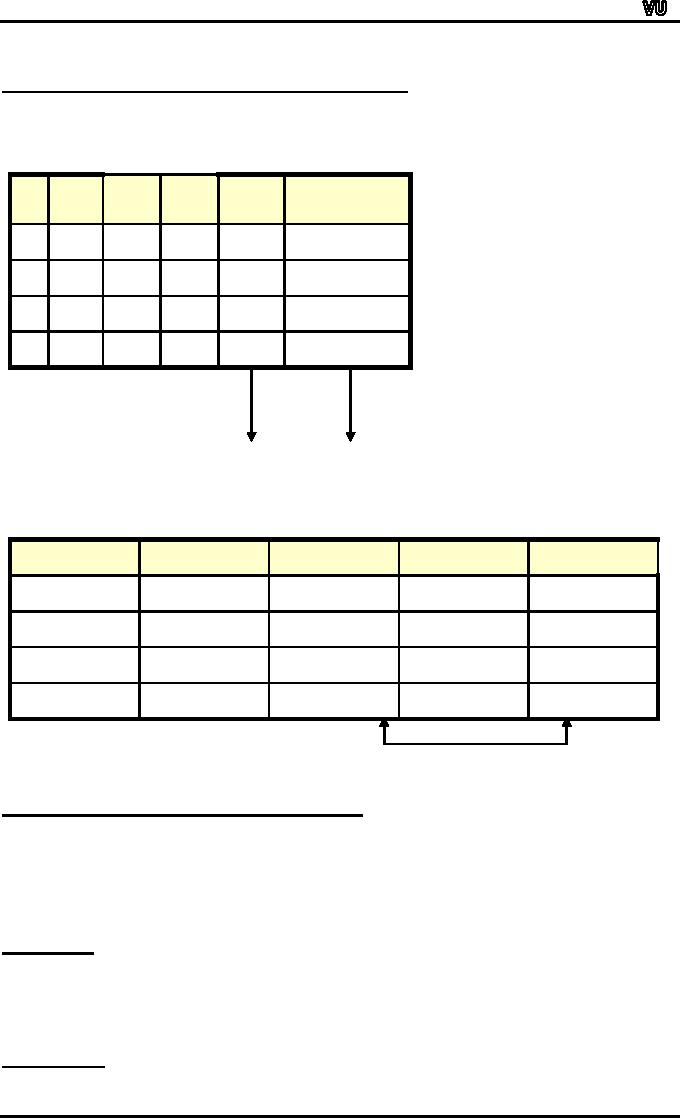
Use truth table to show p→q ≡ ~q → ~p

p→q

~q → ~p

same truth values

Hence the given two expressions are equivalent.

IMPLICATION LAW

p→q ≡ ~p∨q

p→q

~p∨q

same truth values

NEGATION OF A CONDITIONAL STATEMENT:

Since p→q ≡ ~p∨q therefore

~ (p → q) ≡ ~ (~ p ∨ q)

≡ ~ (~ p) ∧ (~ q) by De Morgan's law

≡ p ∧ ~ q by the Double Negative law

Thus the negation of "if p then q" is logically equivalent to "p and not q".

Accordingly, the negation of an if-then statement does not start with the word if.

EXAMPLES

Write negations of each of the following statements:

1.If Ali lives in Pakistan then he lives in Lahore.

2.If my car is in the repair shop, then I cannot get to class.

3.If x is prime then x is odd or x is 2.

4.If n is divisible by 6, then n is divisible by 2 and n is divisible by 3.

SOLUTIONS:

Page 12

MTH001 Elementary Mathematics

1. Ali lives in Pakistan and he does not live in Lahore.

2. My car is in the repair shop and I can get to class.

3.x is prime but x is not odd and x is not 2.

4.n is divisible by 6 but n is not divisible by 2 or by 3.

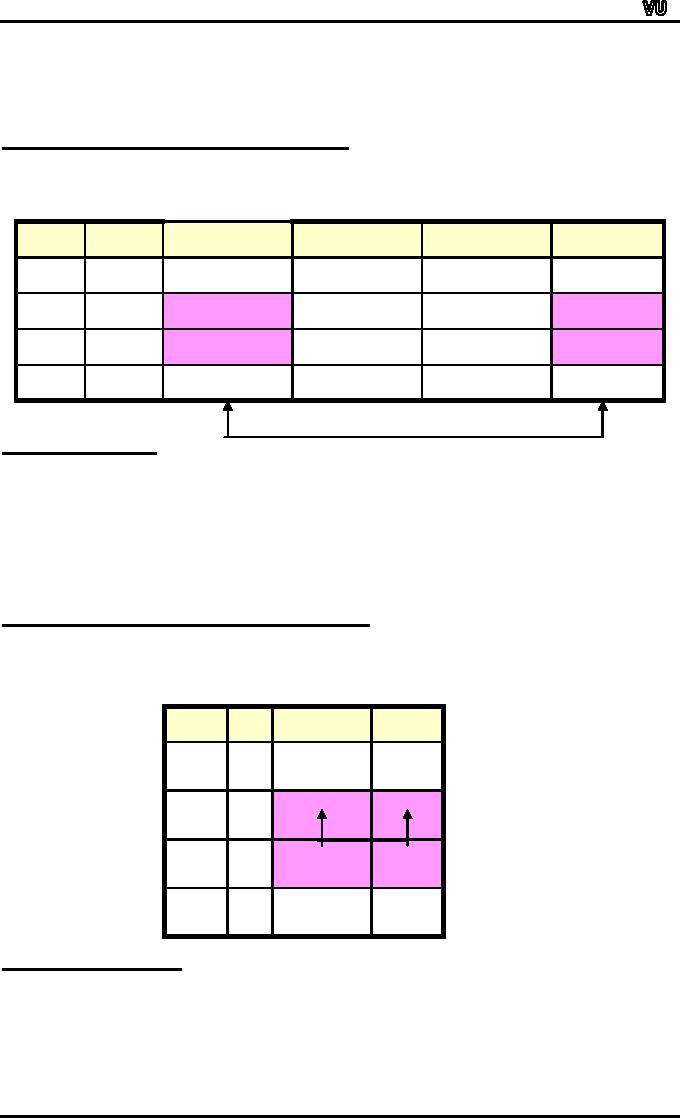
INVERSE OF A CONDITIONAL STATEMENT:

The inverse of the conditional statement p → q is ~p → ~q

A conditional and its inverse are not equivalent as could be seen from the truth table.

p→q

~p →~q

different truth values in rows 2 and 3

WRITING INVERSE:

1. If today is Friday, then 2 + 3 = 5.

If today is not Friday, then 2 + 3 ≠ 5.

2. If it snows today, I will ski tomorrow.

If it does not snow today I will not ski tomorrow.

3. If P is a square, then P is a rectangle.

If P is not a square then P is not a rectangle.

4. If my car is in the repair shop, then I cannot get to class.

If my car is not in the repair shop, then I shall get to the class.

CONVERSE OF A CONDITIONAL STATEMENT:

The converse of the conditional statement p → q is q →p

A conditional and its converse are not equivalent.

i.e., → is not a commutative operator.

p→q

q→p

not the same

WRITING CONVERSE:

1.If today is Friday, then 2 + 3 = 5.

If 2 + 3 = 5, then today is Friday.

2.If it snows today, I will ski tomorrow.

I will ski tomorrow only if it snows today.

3. If P is a square, then P is a rectangle.

Page 13

MTH001 Elementary Mathematics

If P is a rectangle then P is a square.

4. If my car is in the repair shop, then I cannot get to class.

If I cannot get to the class, then my car is in the repair shop.

CONTRAPOSITIVE OF A CONDITIONAL STATEMENT:

The contrapositive of the conditional statement p → q is~ q → ~ p

A conditional and its contrapositive are equivalent. Symbolically,p→q ≡ ~q → ~p

1.If today is Friday, then 2 + 3 = 5.

If 2 + 3 ≠ 5, then today is not Friday.

2.If it snows today, I will ski tomorrow.

I will not ski tomorrow only if it does not snow today.

3. If P is a square, then P is a rectangle.

If P is not a rectangle then P is not a square.

4. If my car is in the repair shop, then I cannot get to class.

If I get to the class, then my car is not in the repair shop.

Page 14

Table of Contents: