COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION

<< GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA

Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram >>

MTH001 Elementary Mathematics

LECTURE # 29

Permutations

Combinations

Random Experiment

Sample Space

Events

· Mutually Exclusive Events

· Exhaustive Events

· Equally Likely Events

COUNTING RULES:

As discussed in the last lecture, there are certain rules that facilitate the calculations

of probabilities in certain situations. They are known as counting rules and include concepts

of:

Multiple Choice

Permutations

Combinations

We have already discussed the rule of multiplication in the last lecture.

Let us now consider the rule of permutations.

RULE OF PERMUTATION:

A permutation is any ordered subset from a set of n distinct objects.

For example, if we have the set {a, b}, then one permutation is ab, and the other

permutation is ba.

The number of permutations of r objects, selected in a definite order from n distinct objects

is denoted by the symbol nPr, and is given by

nPr = n (n 1) (n 2) ...(n r + 1)

(n - r )!

FACTORIALS

7! = 7 × 6 × 5 × 4 × 3 × 2 × 1

6! = 6 × 5 × 4 × 3 × 2 × 1

1! = 1

Also, we define 0! = 1.

Example:

A club consists of four members. How many ways are there of selecting three officers:

president, secretary and treasurer?

It is evident that the order in which 3 officers are to be chosen, is of significance.

Thus there are 4 choices for the first office, 3 choices for the second office, and 2 choices

for the third office. Hence the total number of ways in which the three offices can be filled is

4 × 3 × 2 = 24.

The same result is obtained by applying the rule of permutations:

(4 - 3)!

= 4 × 3× 2

Page

204

= 24

MTH001 Elementary Mathematics

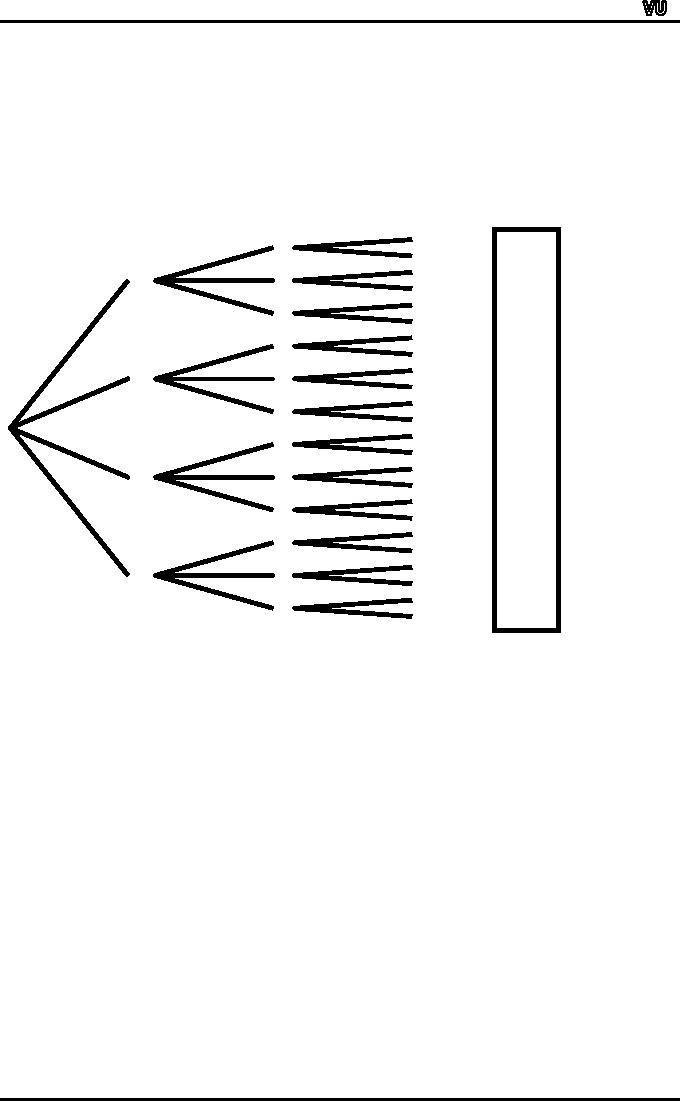
Let the four members be, A, B, C and D. Then a tree diagram which provides an organized

way of listing the possible arrangements, for this example, is given below:

President

Secretary

Treasurer

Sample Space

ABC

ABD

ACB

ACD

ADB

ADC

BAC

BAD

BCA

BCD

BDA

BDC

CAB

CAD

CBA

CBD

CDA

CDB

DAB

DAC

DBA

DBC

DCA

DCB

PERMUTATIONS:

In the formula of nPr, if we put r = n, we obtain:

nPn = n(n 1) (n 2) ... 3 × 2 × 1

= n!

I.e. the total number of permutations of n distinct objects, taking all n at a time, is equal to n!

EXAMPLE:

Suppose that there are three persons A, B & D, and that they wish to have a

photograph taken.

The total number of ways in which they can be seated on three chairs (placed side

by side) is

3P3 = 3! = 6

These are:

ABD,

ADB,

BAD,

BDA,

DAB,

DBA.

Page

205

MTH001 Elementary Mathematics

The above discussion pertained to the case when all the objects under consideration are

distinct objects. If some of the objects are not distinct, the formula of permutations modifies

as given below:

The number of permutations of n objects, selected all at a time, when n objects consist of n1

of one kind, n2 of a second kind, ..., nk of a kth kind,

is P =

n1 ! n 2 ! ..... n k !

(where ∑ n i = n )

EXAMPLE:

How many different (meaningless) words can be formed from the word `committee'?

In this example:

n = 9 (because the total number of letters in this word is 9)

n1 = 1 (because there is one c)

n2 = 1 (because there is one o)

n3 = 2 (because there are two m's)

n4 = 1 (because there is one i)

n5 = 2 (because there are two t's)

and

n6 = 2 (because there are two e's)

Hence, the total number of (meaningless) words

(permutations) is:

n1 ! n 2 ! ..... n k !

1! 1! 2! 1! 2! 2!

9 × 8 × 7 × 6 × 5 × 4 × 3× 2 ×1

1×1× 2 × 1×1× 2 × 1× 2 ×1

= 45360

Next, let us consider the rule of combinations.

RULE OF COMBINATION:

A combination is any subset of r objects, selected without regard to their order, from a set of

n distinct objects. The total number of such combinations is denoted by the symbol

⎛ n⎞

Cr or ⎜ ⎟,

⎜r ⎟

⎝ ⎠

and is given by

⎛n⎞

⎜ ⎟=

⎜ r ⎟ r!(n - r )!

⎝ ⎠

where r < n.

It should be noted that

Page

206

MTH001 Elementary Mathematics

⎛n⎞

Pr = r!⎜ ⎟

⎜r ⎟

⎝ ⎠

In other words, every combination of r objects (out of n objects) generates r! Permutations.

EXAMPLE:

Suppose we have a group of three persons, A, B, & C. If we wish to select a group of two

persons out of these three, the three possible groups are {A, B},

{A, C} and {B, C}.In other words, the total number of combinations of size two out of this set

of size three is 3.

Now, suppose that our interest lies in forming a committee of two persons, one of

whom is to be the president and the other the secretary of a club.

The six possible committees are:

(A, B) , (B, A),

(A, C) , (C, A),

(B, C) & (C, B).

In other words, the total number of permutations of two persons out of three is 6.

And the point to note is that each of three combinations mentioned earlier generates

2 = 2! permutations.

i.e. the combination {A, B} generates the permutations

(A, B) and (B, A);

the combination {A, C} generates the permutations

(A, C) and (C, A); and

the combination {B, C} generates the permutations

(B, C) and (C, B).

The quantity

⎛ n⎞

⎜ ⎟

⎜r ⎟

⎝ ⎠

or nCr is also called a binomial co-efficient because of its appearance in the binomial

expansion of

⎛ n ⎞ n-r r

(a + b)

=∑

⎜ ⎟a b .

⎜r ⎟

⎝ ⎠

r =0

The binomial co-efficient has two important properties.

⎛n⎞ ⎛ n ⎞

⎜ ⎟=⎜

⎜ r ⎟ ⎜ n - r ⎟, and

⎟

⎝ ⎠ ⎝

⎠

⎛ n ⎞ ⎛ n ⎞ ⎛ n + 1⎞

⎜n - r⎟ + ⎜r ⎟ = ⎜ r ⎟

⎜

ii)

⎟ ⎜ ⎟ ⎜

⎟

⎝

⎠ ⎝ ⎠ ⎝

⎠

Also, it should be noted that

⎛ n⎞

⎜ ⎟ =1= ⎜ ⎟

⎜ n⎟

⎜0⎟

⎝ ⎠

and

Virtual U⎛ n ⎞ rsity of⎛ akist⎞ n

nive

P n a

Page

⎜ ⎟=n=⎜

⎟

207

⎜ ⎟

⎜

⎟

⎝ n - 1⎠

⎝1 ⎠

MTH001 Elementary Mathematics

EXAMPLE:

A three-person committee is to be formed out of a group of ten persons. In how many ways

can this be done?

Since the order in which the three persons of the committee are chosen, is unimportant, it is

therefore an example of a problem involving combinations. Thus the desired number of

combinations is

⎛ n ⎞ ⎛10 ⎞

10!

⎜ ⎟=⎜ ⎟=

⎜ r ⎟ ⎜ 3 ⎟ 3! (10 - 3)! 3! 7!

⎝ ⎠ ⎝ ⎠

10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 ×1

3 × 2 ×1× 7 × 6 × 5 × 4 × 3 × 2 ×1

= 120

In other words, there are one hundred and twenty different ways of forming a three-person

committee out of a group of only ten persons!

EXAMPLE:

In how many ways can a person draw a hand of 5 cards from a well-shuffled ordinary deck

of 52 cards?

The total number of ways of doing so is given by

⎛ n ⎞ ⎛ 52 ⎞ 52 × 51× 50 × 49 × 48

⎜ ⎟=⎜ ⎟=

= 2,598,960

⎜ r ⎟ ⎜5 ⎟

5 × 4 × 3 × 2 ×1

⎝ ⎠ ⎝ ⎠

Having reviewed the counting rules that facilitate calculations of probabilities in a number of

problems, let us now begin the discussion of concepts that lead to the formal definitions of

probability.

The first concept in this regard is the concept of Random Experiment.

The term experiment means a planned activity or process whose results yield a set of data.

A single performance of an experiment is called a trial. The result obtained from an

experiment or a trial is called an outcome.

RANDOM EXPERIMENT:

An experiment which produces different results even though it is repeated a large

number of times under essentially similar conditions is called a Random Experiment.

The tossing of a fair coin, the throwing of a balanced die, drawing of a card from a well-

shuffled deck of 52 playing cards, selecting a sample, etc. are examples of random

experiments.

A random experiment has three properties:

i) The experiment can be repeated, practically or theoretically, any number of times.

ii )The experiment always has two or more possible outcomes. An experiment that has only

one possible outcome, is not a random experiment.

iii )The outcome of each repetition is unpredictable, i.e. it has some degree of uncertainty.

Page

208

MTH001 Elementary Mathematics

Considering a more realistic example, interviewing a person to find out whether or not he or

she is a smoker is an example of a random experiment. This is so because this example

fulfils all the three properties that have just been discussed:

1.This process of interviewing can be repeated a large number of times.

2.To each interview, there are at least two possible replies: `I am a smoker' and `I am not a

smoker'.

3.For any interview, the answer is not known in advance i.e. there is an element of

uncertainty regarding the person's reply.

A concept that is closely related with the concept of a random experiment is the concept of

the Sample Space.

SAMPLE SPACE:

A set consisting of all possible outcomes that can result from a random experiment

(real or conceptual), can be defined as the sample space for the experiment and is denoted

by the letter S.

Each possible outcome is a member of the sample space, and is called a sample point in

that space.

Let us consider a few examples:

EXAMPLE-1

The experiment of tossing a coin results in either of the two possible outcomes: a

head (H) or a tail (T).

(We assume that it is not possible for the coin to land on its edge or to roll away.)

The sample space for this experiment may be expressed in set notation as S = {H, T}.

`H' and `T' are the two sample points.

EXAMPLE-2

The sample space for tossing two coins once (or tossing a coin twice) will contain

four possible outcomes denoted by

S = {HH, HT, TH, TT}.

In this example, clearly, S is the Cartesian product A × A, where A = {H, T}.

EXAMPLE-3

The sample space S for the random experiment of throwing two six-sided dice can

be described by the Cartesian product A × A, where

A = {1, 2, 3, 4, 5,6}.

In other words,

S=A×A

= {(x, y) | x ∈ A and y ∈ A}

where x denotes the number of dots on the upper face of the first die, and y denotes the

number of dots on the upper face of the second die.

Hence, S contains 36 outcomes or sample points, as shown below:

S = { (1, 1), (1, 2), (1, 3), (1, 5), (1, 6),

(2, 1), (2, 2), (2, 3), (2, 5), (2, 6),

(3, 1), (3, 2), (3, 3), (3, 5), (3, 6),

(4, 1), (4, 2), (4, 3), (4, 5), (4, 6),

(5, 1), (5, 2), (5, 3), (5, 5), (5, 6),

(6, 1), (6, 2), (6, 3), (6, 5), (6, 6) }

The next concept is that of events:

EVENTS:

Any subset of a sample space S of a random experiment, is called an event.

In other words, an event is an individual outcome or any number of outcomes (sample

points) of a random experiment.

Page

209

MTH001 Elementary Mathematics

SIMPLE & COMPOUND EVENTS:

An event that contains exactly one sample point, is defined as a simple event. A

compound event contains more than one sample point, and is produced by the union of

simple events.

EXAMPLE

The occurrence of a 6 when a die is thrown, is a simple event, while the occurrence

of a sum of 10 with a pair of dice, is a compound event, as it can be decomposed into three

simple events (4, 6), (5, 5) and (6, 4).

OCCURRENCE OF AN EVENT:

An event A is said to occur if and only if the outcome of the experiment corresponds to some

element of A.

EXAMPLE:

Suppose we toss a die, and we are interested in the occurrence of an even number.

If ANY of the three numbers `2', `4' or `6' occurs, we say that the event of our interest has

occurred.

this

example,

the

event

represented

the

set

{2, 4, 6}, and if the outcome `2' occurs, then, since this outcome is corresponding to the first

element of the set A, therefore, we say that A has occurred.

COMPLEMENTARY EVENT:

The event "not-A" is denoted by ⎯A or Ac and called the negation (or complementary event)

of A.

EXAMPLE:

If we toss a coin once, then the complement of "heads" is "tails".

If we toss a coin four times, then the complement of "at least one head" is "no

heads".

A sample space consisting of n sample points can produce 2n different subsets (or simple

and compound events).

EXAMPLE:

Consider a sample space S containing 3 sample points, i.e. S = {a, b, c}.

Then the 23 = 8 possible subsets are

φ, {a}, {b}, {c}, {a, b},

{a, c}, {b, c}, {a, b, c}

Each of these subsets is an event.

The subset {a, b, c} is the sample space itself and is also an event. It always occurs and is

known as the certain or sure event.

The empty set φ is also an event, sometimes known as impossible event, because it can

never occur.

MUTUALLY EXCLUSIVE EVENTS:

Two events A and B of a single experiment are said to be mutually exclusive or disjoint if

and only if they cannot both occur at the same time i.e. they have no points in common.

EXAMPLE-1:

When we toss a coin, we get either a head or a tail, but not both at the same time.

The two events head and tail are therefore mutually exclusive.

EXAMPLE-2:

When a die is rolled, the events `even number' and `odd number' are mutually exclusive as

we can get either an even number or an odd number in one throw, not both at the same

time. Similarly, a student either qualifies or fails, a single birth must be either a boy or a girl,

it cannot be both, etc., etc. Three or more events originating from the same experiment are

mutually exclusive if pair wise they are mutually exclusive. If the two events can occur at the

same time, they are not mutually exclusive, e.g., if we draw a card from an ordinary deck of

52 playing cars, it can be both a king and a diamond.

Therefore, kings and diamonds are not mutually exclusive.

Similarly, inflation and recession are not mutually exclusive events.

Page

210

MTH001 Elementary Mathematics

Speaking of playing cards, it is to be remembered that an ordinary deck of playing cards

contains 52 cards arranged in 4 suits of 13 each. The four suits are called diamonds, hearts,

clubs and spades; the first two are red and the last two are black.

The face values called denominations, of the 13 cards in each suit are ace, 2, 3, ..., 10,

jack, queen and king.

The face cards are king, queen and jack.

These cards are used for various games such as whist, bridge, poker, etc.

We have discussed the concepts of mutually exclusive events.

Another important concept is that of exhaustive events.

EXHAUSTIVE EVENTS:

Events are said to be collectively exhaustive, when the union of mutually exclusive events is

equal to the entire sample space S.

EXAMPLES:

1. In the coin-tossing experiment, `head' and `tail' are collectively exhaustive events.

2. In the die-tossing experiment, `even number' and `odd number' are collectively exhaustive

events.

In conformity with what was discussed in the last lecture:

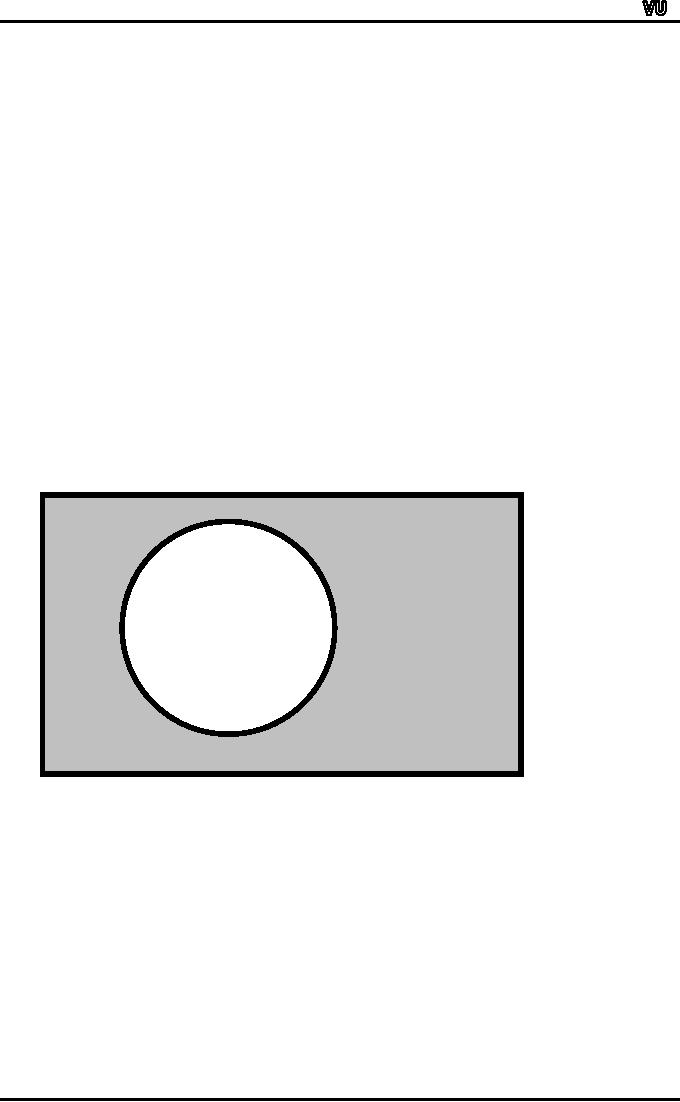
PARTITION OF THE SAMPLE SPACE:

A group of mutually exclusive and exhaustive events belonging to a sample space is

called a partition of the sample space. With reference to any sample space S, events A and

⎯A form a partition as they are mutually exclusive and their union is the entire sample space.

The Venn Diagram below clearly indicates this point.

⎯A is shaded

Next, we consider the concept of equally likely events:

EQUALLY LIKELY EVENTS:

Two events A and B are said to be equally likely, when one event is as likely to occur as the

other.

In other words, each event should occur in equal number in repeated trials.

EXAMPLE:

When a fair coin is tossed, the head is as likely to appear as the tail, and the

proportion of times each side is expected to appear is 1/2.

EXAMPLE:

If a card is drawn out of a deck of well-shuffled cards, each card is equally likely to

be drawn, and the probability that any card will be drawn is 1/52.

Page

211

Table of Contents: