 |
GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION: |
| << GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE |
| GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA >> |
MTH001
Elementary Mathematics
LECTURE #
27:
�
Concept of
dispersion
�
Absolute
and relative measures of
dispersion
�
Range
�
Coefficient
of dispersion
�
Quartile
deviation
�
Coefficient
of quartile deviation
Let
us begin the concept of
DISPERSION.
Just
as variable series differ
with respect to their
location on the horizontal
axis (having
different
`average' values); similarly,
they differ in terms of the
amount of variability
which
they
exhibit.
Let
us understand this point
with the help of an
example:
EXAMPLE:
In
a technical college, it may
well be the case that
the ages of a group of
first-year students
are
quite consistent, e.g. 17,
18, 18, 19, 18,
19, 19, 18, 17, 18
and 18 years.
A
class of evening students
undertaking a course of study in
their spare time may
show just
the
opposite situation, e.g. 35,
23, 19, 48, 32,
24, 29, 37, 58,
18, 21 and 30.
It
is very clear from this
example that the variation
that exists between the
various values of
a
data-set is of substantial importance. We
obviously need to be aware of
the amount of
variability
present in a data-set if we are to
come to useful conclusions
about the situation
under
review. This is perhaps best
seen from studying the
two frequency distributions
given
below:
EXAMPLE:
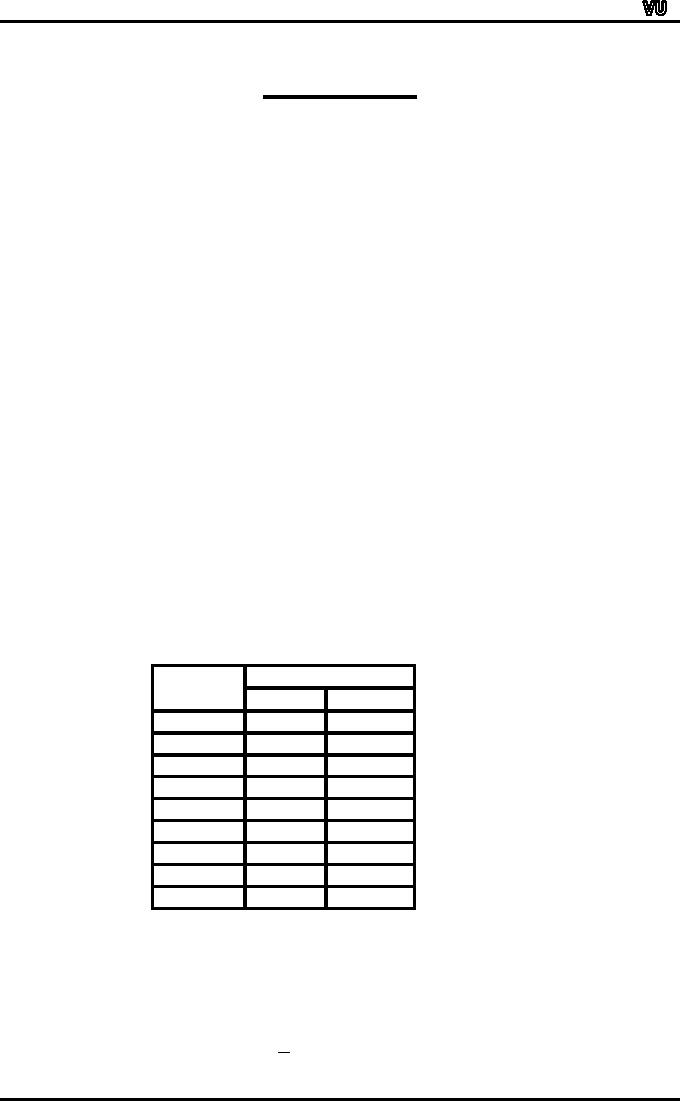
The
sizes of the classes in two
comprehensive schools in different
areas are as
follows:
Number
Number
of Classes
of
Pupils
Area
A
Area
B
10
14
0
5
15
19
3
8
20
24
13
10
25
29
24
12
30
34
17
14
35
39
3
5
40
44
0
3
45
- 49
0
3
60
60
If
the arithmetic mean size of
class is calculated, we discover
that the answer is
identical:
27.33
pupils in both areas.
Average
class-size of each
school
X
=
27.33
Page
188
MTH001
Elementary Mathematics
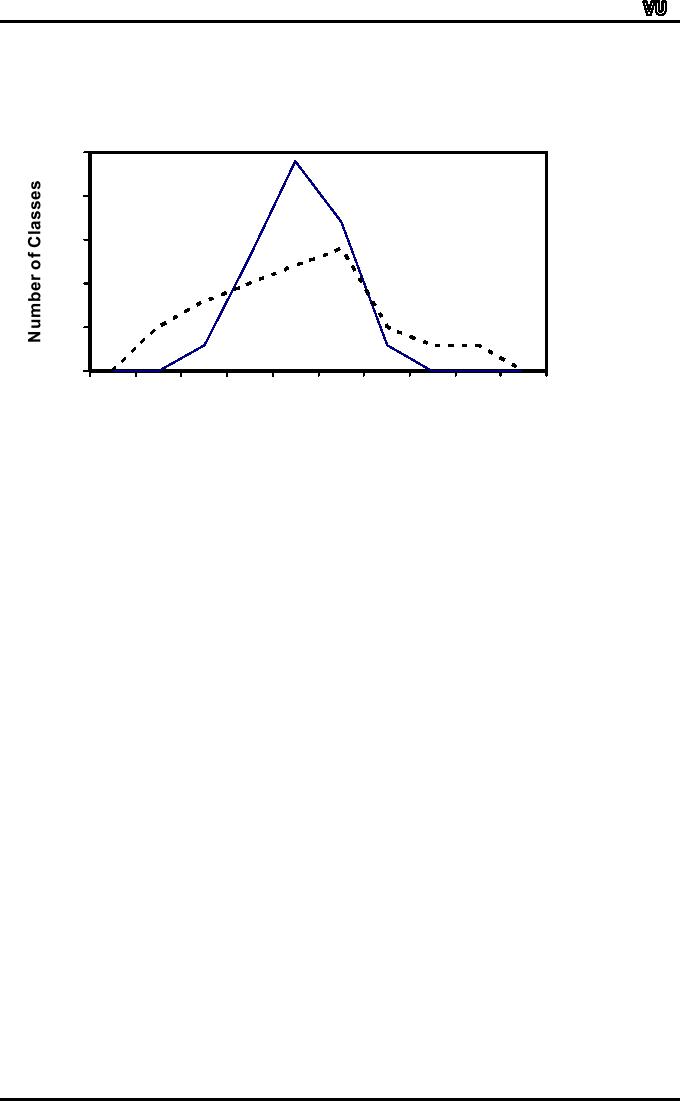
Even
though these two
distributions share a common
average, it can readily be
seen that
they
are entirely
DIFFERENT.
And
the graphs of the two
distributions (given below)
clearly indicate this
fact.
25
Area
20
A
15
10
Area
5
B
0
9
4
4
9
4
9
4
9
4
9
1
0 2 5 2 0 3 5 3 0 4 4 -4 0
5
1
4
0
15
4
5
4
3
3
2
2
1
Number
of Pupils
The
question which must be posed
and answered is `In what
way can these two
situations
be
distinguished?'
We
need a measure of variability or
DISPERSION to accompany the
relevant
measure
of position or `average'
used.
The
word `relevant' is important
here for we shall find
one measure of
dispersion
which
expresses the scatter of
values round the arithmetic
mean, another the scatter
of
values
round the median, and so
forth. Each measure of
dispersion is associated with
a
particular
`average'.
Absolute
versus Relative Measures of
Dispersion:
There
are two types of
measurements of dispersion: absolute
and relative.
An
absolute
measure of
dispersion is one that
measures the dispersion in
terms of
the
same units or in the square
of units, as the units of
the data.
For
example, if the units of the
data are rupees, meters,
kilograms, etc., the units
of
the
measures of dispersion will
also be rupees, meters,
kilograms, etc.
On
the other hand,
relative
measure of
dispersion is one that is
expressed in the
form
of a ratio, co-efficient of percentage
and is independent of the
units of measurement.
A
relative
measure of
dispersion is useful for
comparison of data of different
nature.
A
measure of central tendency
together with a measure of
dispersion gives an
adequate
description
of data. We will be discussing
FOUR measures of dispersion
i.e. the range,
the
quartile
deviation, the mean
deviation, and the standard
deviation.
RANGE:
The
range is defined as the
difference between the two
extreme values of a
data-set,
i.e.
R = Xm X0 where Xm represents the
highest value and X0 the
lowest.
Evidently,
the calculation of the range
is a simple question of MENTAL
arithmetic.
The
simplicity of the concept
does not necessarily
invalidate it, but in
general it gives no
idea
of
the DISTRIBUTION of the
observations between the two
ends of the series. For
this
reason
it is used principally as a supplementary
aid in the description of
variable data, in
conjunction
with other measures of
dispersion. When the data
are grouped into a
frequency
distribution,
the range is estimated by
finding the difference
between the upper boundary
of
the
highest class and the
lower boundary of the lowest
class.
Page
189
MTH001
Elementary Mathematics
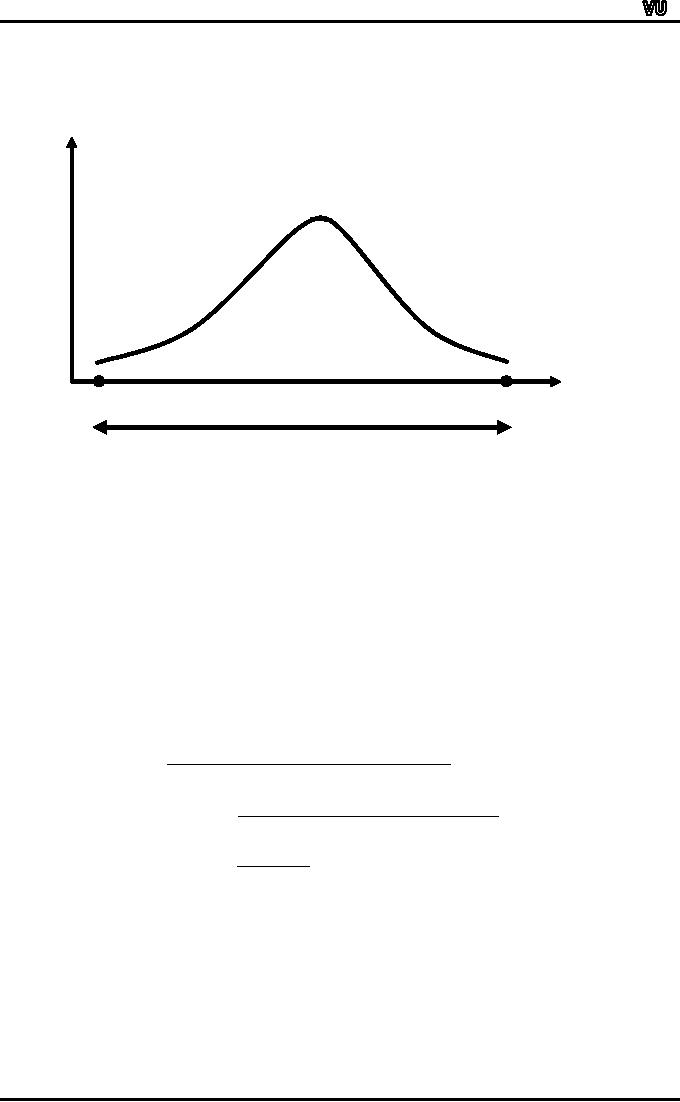
We
now consider the graphical
representation of the
range:
f
X
X0
Xm
Rang
Obviously,
the greater the difference
between the largest and
the smallest values,
the
greater
will be the range. As stated
earlier, the range is a
simple concept and is easy
to
compute.
However, because of the fact
that it is computed from
only the two extreme
values
in
a data-set,
it has
two serious
disadvantages.
1.
It ignores
all
the INFORMATION available
from the intermediate
observations.
2.
It might give a MISLEADING
picture of the spread in the
data.
From
THIS point of view, it is an
unsatisfactory measure of dispersion.
However, it is
APPROPRIATELY
used in statistical quality
control charts of manufactured
products, daily
temperatures,
stock prices, etc.
It
is interesting to note that
the range can also be
viewed in the following
way:
It
is twice of the arithmetic
mean of the deviations of
the smallest and largest
values round
the
mid-range i.e.
(Midrange
-
X0 )
+ (X
m -
Midrange
)
2
Midrange
-
X0 +
X m -
Midrange
=
2
X
-
X0
= m
2
Because
of what has been just
explained, the range can be
regarded as that measure
of
dispersion
which is associated with the
mid-range. As such, the
range may be employed
to
indicate
dispersion when the
mid-range has been adopted
as the most appropriate
average.
The
range is an absolute
measure of
dispersion. Its relative
measure is
known as the CO-
EFFICIENT
OF DISPERSION, and is defined by
the relation given
below:
Coefficient
of Dispersion:
Page
190
MTH001
Elementary Mathematics
(Range)
1
2
=
Mid
-
Range
Xm -
X0
X
-
X0
2
= m
=
Xm +
X0
Xm +
X0
2
This
is a pure
(i.e.
dimensionless)
number and is
used for the purposes of
COMPARISON.
(This
is so because a pure number
can
be compared
with another pure
number.)
For
example, if the coefficient of
dispersion for one data-set
comes out to be 0.6
whereas
the coefficient of dispersion
for another data-set comes
out to be 0.4, then it
is
obvious
that there is greater amount
of dispersion in the first
data-set as compared with
the
second.
QUARTILE
DEVIATION:
The
quartile deviation is defined as
half of the difference
between the third and
first
quartiles
i.e.
Q3 -
Q1
Q.D.
=
2
It
is also known as semi-interquartile
range.
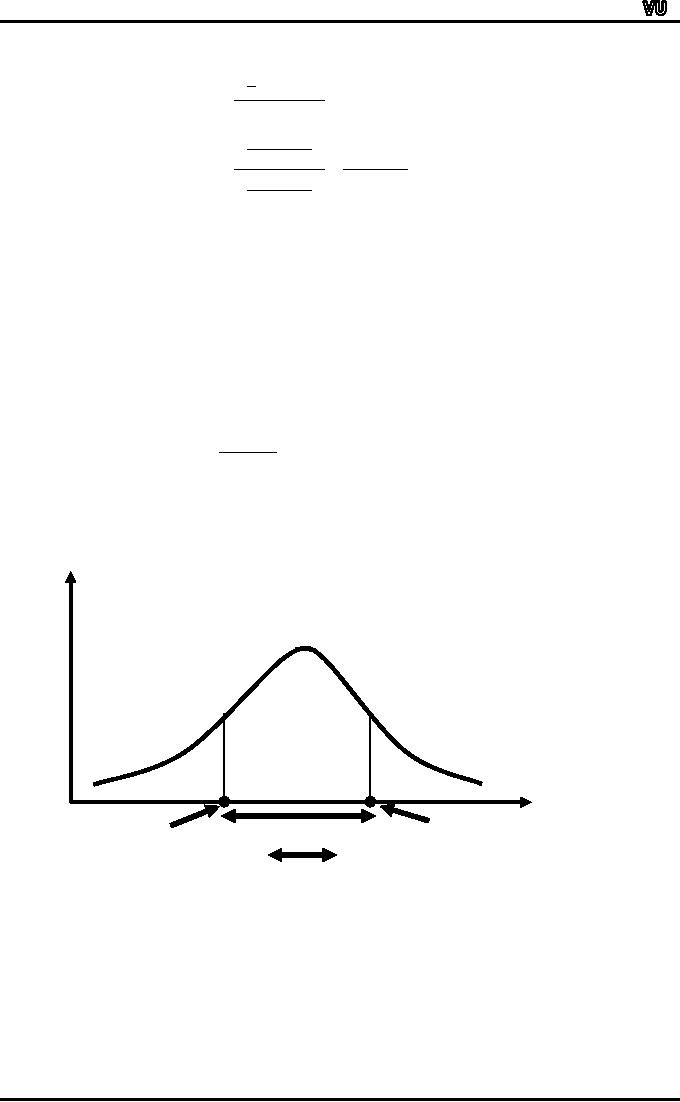
Let
us now consider the
graphical representation of the
quartile deviation:
f
X
Inter-quartile
Q1
Q3
Quartile
Deviation
(Semi
Inter-quartile Range)
Although
simple to compute, it is NOT an
extremely satisfactory measure of
dispersion
because
it takes into account the
spread of only two values of
the variable round
the
median,
and this gives no idea of
the rest of the dispersion
within the
distribution.
The
quartile deviation has an
attractive feature that the
range "Median + Q.D."
contains
approximately 50% of the
data.
This
is illustrated in the figure
given below:
Page
191
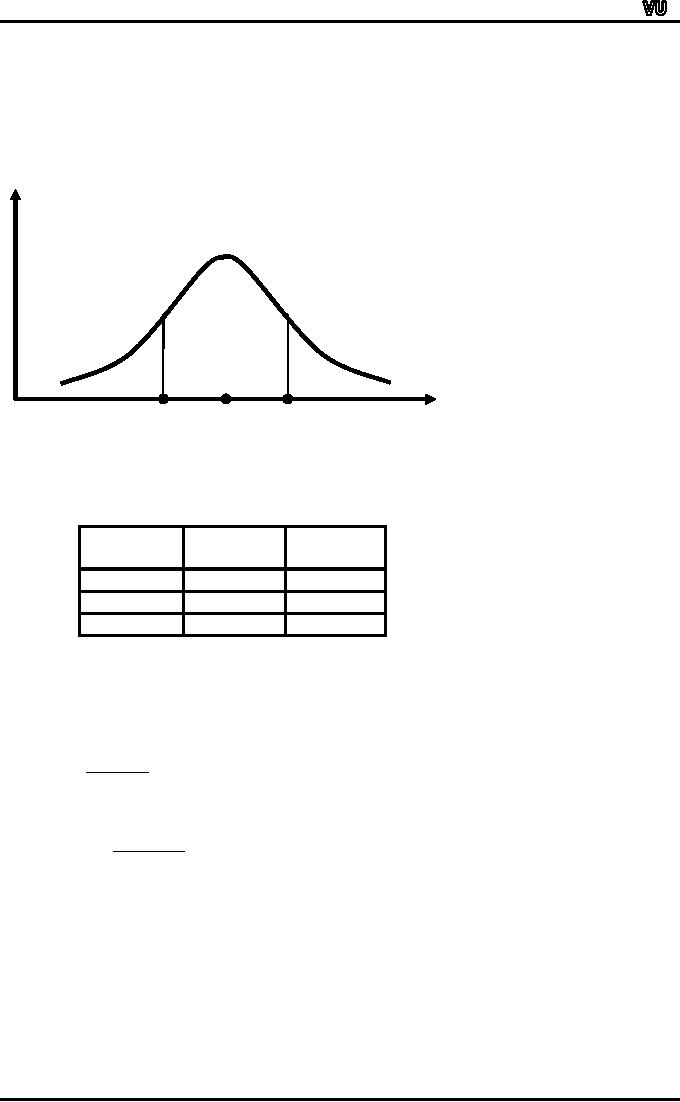
MTH001
Elementary Mathematics
f
50%
X
Median-Q.D.
Median
Median+Q.D.
Let
us now apply the concept of
quartile deviation to the
following example:
EXAMPLE:
The
shareholding structure of two
companies is given
below:
Company
Company
X
Y
1st quartile
60
shares
165
shares
Median
185
shares
185
shares
3rd quartile
270
shares
210
shares
The
quartile deviation for
company X is
270
-
60
=
105
Shares
2
For
company Y, it is
210
-
165
=
22
Shares
2
A
comparison of the above two
results indicate that there
is a considerable concentration of
shareholders
about the MEDIAN number of
shares in company Y, whereas in
company X,
there
does not exist this
kind of a concentration around
the median. (In company X,
there is
approximately
the SAME numbers of small,
medium and large
shareholders.)
From
the above example, it is
obvious that the larger
the quartile deviation,
the
greater
is the scatter of values
within the series. The
quartile deviation is superior to
range
as
it is not affected by extremely
large or small observations. It is
simple to understand
and
easy
to calculate.
The
mean deviation can also be
viewed in another
way:
Page
192

MTH001
Elementary Mathematics
It
is the arithmetic mean of
the deviations of the first
and third quartiles round
the median i.e.
(M
-
Q1 )
+ (Q3 -
M )
2
M
-
Q1 +
Q3 -
M
=
2
Q
-
Q1
= 3
2
Because
of what has been just
explained, the quartile
deviation is regarded as that
measure
of
dispersion which is associated
with the median. As such,
the quartile deviation
should
always
be employed to indicate dispersion
when the median has
been adopted as the
most
appropriate
average.
The
quartile deviation is also an
absolute
measure of
dispersion. Its relative
measure
called
the
CO-EFFICIENT OF QUARTILE DEVIATION or of
Semi-Inter-quartile Range, is
defined
by
the relation:
Coefficient
of Quartile Deviation:
Quartile
Deviation
=
Mid
-
Quartile
Range
Q3 -
Q1
Q
-
Q1
2
= 3
=
,
Q3 +
Q1
Q3 +
Q1
2
The
Coefficient of Quartile Deviation is a
pure number and is used
for COMPARING
the
variation
in two or more sets of
data.
The
next two measures of
dispersion to be discussed are
the Mean Deviation and
the
Standard
Deviation. In this regard,
the first thing to note is
that, whereas the range as
well
as
the quartile deviation are
two such measures of
dispersion which are NOT
based on all
the
values, the mean deviation
and the standard deviation
are two such measures
of
dispersion
that involve each and
every data-value in their
computation.
The
range measures the
dispersion of the data-set
around the mid-range,
whereas
the
quartile deviation measures
the dispersion of the
data-set around the
median.
How
are we to decide upon the
amount of dispersion round
the arithmetic
mean?
It
would seem reasonable to
compute the DISTANCE
of each
observed value in the
series
from
the arithmetic mean of the
series.
But
the problem is that the
sum of the deviations of the
values from the mean
is
ZERO!
(No matter what the
amount of dispersion in a data-set
is, this quantity will
always
be
zero,
and hence it cannot be used
to measure the dispersion in
the data-set.)
Then,
the question arises, `HOW
will we be able to measure
the dispersion present in
our
data-set?'
In
an attempt to answer this
question, we might look at
the numerical
differences
between
the mean and the
data values WITHOUT
considering whether these
are positive or
negative.
By ignoring the sign of the
deviations we will achieve a
NON-ZERO sum, and
Page
193

MTH001
Elementary Mathematics
averaging
these absolute differences,
again, we obtain a non-zero
quantity which can be
used
as a measure of dispersion. (The
larger this quantity, the
greater is the dispersion
in
the
data-set).
This
quantity is known as the
MEAN
DEVIATION.
Let
us denote these absolute
differences
by
`modulus of d'
or
`mod d'. Then, the
mean deviation is given
by
MEAN
DEVIATION:
∑|
d |
M.D.
=
n
As
the absolute deviations of
the observations from their
mean are being
averaged,
therefore
the complete name of this
measure is Mean Absolute
Deviation --- but generally,
it
is
simply called "Mean
Deviation". In the next
lecture, this concept will
be discussed in detail.
(The
case of raw data as well as
the case of grouped data
will be considered.)Next, we
will
discuss
the most important and
the most widely used
measure of dispersion i.e.
the
Standard
Deviation.
Page
194
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS