MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES

<< Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS

RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION >>

MTH001 Elementary Mathematics

LECTURE # 20

MATRICES

OBJECTIVES

The objectives of the lecture are to learn about:

Matrices

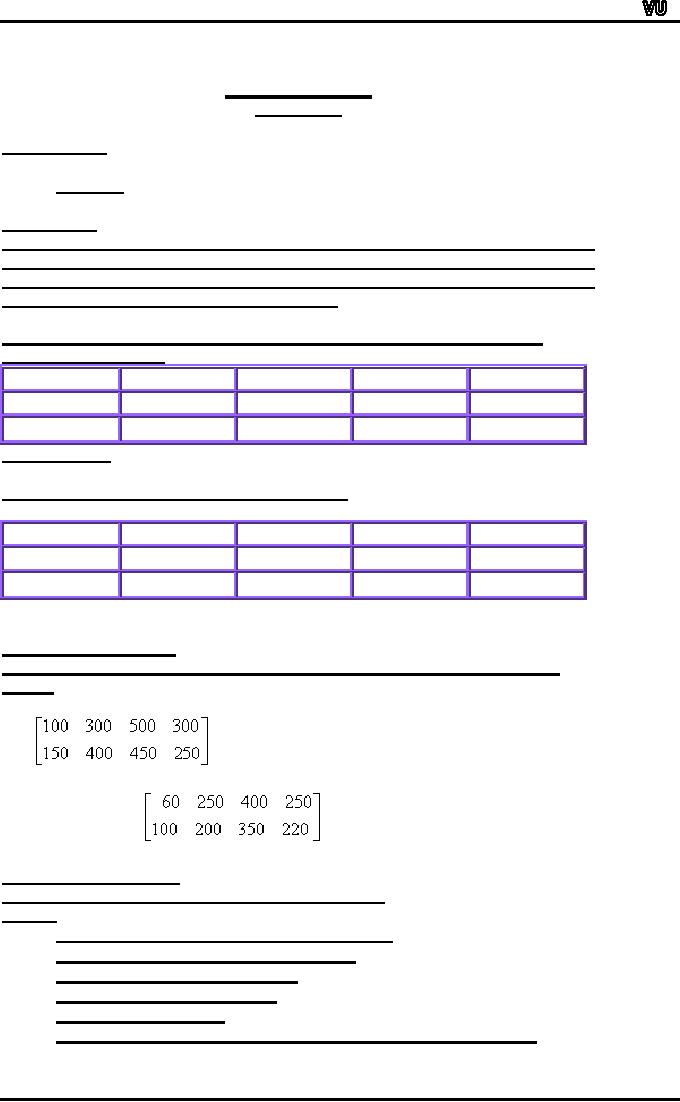
EXAMPLE 1

An athletic clothing company manufactures T-shirts and sweat shirts in four

differents sizes, small, medium, large, and x-large. The company supplies two

major universities, the U of R and the U of S. The tables below show

September's clothing order for each university

University of S's September Clothing Order

T-shirts

100

300

500

300

sweat shirts

150

400

450

250

University of R's September Clothing Order.

T-shirts

250

400

250

sweat shirts

100

200

350

200

Matrix Representation

The above information can be given by two matrices S and R as shown

below.

MATRIX OPERATIONS

The matrix operations can be summarized as under:

Organize and interpret data using matrices

Use matrices in business applications

Add and subtract two matrices

Multiply a matrix by a scalar

Multiply two matrices

Interpret the meaning of the elements within a product matrix

Page

132

MTH001 Elementary Mathematics

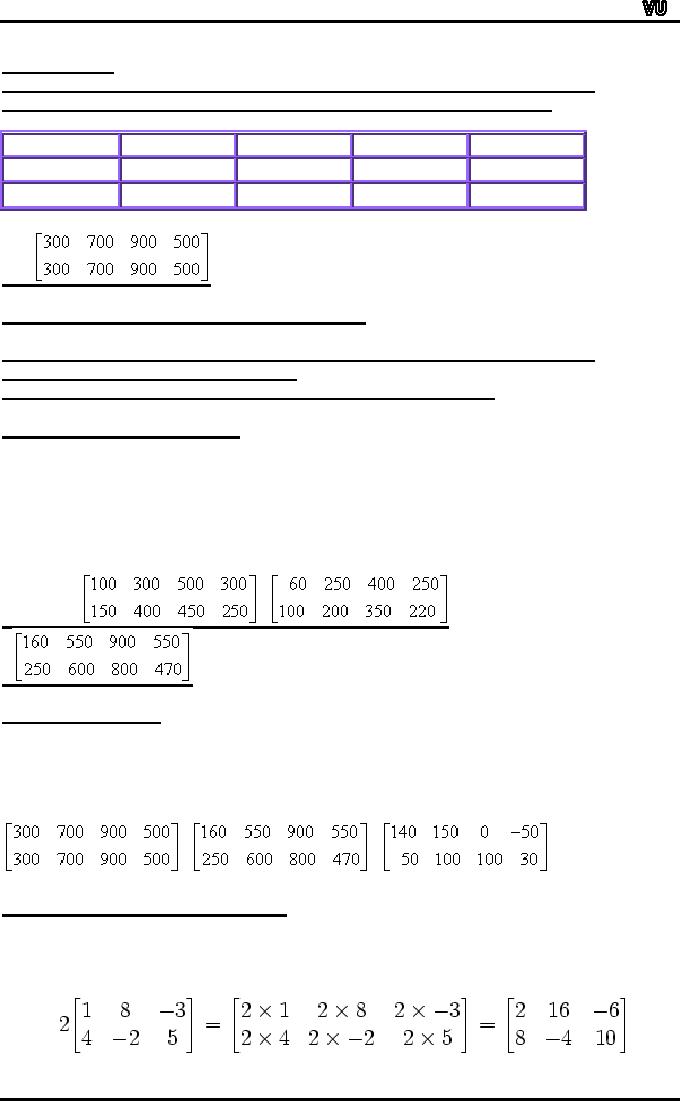
PRODUCTION

The clothing company production in preparation for the universities'

September orders is shown by the table and corresponding matrix P below.

T-shirts

300

700

900

500

sweat shirts

300

700

900

500

ADDITION AND SUBTRACTION OF MATRICES

The sum or difference of two matrices is calculated by adding or subtracting the

corresponding elements of the matrices.

To add or subtract matrices, they must have the same dimensions.

PRODUCTION REQUIREMENT

Since the U of S ordered 100 small T-shirts and the U of R ordered 60, then

althogether 160 small T-shirts are required to supply both universities. Thus, to

calculate the total number of T-shirts and sweat shirts required to supply both

universities, add the corresponding elements of the two order matrices as shown

below.

OVERPRODUCTION

Since the company produced 300 small T-shirts and the received orders for only

160 small T-shirts, then the company produced 140 small T-shirts too many.

Thus, to determine the company's over-production, subtract the corresponding

elements of the total order matrix from the production matrix as shown below.

MULTIPLY A MATRIX BY A SCALAR

Given a matrix A and a number c, the scalar multiplication cA is computed by multiplying the scalar

c by every element of A .For example:

Page

133

MTH001 Elementary Mathematics

MULTIPLICATION OF MATRICES

To understand the reasoning behind the definition of matrix multiplication,

let us consider the following example.

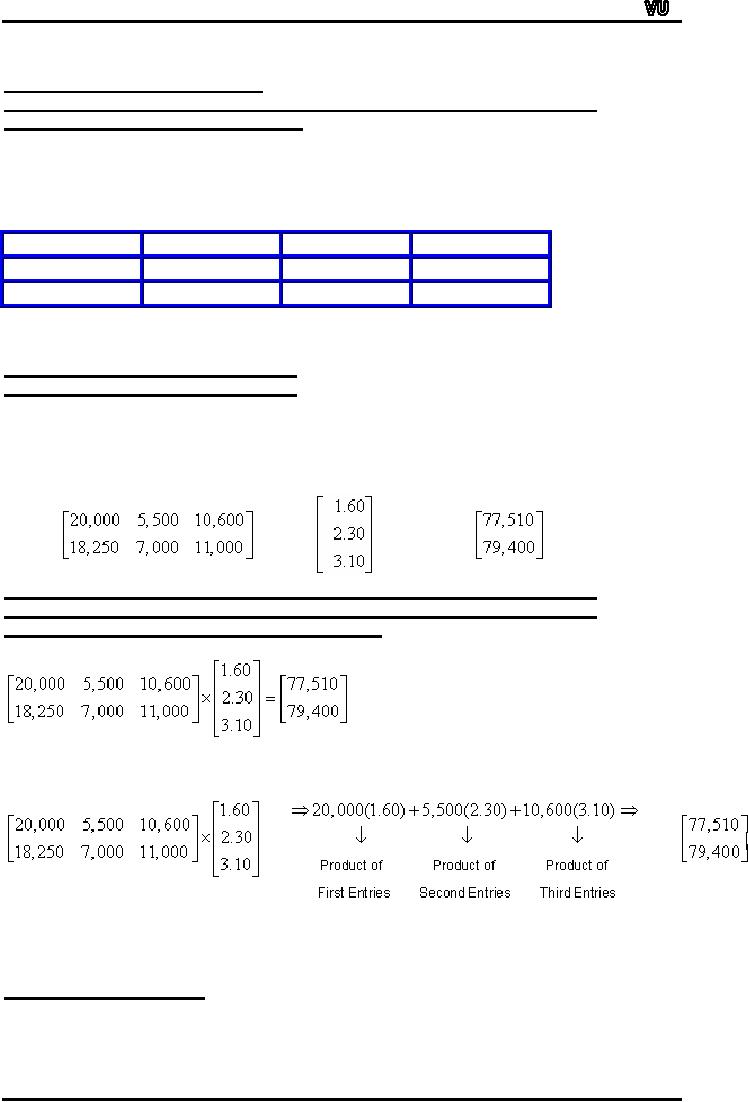
Competing Companies, A and B, sell juice in 591 mL, 1 L and 2 L plastic bottles

at prices of Rs.1.60, Rs.2.30 and Rs.3.10, respectively. The table below

summarises the sales for the two companies during the month of July.

591mL

Company A

20,000

5,500

10,600

Company B

18,250

7,000

11,000

What is total revenue of Company A?

What is total revenue of Company B?

Matrices may be used to illustrate the above information.

As shown at the right, the sales can be written as

a 2X3 matrix, S, the selling prices can be written as a column matrix, P, and the

total revenue for each company can be expressed as a column matrix, R.

Since revenue is calculated by multiplying the number of sales by the

selling price, the total revenue for each company is found by taking the

product of the sales matrix and the price matrix.

Consider how the first row of matrix S and the single column P lead to the

first entry of R.

With the above in mind, we define the product of a row and a column to be the

number obtained by multiplying corresponding entries (first by first, second by

second, and so on) and adding the results.

MULTIPLICATION RULES

Page

134

MTH001 Elementary Mathematics

If matrix A is a m n matrix and matrix B is a n p matrix, then the product AB is

the m p matrix whose entry in the i-th row and the j-th column is the product of

the i-th row of matrix A and the j-th row of matrix B.

The product of a row and a column is the number obtained by multiplying

corresponding elements (first by first, second by second, and so on).

To multiply matrices, the number of columns of A must equal the number of rows

of B.

MULTIPLICATION RULES For example

Given the matrices below, decide if the indicated product exists. And, if the

product exists, determine the dimensions of the product matrix.

MULTIPLICATION CHECKS

The table below gives a summary whether it is possible to multiply two matrices.

It may be noticed that the product of matrix A and matrix B is possible as the

number of columns of A are equal to the number of rows of B. The product BA is

not possible as the number of columns of b are not equal to rows of A.

Page

135

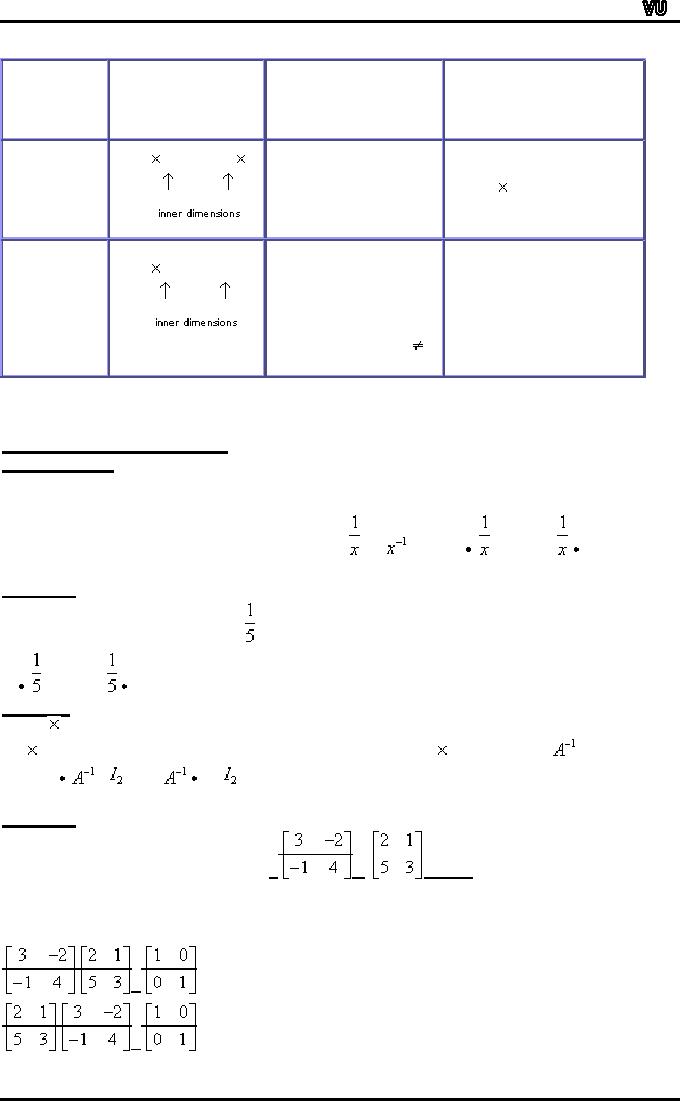
MTH001 Elementary Mathematics

Does a product exist?

Dimensions of (Is it possible to multiply Dimensions of

Product

the Matrices

the given

Product Matrix

matrices in this order?)

Yes, the product exists

A=3 3 B=3 2

since the

inner dimensions match

(# of columns of A = #

of rows of B).

No, the product does

B=3 2

A = 3×3

not exist

since the inner

dimensions do

n/a

not match

(# of columns of B #

of rows of A).

MULTIPLICATIVE INVERSES

Real Numbers

Two non-zero real numbers are multiplicative inverses of each other if their

products, in both orders, is 1. Thus,

the multiplicative inverse of a real number, x is

since x

= 1 and

= 1.

Example:

The multiplicative inverse of 5 is

since

= 1 and

5=1

Matrices

Two 2 2 matrices are inverses of each other if their products, in both orders, is

a 2 2 identity matrix. Thus, the multiplicative inverse of a 2 2 matrix, A is

since A

and

Example:

⎡ 3 -1⎤

The multiplicative inverse of a matrix,

since is ⎢

-5 2 ⎥

⎣

⎦

Page

136

MTH001 Elementary Mathematics

-1⎤ ⎡ 1 0⎤

⎡2

1⎤ ⎡ 3

⎥ = ⎢ 0 1⎥

⎢5

3⎥ ⎢-5

2⎦ ⎣

⎣

⎦⎣

⎦

-1⎤ ⎡2

⎡3

1⎤ ⎡ 1 0⎤

⎢-5

2 ⎥ ⎢5

3⎥ ⎢ 0 1⎥

⎣

⎦⎣

⎦

Page

137

Table of Contents: