ZeePedia

Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY

<< Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS >>
img
MTH001 ­ Elementary Mathematics
LECTURE #2
Truth Tables for:
~p∧q
1.
~ p ∧ (q ∨ ~ r)
2.
(p∨q) ∧ ~ (p∧q)
3.
Truth table for the statement form ~ p ∧ q
~p∧q
p
q
~p
T
T
F
F
T
F
F
F
F
T
T
T
F
F
T
F
Truth table for ~ p ∧ (q ∨ ~ r)
q∨~r
~ p ∧ (q ∨ ~ r)
~
p
q
r
~p
r
T
T
T
F
T
F
F
T
T
F
T
T
F
F
T
F
T
F
F
F
F
T
F
F
T
T
F
F
F
T
T
F
T
T
T
F
T
F
T
T
T
T
F
F
T
F
F
T
F
F
F
F
T
T
T
T
Truth table for (p∨q) ∧ ~ (p∧q)
p∨q
p∧q
~ (p∧q)
(p∨q) ∧ ~ (p∧q)
p
q
T
T
T
T
F
F
T
F
T
F
T
T
F
T
T
F
T
T
F
F
F
F
T
F
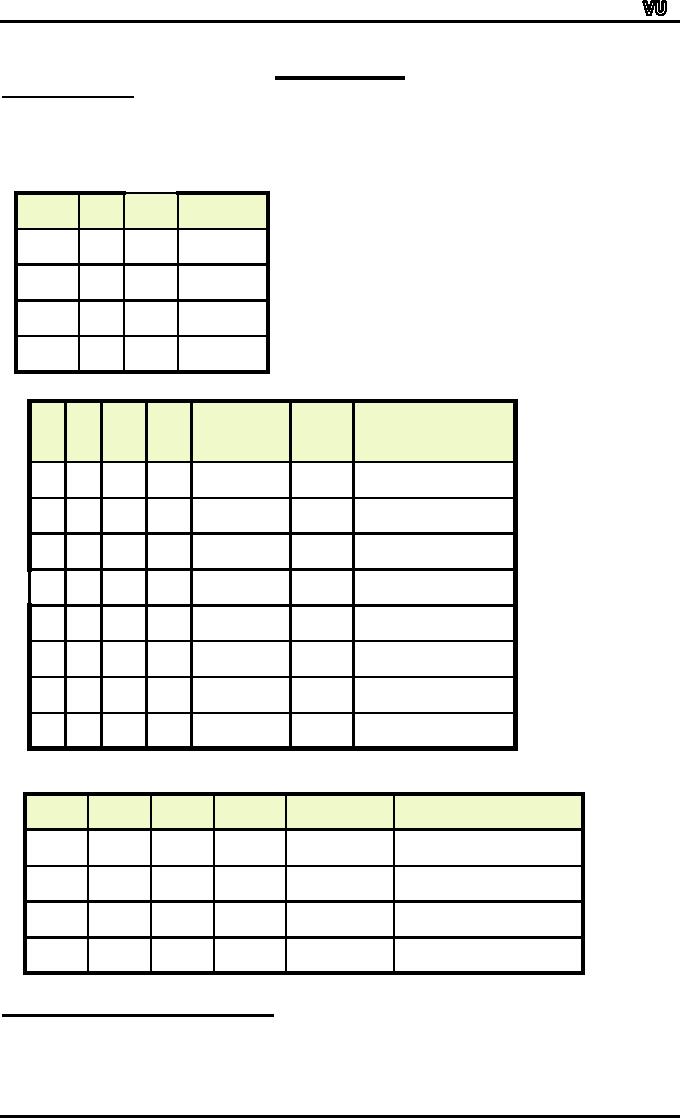
Double Negative Property ~(~p) º p
Page 6
img
MTH001 ­ Elementary Mathematics
p
~p
~(~p)
T
F
T
F
T
F
Example
"It is not true that I am not happy"
Solution:
Let p = "I am happy"
then ~ p = "I am not happy"
and ~(~ p) = "It is not true that I am not happy"
Since ~(~p) ≡ p
Hence the given statement is equivalent to:
"I am happy"
~(p∧q) and ~p ∧ ~q are not logically equivalent
p∧q
~(p∧q)
~p ∧ ~q
p
q
~p
~q
T
T
F
F
T
F
F
T
F
F
T
F
T
F
F
T
T
F
F
T
F
Different Futh values inTow 2 and row 3  T
F   tr
T
F
T
r
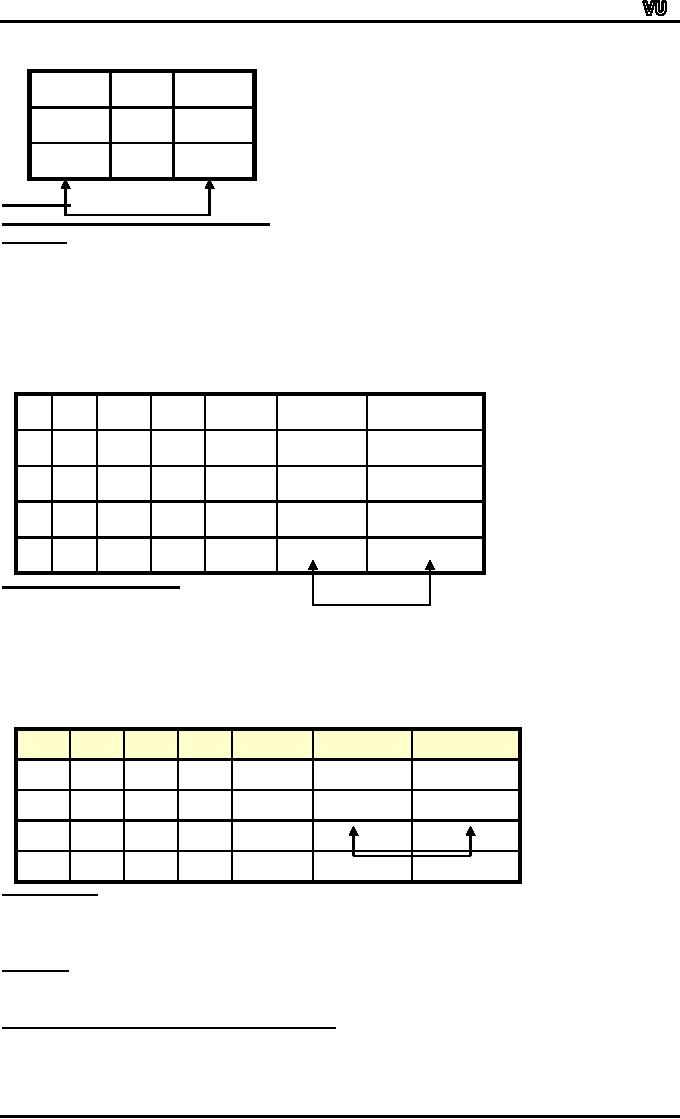
DE MORGAN'S LAWS:
1)The negation of an and statement is logically equivalent to the or
statement in which each component is negated.
Symbolically ~(p ∧ q) ≡ ~p ∨ ~q.
2)The negation of an or statement is logically equivalent to the and
statement in which each component is negated.
Symbolically: ~(p ∨ q) ≡ ~p ∧ ~q.
~(p ∨ q) ≡ ~p ∧ ~q
p∨q
~(p ∨ q)
~p ∧ ~q
p
q
~p
~q
T
T
F
F
T
F
F
T
F
F
T
T
F
F
F
T
T
F
T
F
F
F
F
T
T
F
Same truth valuTs
T
e
Application:
Give negations for each of the following statements:
a.The fan is slow or it is very hot.
b.Akram is unfit and Saleem is injured.
Solution
a.The fan is not slow and it is not very hot.
b.Akram is not unfit or Saleem is not injured.
INEQUALITIES AND DEMORGAN'S LAWS:
Use DeMorgan's Laws to write the negation of
-1 < x ≤ 4
Page 7
img
MTH001 ­ Elementary Mathematics
for some particular real no. x
-1 < x ≤ 4 means x > ­1 and x ≤ 4
By DeMorgan's Law, the negation is:
x > ­1 or x ≤ 4Which is equivalent to: x ≤ ­1 or x > 4
EXERCISE:
1. (p ∧ q) ∧ r ≡ p ∧(q ∧ r)
2. Are the statements (p∧q)∨r and p ∧ (q ∨ r) logically equivalent?
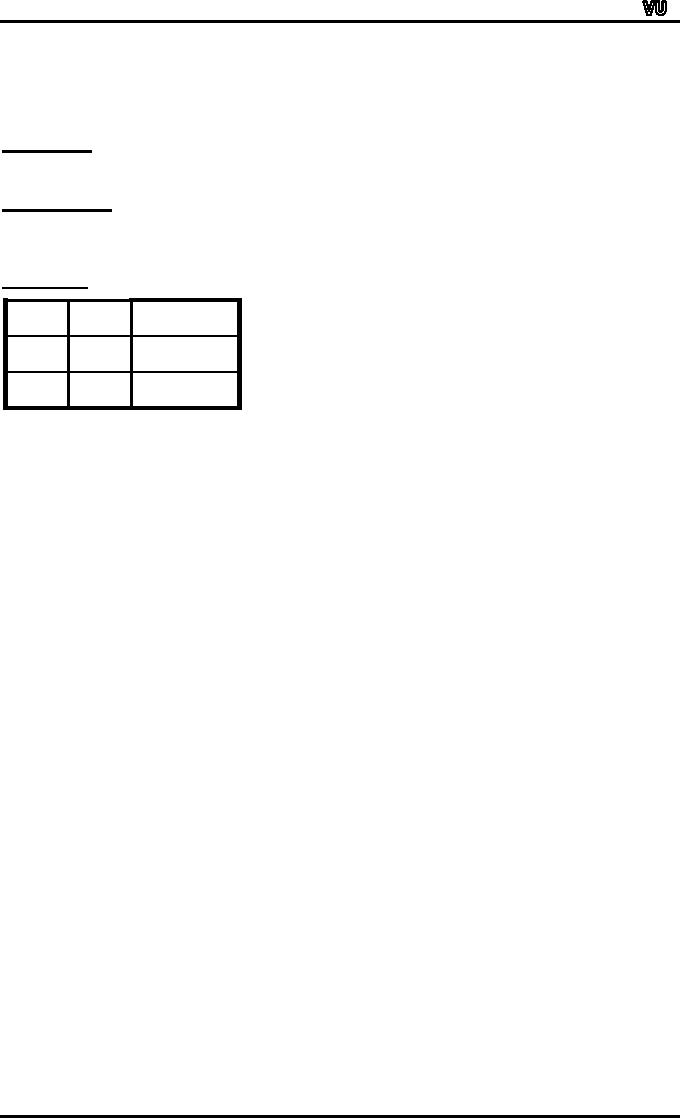
TAUTOLOGY:
A tautology is a statement form that is always true regardless of the truth
values of the statement variables.
A tautology is represented by the symbol "t"..
EXAMPLE:  The statement form p ∨ ~ p is tautology
p∨~p
p
~p
T
F
T
F
T
T
p ∨ ~p ≡ t
Page 8
Table of Contents:
  1. Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
  2. Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
  3. APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
  4. BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
  5. BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
  6. BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
  7. BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
  8. ORDERED PAIR:BINARY RELATION, BINARY RELATION
  9. REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
  10. REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
  11. RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
  12. INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
  13. SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
  14. SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
  15. Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
  16. Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
  17. Applications of Basic Mathematics Part 5:DECREASE IN RATE
  18. Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
  19. Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
  20. MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
  21. RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
  22. WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
  23. WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
  24. WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
  25. Median in Case of a Frequency Distribution of a Continuous Variable
  26. GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
  27. GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
  28. GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
  29. COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
  30. Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
  31. THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
  32. THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS