Applications of Basic Mathematics Part 5:DECREASE IN RATE

<< Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE

Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE >>

MTH001 Elementary Mathematics

LECTURE 17

Applications of Basic Mathematics

Part 5

OBJECTIVES

The objectives of the lecture are to learn about:

Discount

Simple and compound interest

Average due date, interest on drawings and calendar

REVISION LECTURE 5

A chartered bank is lowering the interest rate on its loans

from 9% to 7%.

What will be the percent decrease in the interest rate on a given

balance?

A chartered bank is increasing the interest rate on its loans from

7% to 9%

What will be the percent increase in the interest rate on a given

balance?

As we learnt in lecture 5, the calculation will be as follows:

Decrease in interest rate = 7-9 = -2 %

% decrease = -2/9 x 100 = -22.2 %

Increase in interest rate = 9-7 = 2 %

% decrease = 2/7 x 100 = 28.6 %

The calculations in Excel are shown in the following slides:

DECREASE IN RATE

Data entry

Cell F4 = 9

Cell F5 = 7

Formulas

Formula for decrease in Cell F6: = =F5-F4

Formula for % decrease in Cell F7: =F6/F4*100

Results

Cell F6 = -2%

Cell F7 = -22.2%

INCREASE IN RATE

Data entry

Cell F14 = 7

Cell F15 = 9

Formulas

Formula for increase in Cell F16: =F15-F14

Formula for % increase in Cell F17: =F16/F14*100

Results

Cell F16 = 2%

Cell F17= 28.6%

Page

111

MTH001 Elementary Mathematics

The Definition of a Stock

Plain and simple, stock is a share in the ownership of a company. Stock

represents a claim on the company's assets and earnings. As you acquire more

Page

112

MTH001 Elementary Mathematics

stock, your ownership stake in the company becomes greater. Whether you say

shares, equity, or stock, it all means the same thing.

Stock yield

With stocks, yield can refer to the rate of income generated from a stock in the form

of regular dividends. This is often represented in percentage form, calculated as the

annual dividend payments divided by the stock's current share price.

Earnings per share (EPS)

The EPS is the total profits of a company divided by the number of shares. A company with

$1 billion in earnings and 200 million shares would have earnings of $5 per share.

Price-earnings ratio

A valuation ratio of a company's current share price compared to its per-share earnings.

Calculated as:

For example, if a company is currently trading at $43 a share and earnings over the

last 12 months were $1.95 per share, the P/E ratio for the stock would be 22.05

($43/$1.95).

Outstanding shares

Stock currently held by investors, including restricted shares owned by the

company's officers and insiders, as well as those held by the public. Shares that have

been repurchased by the company are not considered outstanding stock.

Net current asset value per share(NCAVPS)

NCAVPS is calculated by taking a company's current assets and subtracting the total

liabilities, and then dividing the result by the total number of shares outstanding.

Current Assets

The value of all assets that are reasonably expected to be converted into cash within one

year in the normal course of business. Current assets include cash, accounts receivable,

inventory, marketable securities, prepaid expenses and other liquid assets that can be

readily converted to cash.

Liabilities

A company's legal debts or obligations that arise during the course of business operations.

Market value

The price at which investors buy or sell a share of stock at a given time

Face value

Page

113

MTH001 Elementary Mathematics

Original cost of a share of stock which is shown on the certificate. Also referred to as "par

value."

Face value is usually a very small amount that bears no relationship to its market price.

Dividend

Usually, a company distributes a part of the profit it earns as dividend.

For example: A company may have earned a profit of Rs 1 crore in 2003-04. It

keeps half that amount within the company. This will be utilised on buying new

machinery or more raw materials or even to reduce its borrowing from the bank.

It distributes the other half as dividend.

Assume that the capital of this company is divided into 10,000 shares. That

would mean half the profit -- ie Rs 50 lakh (Rs 5 million) -- would be divided by

10,000 shares; each share would earn Rs 500. The dividend would then be Rs

500 per share. If you own 100 shares of the company, you will get a cheque of

Rs 50,000 (100 shares x Rs 500) from the company.

Sometimes, the dividend is given as a percentage -- i e the company says it has

declared a dividend of 50 percent. It's important to remember that this dividend is

a percentage of the share's face value. This means, if the face value of your

share is Rs 10, a 50 percent dividend will mean a dividend of Rs 5 per share

BUYING SHARES

If you buy 100 shares at Rs. 62.50 per share with a 2% commission, calculate

your total cost.

Calculation

100 * Rs. 62.50 = Rs. 6,250

0.02 * Rs. 6,250 =

125

Total

= Rs. 6,375

RETURN ON INVESTMENT

Suppose you bought 100 shares at Rs. 52.25 and sold them after 1 year at Rs.

68. With a 1% commission rate of buying and selling the stock and 10 %

dividend per share is due on these shares. Face value of each share is 10Rs.

What is your return on investment?

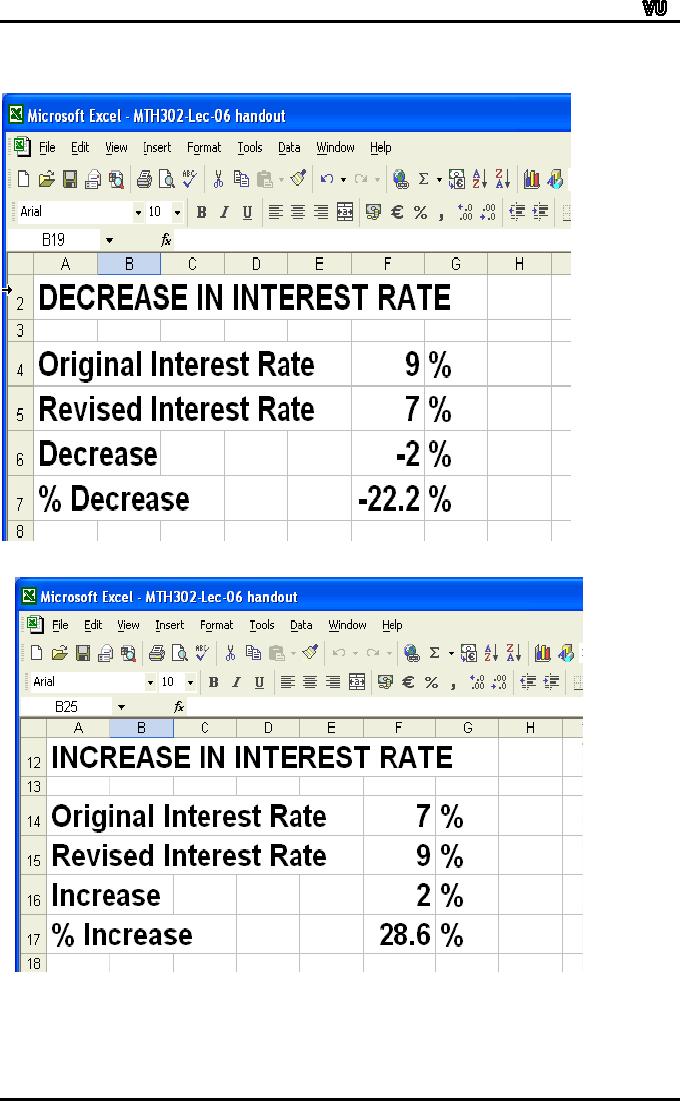
Bought

Page

114

MTH001 Elementary Mathematics

100 shares at Rs. 52.25 = 5,225.00

Commission at 1%

52.25

Total Costs

=5,225 + 52.25 = 5,277.25

Sold

100 shares at Rs. 68

= 6,800.00

Commission at 1%

= - 68.00

Total Costs Sale

= 6,800 68 = 6,732.00

Gain

Net receipts

= 6,732.00

Total cost

= - 5,277.25

Net Gain

= 6,732 5,277.25 =1,454.75

Dividends (100*10/10)

= 100.00

Total Gain

= 1,454.75 + 100 = 1,554.75

Return on investment

= 1,554.75/5,277.25*100

= 29.46 %

The calculations using Excel were made as follows:

BOUGHT

Data entry

Cell B21: 100

Cell B22: 52.25

Formulas

Formula for Cost of 100 shares at Rs. 52.25 in Cell B23: =B21*B22

Formula for Commission at 1% in Cell B24: =B23*0.01

Formula for Total Costs in Cell B25: =B23+B24

Results

Cell B23 = 5225

Cell B24 = 52.25

Cell B25 = 5277.25

Page

115

MTH001 Elementary Mathematics

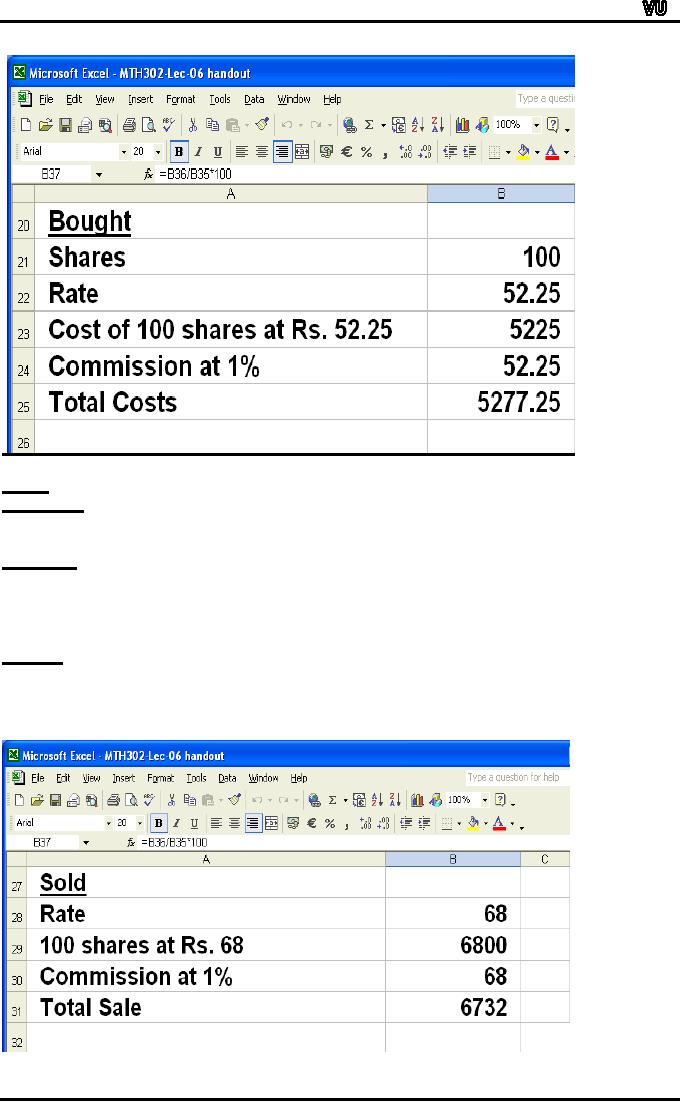
SOLD

Data entry

Cell B28: 68

Formulas

Formula for sale of 100 shares at Rs. 68 in Cell B29: =B21*B28

Formula for Commission at 1% in Cell B30: =B29*0.01

Formula for Total Sale in Cell B31: =B29-B30

Results

Cell B29 = 6800

Cell B30 = 68

Cell B31 = 6732

Page

116

MTH001 Elementary Mathematics

GAIN

Formulas

Formula for Net receipts in Cell B34: =B31

Formula for Total cost in Cell B35: =B25

Formula for Net Gain in Cell B36: =B31-B25

Formula for % Gain in Cell B37: =B36/B35*100

Results

Cell B34 = 6732

Cell B35 = 5277.25

Cell B36 = 1454.75

Cell B37 = 27.57

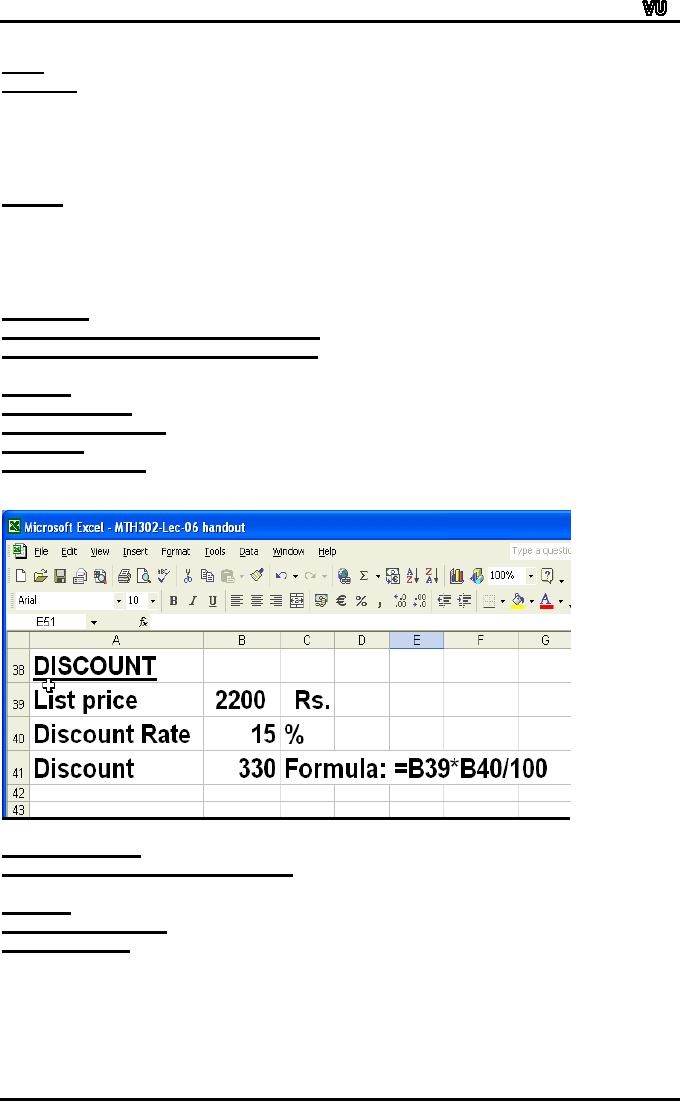
DISCOUNT

Discount is Rebate or reduction in price.

Discount is expressed as % of list price.

Example

List price = 2200

Discount Rate = 15%

Discount?

= 2200 x 0.15= 330

Calculation using Excel along with formula is given in the following slide:

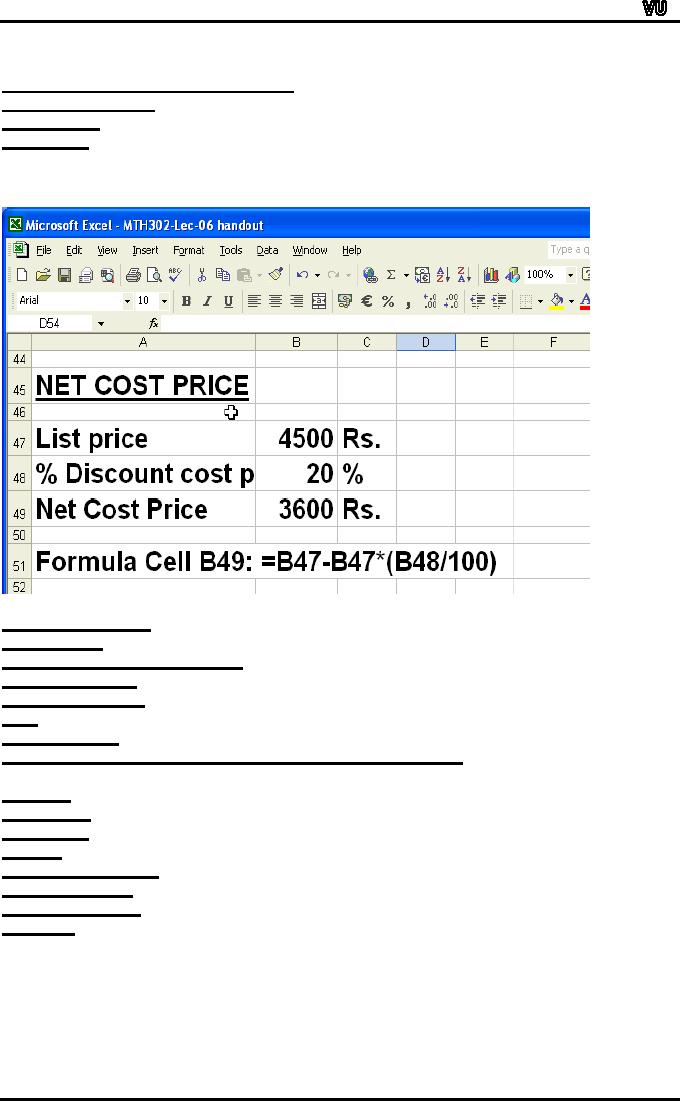
NET COST PRICE

Net Cost Price = List price - Discount

Example

List price = 4,500 Rs.

Discount = 20 %

Netcost price?

Page

117

MTH001 Elementary Mathematics

Net cost price = 4,500 20 % of 4,500

= 4,500 0.2 x4,500

=4,500 900

= 3,600 Rs.

Calculation using Excel along with formula is given in the following slide:

SIMPLE INTEREST

P = Principal

R = Rate of interest per annum

T = Time in years

I = Simple interest

then

I = P. R. T / 100

Thus total amount A to be paid at the end of T years = P + I

Example

P = Rs. 500

T = 4 years

R =11%

Find simple interest

I = P x T x R /100

= 500 x 4 x 11/100

= Rs. 220

Calculation using Excel along with formula is given in the following slide:

Page

118

MTH001 Elementary Mathematics

COMPOUND INTEREST

Compound Interest also attracts interest.

Example

P = 800

Interest year 1= 0.1 x 800= 80

New P = 800 + 80 = 880

Interest on 880 = 0.1 X 880 = 88

New P = 880 + 88 = 968

Calculation using Excel along with formula is given in the following slide:

Page

119

MTH001 Elementary Mathematics

mpound Interest Formula

S = Money accrued after n years also called compound amount

P = Principal

r = Rate of interest

n = Number of periods

S = P(1 + r/100)^ n

Compound interest = S - P

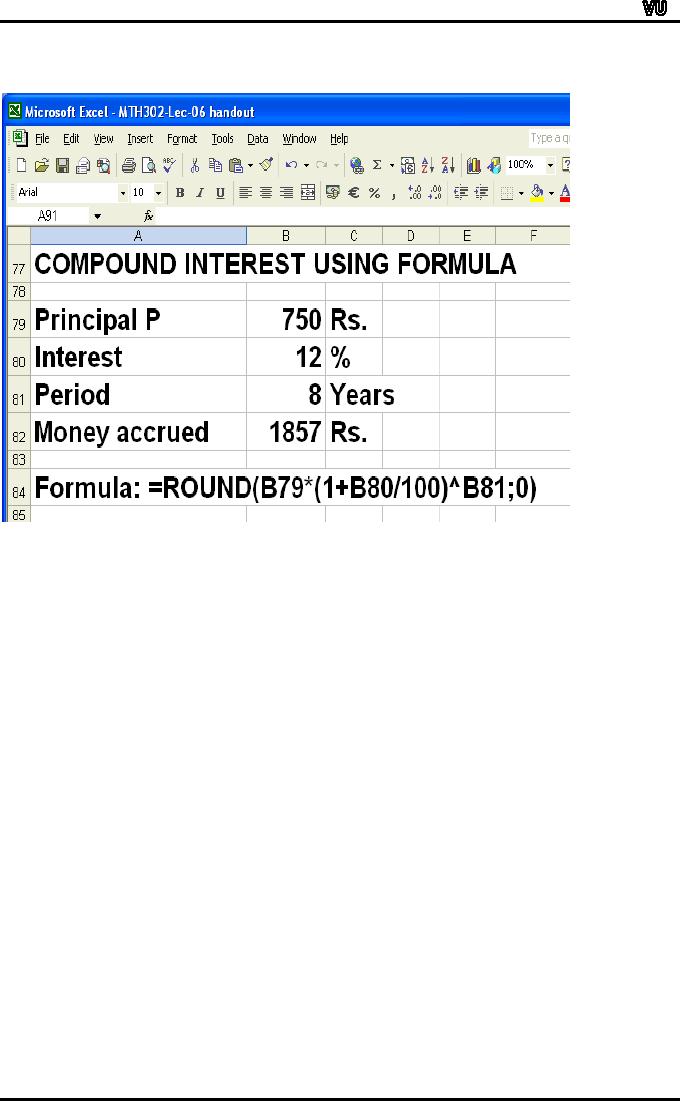
Example

Calculate compound interest earned on Rs. 750 invested at 12% per annum for

8 years.

S= P(1+r/100)^8

= 750(1+12/100)^8

=1857 Rs

Compound interest = 1857 750 = 1107 Rs

Page

120

MTH001 Elementary Mathematics

Calculation using Excel along with formula is given in the following

slide

Page

121

Table of Contents: