 |
Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE |
| << Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS |
| Applications of Basic Mathematics Part 5:DECREASE IN RATE >> |
MTH001
Elementary Mathematics
LECTURE #
16
Applications of
Basic Mathematics
Part
4
OBJECTIVES
The
objectives of the lecture
are to learn about:
�
Basic
calculations of percentages, salaries
and investments
using
Microsoft
Excel
PERCENTAGE
CHANGE
Monday's
Sales were Rs.1000 and
grew to Rs. 2500 the
next day.
Find
the percent
change.
METHOD
Change
= Final value initial
value
Percentage
change = (Change / initial
value) x 100%
CALCULATION
Initial
value =1000
Final
value = 2500
Change
=
1500
%
Change = (1500/1000) x 100 =
150%
The
calculations using Excel are
given below.
First
the entries of data were
made as follows:
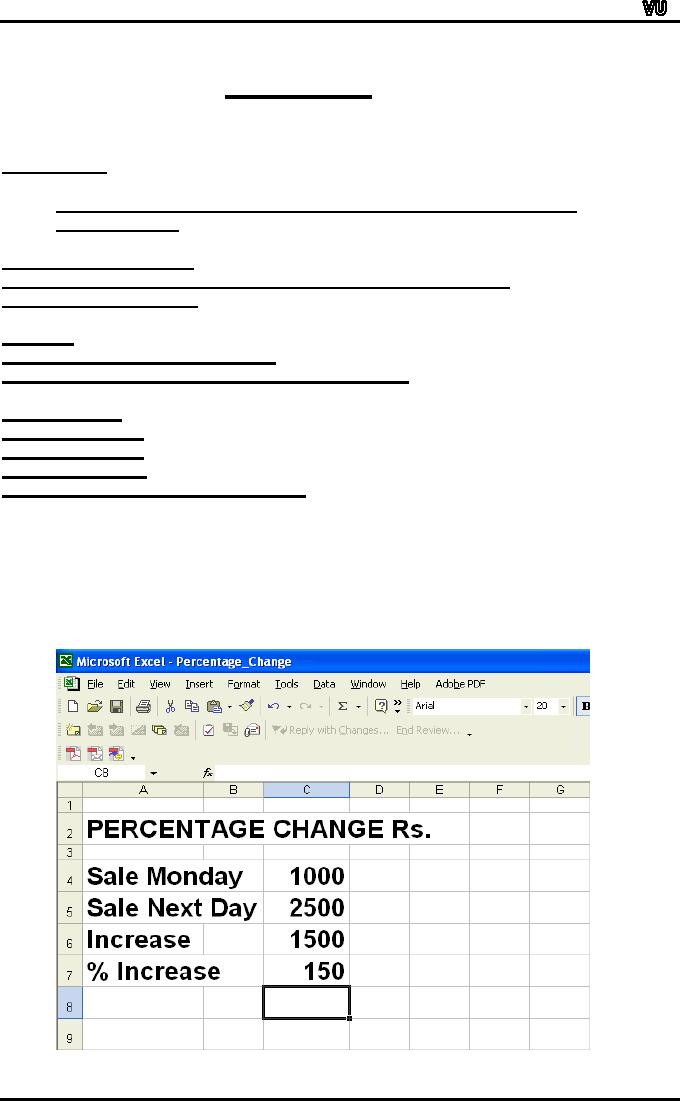
Cell
C4 = 1000
Cell
C5 = 2500
In
cell C6 the formula for
increase was: = C5 C4
The
result was 1500.
In
cell C7 the formula for
percentage change was: =
C6/C4*100
The
result 150 is shown in the
next slide.
Page
102
MTH001
Elementary Mathematics
EXAMPLE
1
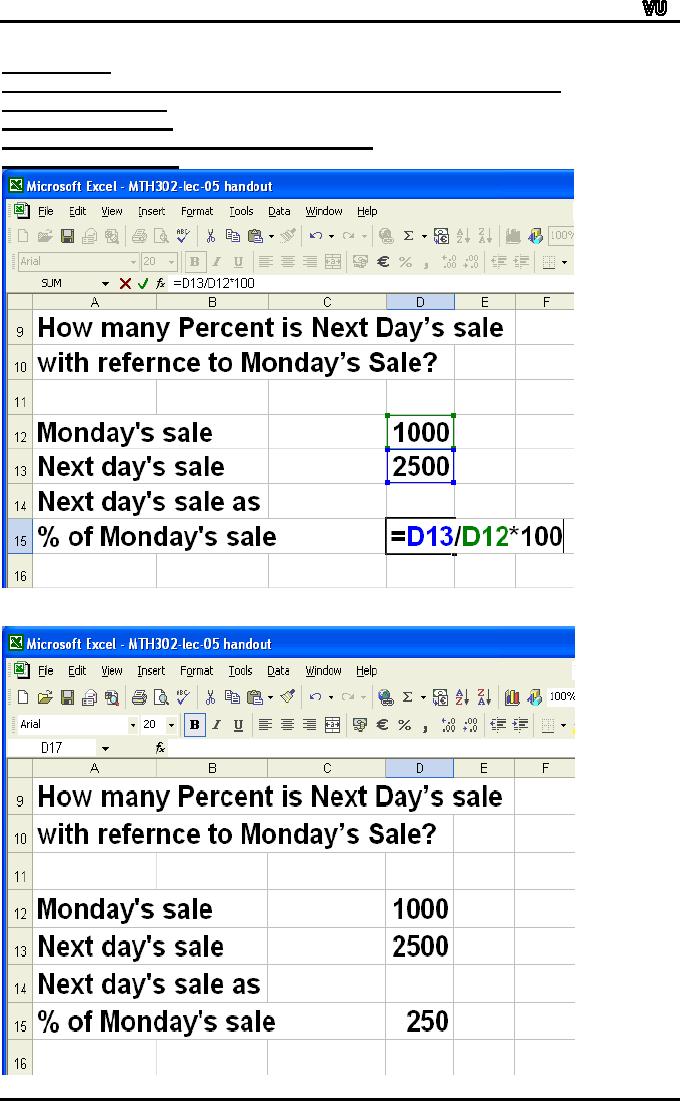
How
many Percent is Next Day's
sale with reference to
Monday's Sale?
Monday's
sale= 1000
Next
day's sale= 2500
Next
day's sale as % = 2500/1000 x
100 = 250 %
=
Two and a half
times
Page
103
MTH001
Elementary Mathematics
EXAMPLE
2
In
the making of dried fruit,
15kg. of fresh fruit shrinks
to 3 kg of dried fruit.
Find
the percentage
change.
Calculation
Original
fruit = 15 kg
Final
fruit = 3 kg
Change
= 3-15 = -12
%
change = - 12/15 x 100 = - 80
%
Size
was reduced by 80%
Page
104

MTH001
Elementary Mathematics
Calculations
in Excel were done as
follows:
Data
entry
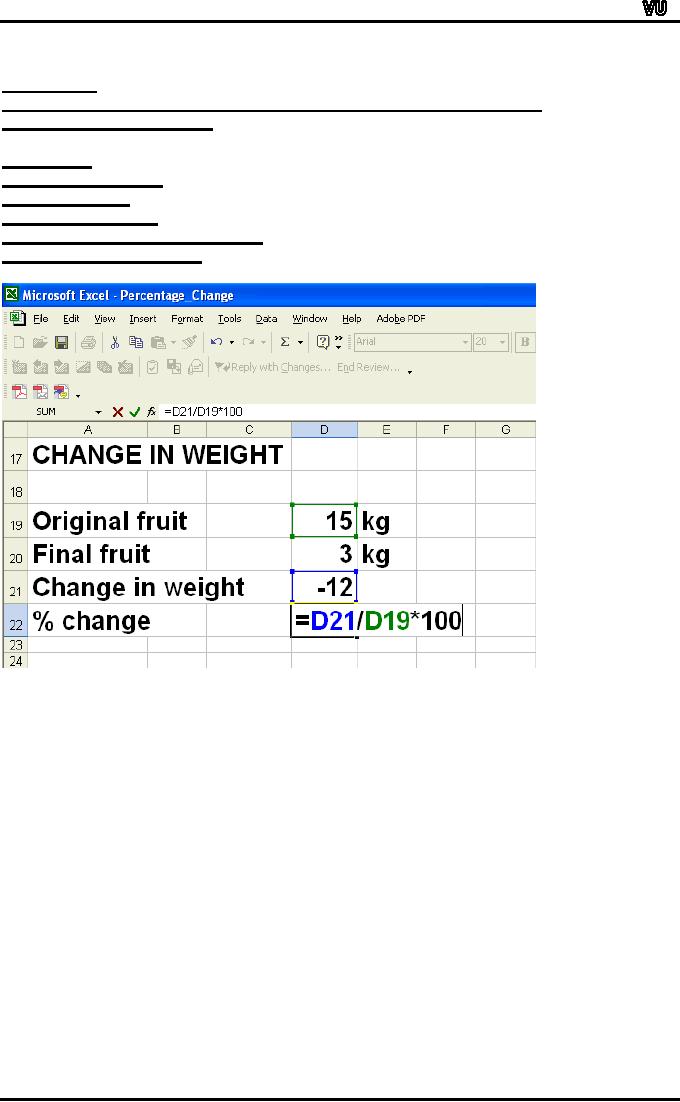
Cell
D19: 15
Cell
D20: 3
Formulas
Formula
for change in Cell D21: =
D20 D19
Formula
for %change in Cell D22: =
D21/D19*100
Results
Cell
D21 = -12 kg
Cell
D22 = -80 %
EXAMPLE
3
After
mixing with water the
weight of cotton increased
from 3 kg to 15 kg.
Find
the
percentage change.
CALCULATION
Original
weight = 3 kg
Final
weight = 15 kg
Change
= 15-3= 12
%
change = 12/3 x 100 = 400
%
Weight
increased by 400%
Page
105

MTH001
Elementary Mathematics
Calculations
in Excel were done as
follows:
Data
entry
Cell
D26: 3
Cell
D27: 15
Formulas
Formula
for change in Cell D28: =
D27 D26
Formula
for %change in Cell D29: =
D28/D26*100
Results
Cell
D28 = 12 kg
Cell
D29 = 400 %
EXAMPLE
4
A
union signed a three year
collective agreement that
provided for wage
increases
of 3%, 2%, and 1% in
successive years
An
employee is currently earning
5000 rupees per
month
What
will be the salary per
month at the end of the
term of the
contract?
Calculation
=
5000(1 + 3%)(1 + 2%)(1 +
1%)
=
5000 x 1.03 x 1.02 x
1.01
=
5306 Rs.
Calculations
using Excel are shown in
the following slides.
Page
106

MTH001
Elementary Mathematics
Page
107
MTH001
Elementary Mathematics
Calculations
in Excel were done as
follows:
Page
108
MTH001
Elementary Mathematics
Data
entry
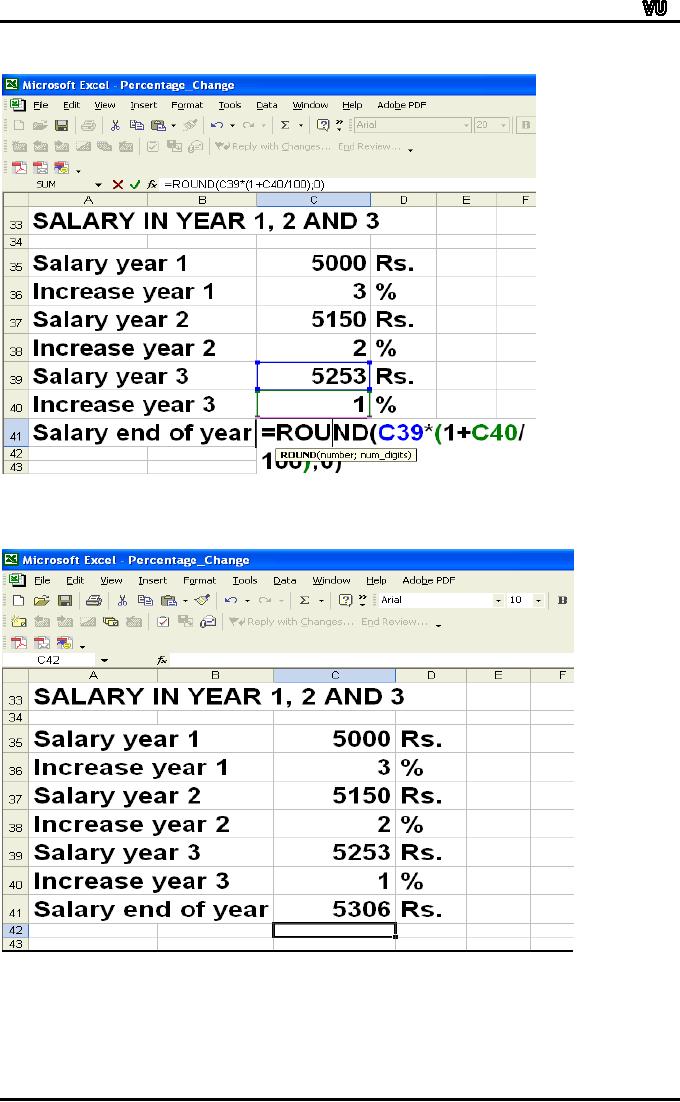
Cell
C35: 5000
Cell
C36: 3
Cell
C38: 2
Cell
C40: 1
Formulas
Formula
for salary in year 2 in Cell
C37: =ROUND(C35*(1+C36/100);0)
Formula
for salary year 3 in Cell
C39: =ROUND(C37*(1+C38/100);0)
Formula
for salary at the end of
year 3 in Cell C41:
=ROUND(C35
C39*(1+C39/100);0)
Results
Cell
C37 = 5150 Rs.
Cell
C39 = 5253 Rs.
Cell
C41= 5306 Rs.
EXAMPLE
5
An
investment has been made
for a period of 4
years.
Rates
of return for each year
are 4%, 8%, -10%
and 9% respectively.
If
you invested Rs. 100,000 at
the beginning of the term,
how much will you
have
at
the end of the last
year?
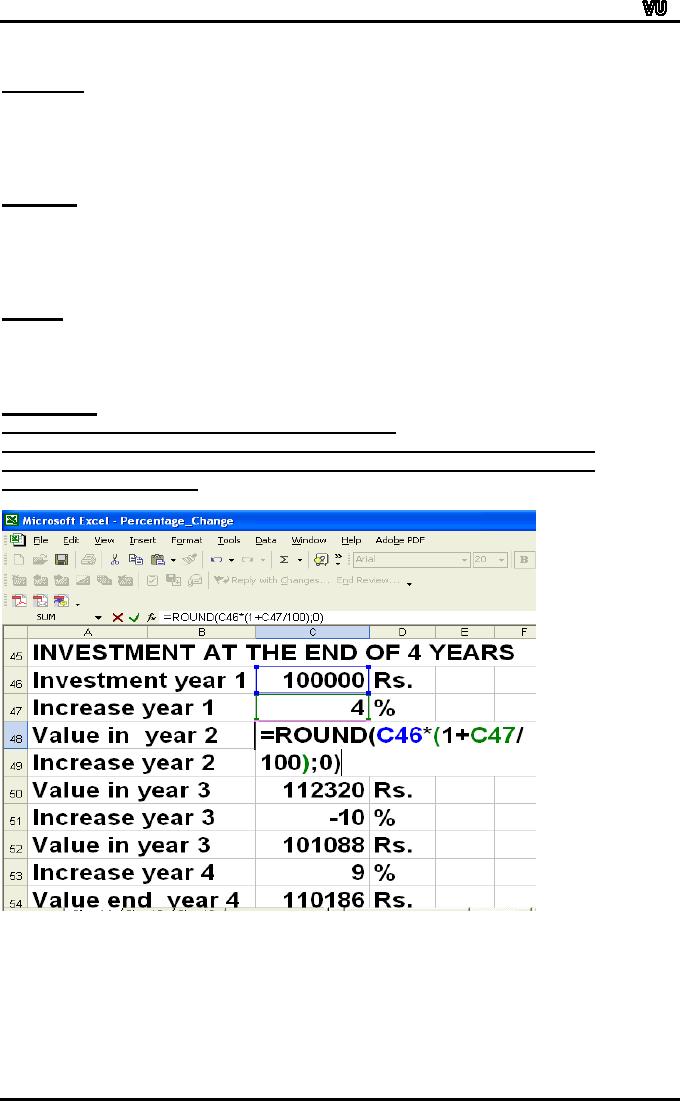
Page
109

MTH001
Elementary Mathematics
Calculations
in Excel were done as
follows:
Data
entry
Cell
C46: 100000
Cell
C47: 4
Cell
C49: 8
Cell
C51: -10
Cell
C53: 9
Formulas
Formula
for value in year 2 in Cell
C48: = ROUND(C46*(1+C47/100);0)
Formula
for value in year 3 in Cell
C50: = ROUND(C48*(1+C49/100);0)
Formula
for value in year 4 in Cell
C52: = ROUND(C50*(1+C51/100);0)
Formula
for salary end of year 4 in
Cell C54: =
ROUND(C52*(1+C53/100);0)
Results
Cell
C48 = 104000 Rs.
Cell
C50 = 112320 Rs.
Cell
C52 = 101088 Rs.
Cell
C54 = 110186Rs.
Page
110
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS