 |
INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO |
| << RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS |
| SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE: >> |
MTH001
Elementary Mathematics
LECTURE #
12
INJECTIVE
FUNCTION
or
ONE-TO-ONE
FUNCTION
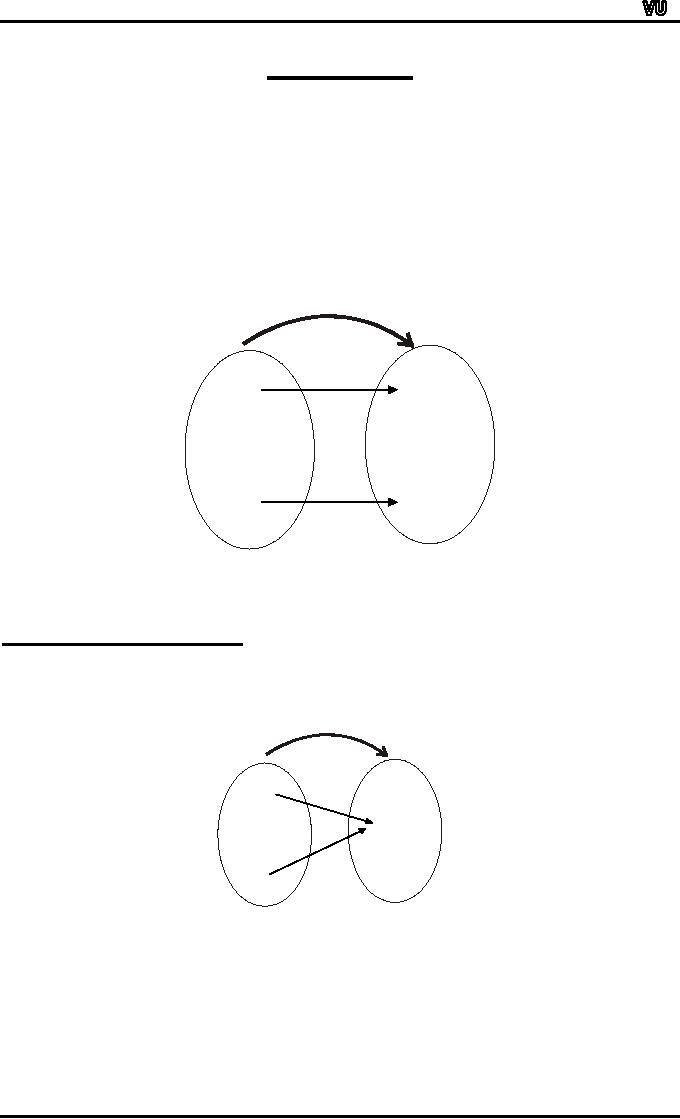
Let
f: X →Y
be a function. f is injective or
one-to-one if, and only
if, ∀
x1,
x2
∈X,
if x1 ≠ x2 then
f(x1) ≠
f(x2)That
is, f is one-to-one if it maps
distinct
points
of the domain into the
distinct points of the
co-domain.
f
f(x1)
x1
x2
f(x2)
A
one-to-one function separates
points.
FUNCTION
NOT ONE-TO-ONE:
A
function f: X →Y is not
one-to-one iff there exist
elements x1 and
x2 in such
that
x1 ≠ x2 but f(x1) =
f(x2).That is, if
distinct elements x1 and x2
can
found in
domain
of f that have the same
function value.
f
x1
f(x1)=f(x2)
Y=co-domain
of f
X=domain
of f
x2
A
function that is not
one-to-one collapses points
together.
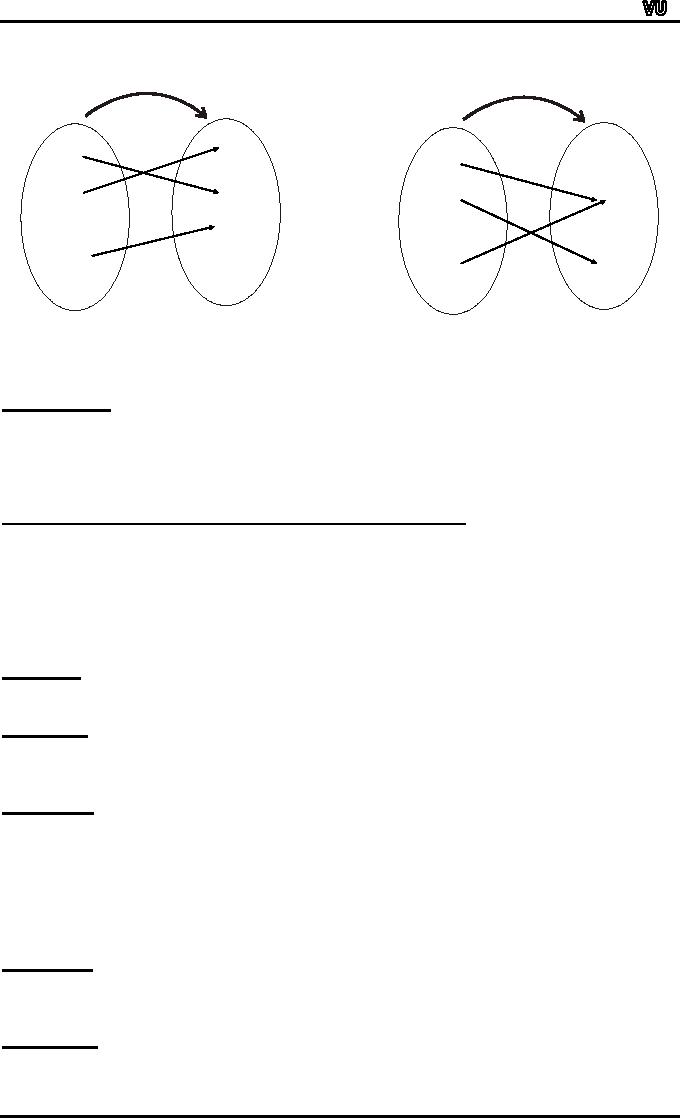
EXAMPLE:
Which
of the arrow diagrams define
one-to-one functions?
Page
68
MTH001
Elementary Mathematics
f
g
1
1
a
a
2
2
b
b
3
3
c
c
4
4
X
X
Y
Y
SOLUTION:
f
is clearly one-to-one function,
because no two different
elements of Xare
mapped
onto the same element of
Y.
g
is not one-to-one because
the elements a and c are
mapped onto the
same
element
2 of Y.
ALTERNATIVE
DEFINITION FOR ONE-TO-ONE
FUNCTION:
A
function f: X →Y is one-to-one
(1-1) iff ∀
x
1, x2
∈X, if x1 ≠
x2 then f(x1)
≠
f(x2 )
(i.e
distinct elements of 1st set have their
distinct images in 2nd set)
The
equivalent contra-positive statement
for this implication is∀
x1,
x2 ∈X,
if
f(x1 )
= f(x2),
then x1
= x2
REMARK:
f:
X →Y
is not one-to-one iff ∃
x1,
x2 ∈X with
f(x1) = f(x2) but x1 ≠
x2
EXAMPLE:
Define
f: R →R
by the rule f(x) = 4x - 1
for all x ∈R
Is
f one-to-one? Prove or give a
counter example.
SOLUTION:
Let
x1,
x2 ∈R such
that f(x1) =
f(x2)
⇒
4x1 - 1 = 4
x2 1
(by
definition of f)
⇒
4
x1 = 4 x2
(adding
1 to both sides)
⇒
x1 =
x2 (dividing both sides by
4)
Thus
we have shown that if
f(x1) = f(x2)
then x1=x2
Therefore,
f is one-to-one
EXAMPLE:
Define
g : Z → Z by the
rule g(n)=n2 for all n ∈Z
Is
g one-to-one? Prove or give a
counter example.
SOLUTION:
Let
n1,
n2 ∈Z and
suppose g(n1) =
g(n2)
Page
69
MTH001
Elementary Mathematics
n12 =
n22
⇒
(by
definition of g)
⇒
either
n1 =
+ n2 or n1 = -
n2
Thus
g(n1)
= g(n2)
does not imply n1 =
n2 always.
As
a counter example, let
n1 =
2 and n2
=
-2.
Then
g(n1) =
g(2) = 22
= 4
and
also g(n2)
= g(-2) = (-2) 2 =
4
Hence
g(2) = g(-2) where as 2 ≠-2
and so g is not
one-to-one.
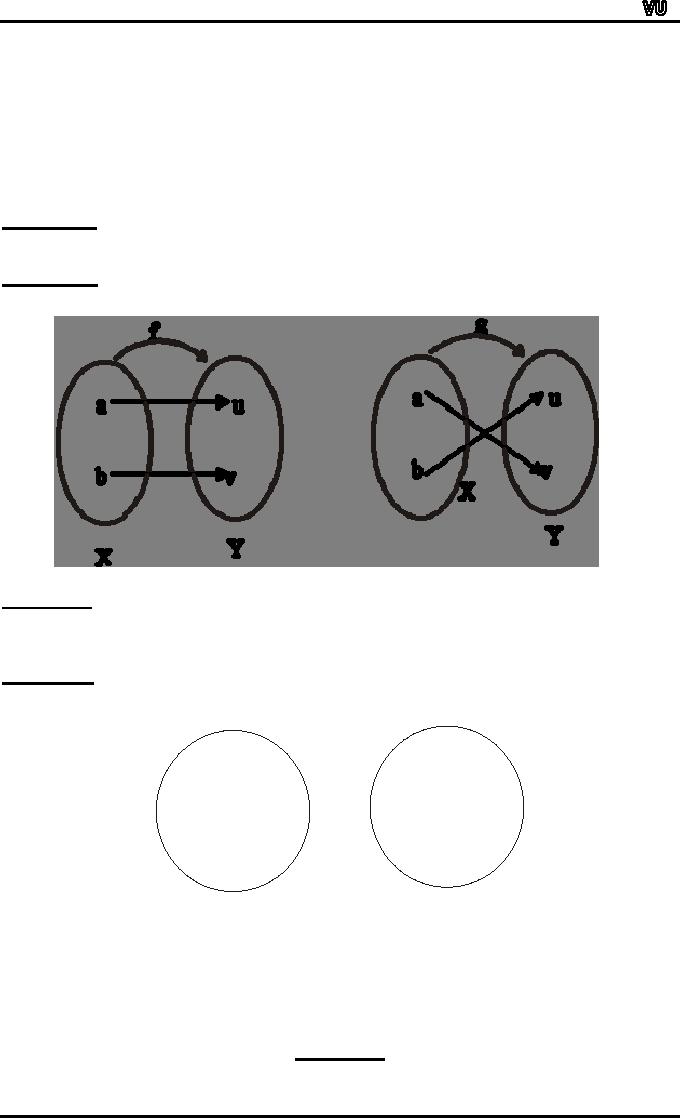
EXERCISE:
Find
all one-to-one functions
from X = {a,b} to Y =
{u,v}
SOLUTION:
There
are two one-to-one functions
from X to Y defined by the
arrow diagrams.
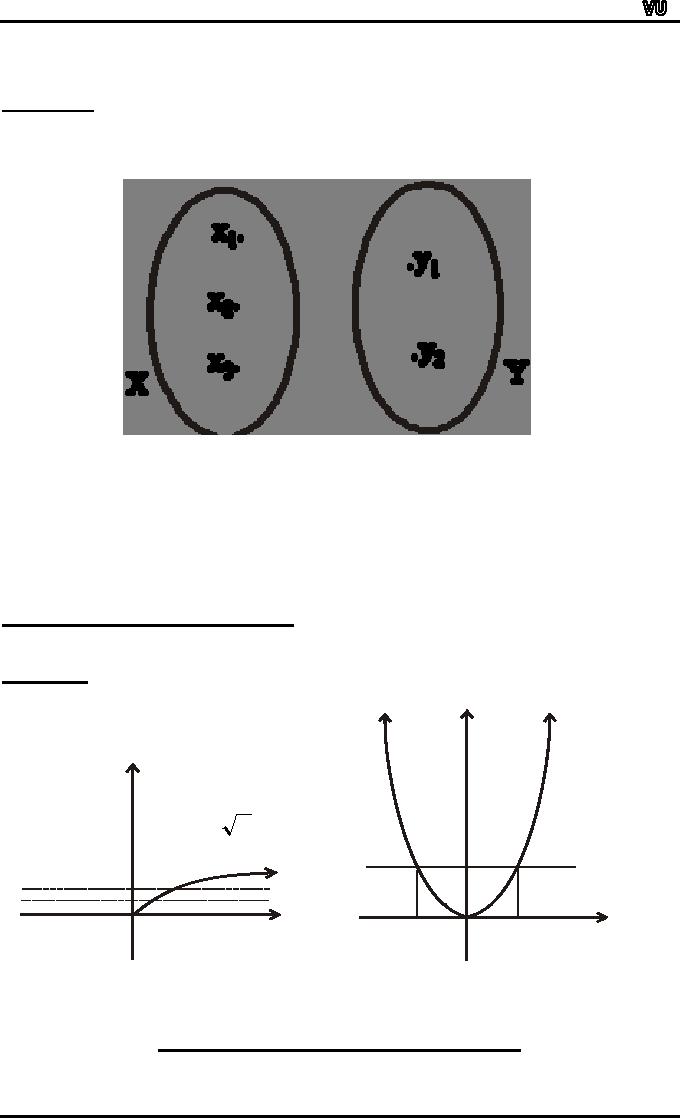
EXERCISE:
How
many one-to-one functions are
there from a set with
three elements to
a
set with four
elements.
SOLUTION:
Let
X = { x 1,x
2, x 3}
and Y = {y 1,y
2,y 3,y
4}
x
1.
.y
1
x
2.
.y
2
.y
3
x
3.
.y
4
X
Y
x1 may be mapped to any of
the 4 elements of Y. Then x2 may be mapped to any of
the
remaining
3 elements of Y & finally x3 may be mapped to any of
the remaining 2
elements
of
Y.
Hence,
total no. of one-to-one
functions from X to Y
are
4
� 3 � 2 = 24
EXERCISE:
Page
70
MTH001
Elementary Mathematics
How
many one-to-one functions
are there from a set
with three elements to a set
with two
elements.
SOLUTION:
Let
X = {x 1, x
2, x 3}
and Y = {y 1, y
2}
Two
elements in X could be mapped to
the two elements in Y
separately. But there is
no
new
element in Y to which the
third element in X could be
mapped. Accordingly there is
no
one-to-one
function from a set with
three elements to a set with
two elements.
GRAPH
OF ONE-TO-ONE FUNCTION:
A
graph of a function f is one-to-one
iff every horizontal line
intersects the graph in at
most
one
point.
EXAMPLE:
y
y=x2
y
y=
x
(
- 2 ,4 )
(
2 ,4 )
0
0
x
-2
+2
x
O
N E -T O -O N E F U N C T IO N
N
O T O N E -T O -O N E F U N C T IO N
fro
m R + to
R
F
ro m R to R +
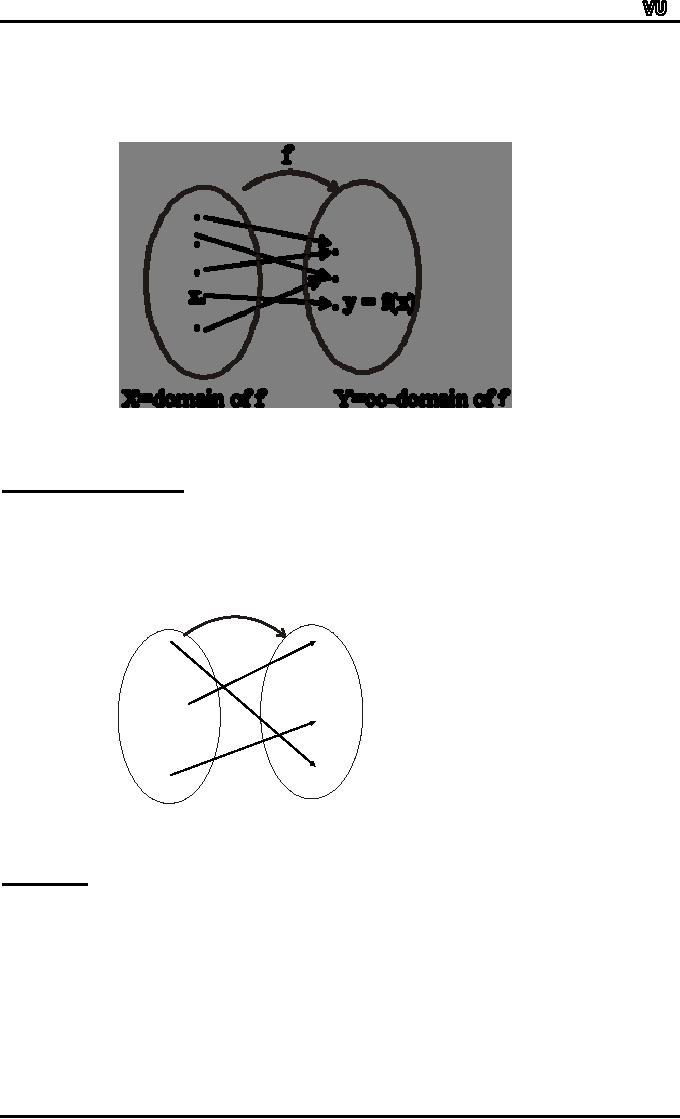
SURJECTIVE
FUNCTION or ONTO
FUNCTION:
Page
71
MTH001
Elementary Mathematics
Let
f: X→Y
be a function. f is surjective or onto
if, and only if,
"∀
y ε Y, ∃
x εX
such that f(x) =
y.
That
is, f is onto if every
element of its co-domain is
the image of some element(s)
of its
domain.i.e.,
co-domain of f = range of f
Each
element y in Y equals f(x)
for at least one x in
X
FUNCTION
NOT ONTO:
A
function f:X→Y is not
onto iff there exists
yε
Y
such that ∀x εX, f(x)
≠y.
That
is, there is some element in
Y that is not the image of
any element in X.
f
.
.
.
.
.
.
.
X=
domain of f
Y=co-do
mai n of f
.
EXAMPLE:
Which
of the arrow diagrams define
onto functions?
Page
72
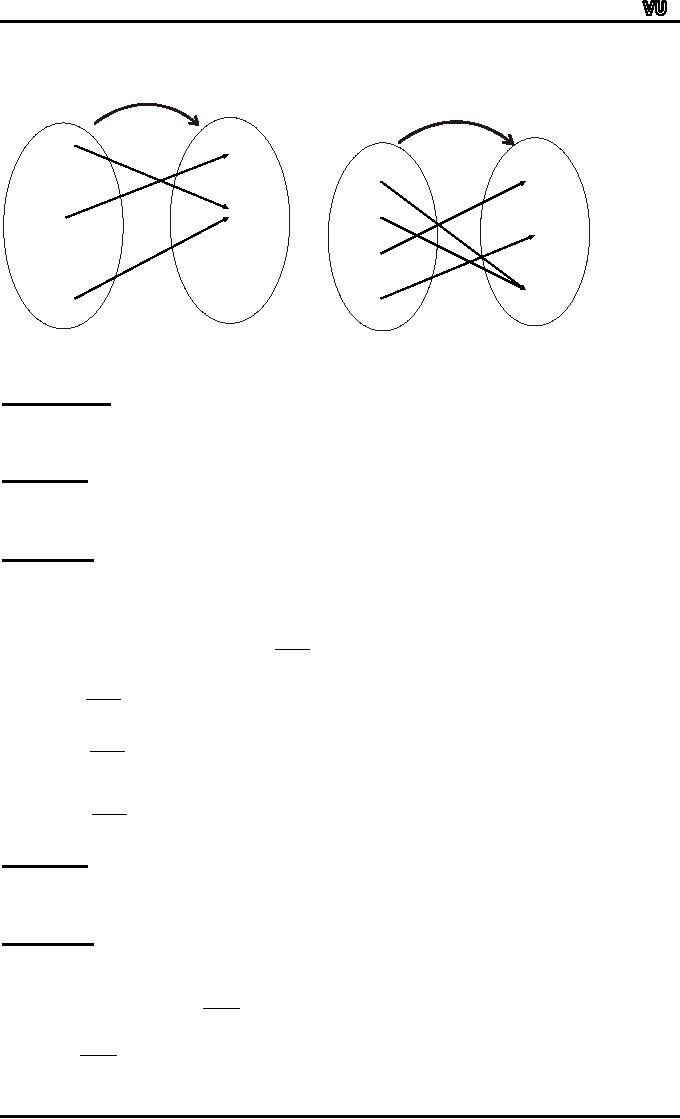
MTH001
Elementary Mathematics
f
g
a
1
a
1
2
b
b
2
c
d
.3
3
c
Y
Y
X
X
SOLUTION:
f
is not onto because 3 ≠
f(x)
for any x in X. g is clearly
onto because each element of
Y
equals
g(x) for some x in X.
as
1 = g(c);,2 = g(d);3 = g(a) =
g(b)
EXAMPLE:
Define
f: R →R
by the rule
for
all x ∈R
f(x)
= 4x-1
Is
f onto? Prove or give a
counter example.
SOLUTION:
Let
y ∈R.
We search for an x ∈
R
such that
f(x)
= y
or
4x-1
= y
(by
definition of f)
y
+1
x=
∈
R
. Hence
for every y ∈R,
there
Solving
it for x, we find
x=y+1
4
y
+1
exists
such
that
x=
∈R
4
⎛
y
+1⎞
f
(
x)
=
f
⎜
⎟
⎝ 4 ⎠
⎛
y
+1⎞
=
4.⎜
⎟
- 1
=
(
y
+
1)
-
1
=
y
⎝ 4 ⎠
Hence
f is onto.
EXAMPLE:
Define
h: Z →Z
by the rule
h(n)
= 4n - 1 for all n ∈
Z
Is
h onto? Prove or give a
counter example.
SOLUTION:
Let
m ∈Z.
We search for an n ∈Z such
that h(n) = m.
or
4n
- 1 = m
(by
definition of h)
m
+1
Solving
it for n, we find n
=
4
m
+1
n=
is
not always an integer for
all m ∈Z.
But
4
Page
73
MTH001
Elementary Mathematics
As
a counter
example, let m =
0∈
Z,
then
h(n)
= 0
⇒
4n-1
= 0
⇒
4n
= 1
1
n
=
∉Ζ
⇒
4
Hence
there is no integer n for
which h(n) = 0.
Accordingly,
h is not onto.
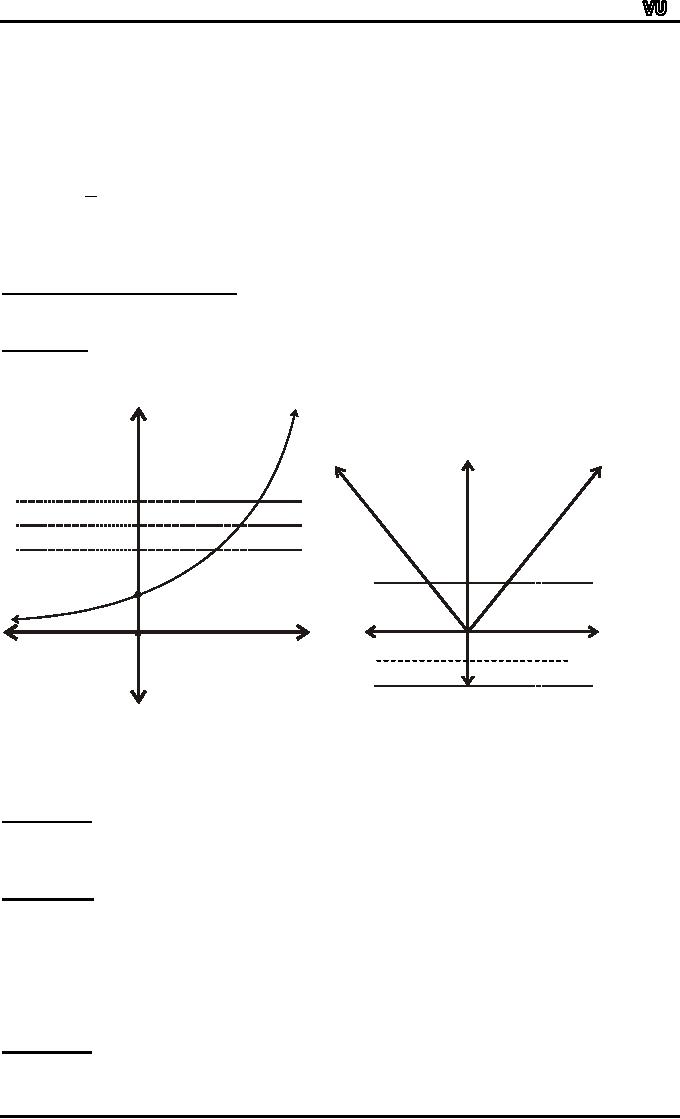
GRAPH
OF ONTO FUNCTION:
A
graph of a function f is onto
iff every horizontal line
intersects the graph in at
least one
point.
EXAMPLE:
y
y=ex
y
= |x|
y
x
O
O
x
NOT
ONTO FUNC TION FROM
ONTO
FUNC TION
from
R to R+
R
to R
EXERCISE:
Let
X = {1,5,9} and Y = {3,4,7}.Define g: X
→Y
by specifying that
g(1)
= 7,
g(5)
= 3,
g(9)
= 4
Is
g one-to-one? Is g onto?
SOLUTION:
g
is one-to-one because each of
the three elements of X are
mapped to a different
elements
of
Y by g.
g(1)
≠
g(5),
g(1)
≠
g(a),
g(5)
≠
g(a)
g
is onto as well, because
each of the three elements
of co-domain Y of g is the image
of
some
element of the domain of
g.
3
= g(5),
4
= g(9),
7
= g(1)
EXERCISE:
Define
f: P({a,b,c})→Z as
follows:
Page
74
MTH001
Elementary Mathematics
for
all A∈P ({a,b,c}),
f(A)= the number of elements
in A.
a.
Is f one-to-one? Justify.
b.
Is f onto? Justify.
SOLUTION:
f
is not one-to-one because
f({a}) = 1 and f({b}) = 1
but {a}≠
{b}
a.
b.
f
is not onto because, there
is no element of P({a,b,c}) that is
mapped
to
4 ∈Z.
EXERCISE:
Determine
if each of the functions is
injective or surjective.
f:
Z →Z+
define as f(x) = |x|
a.
g:
Z+ →
Z+ � Z+ defined as
g(x) = (x,x+1)
b.
SOLUTION:
a.
f
is not injective,
because
f(1)
= |1| = 1 and
f(-1)
= |-1| = 1
1
≠
-1
i.e.,
f(1)
= f(-1)
but
f
is onto, because
for every a∈Z+,
there exist a and +a in Z
such that
f(-a)
= |-a| = a and f(a) =
|a| = a
g:
Z+ →
Z+ � Z+ defined as
g(x) = (x,x+1)
b.
g(x1)
= g(x2) for x1, x2 ∈Z+
Let
⇒
(x1,
x1 +1) = (x2, x2+1)
(by
definition of g)
⇒
x1
= x2 and x1 + 1 = x2 + 1
(by
equality of ordered
pairs)
⇒
x1
= x2
Thus
if g(x1) = g(x2) then x1 =
x2
Hence
g is
one-to-one.
g
is not onto because
(1,1) ∈Z+�Z+ is not
the image of any element of
Z+.
BIJECTIVE
FUNCTION
or
ONE-TO-ONE
CORRESPONDENCE
A
function f: X→Y that is
both one-to-one (injective)
and onto (surjective) is
called a bijective
function
or a one-to-one correspondence.
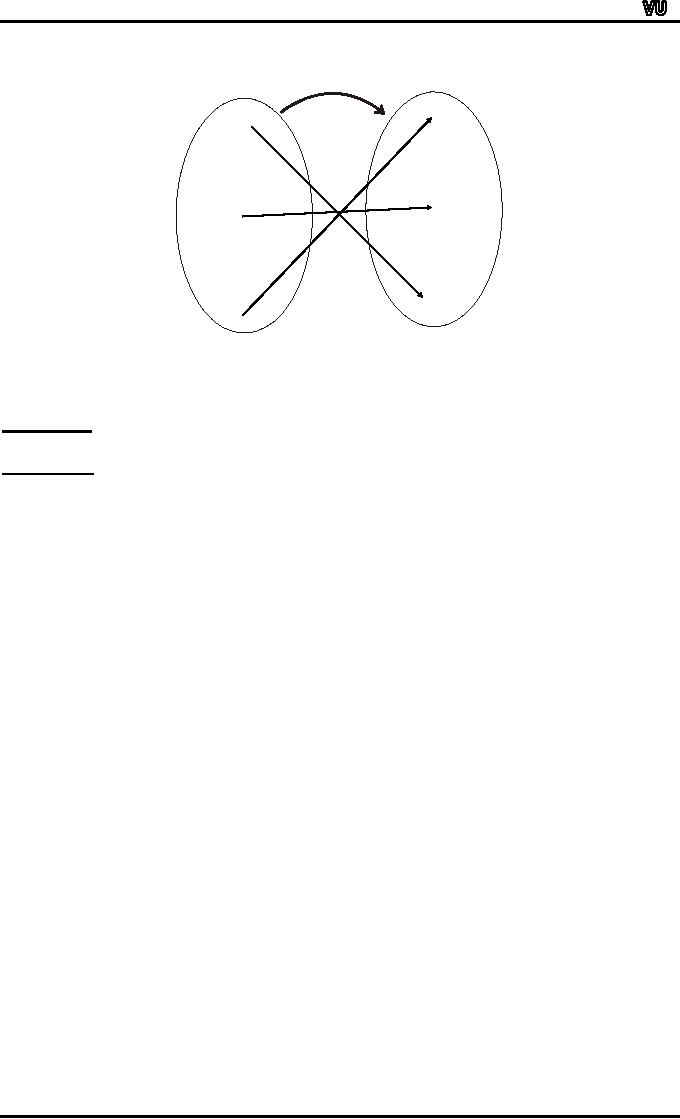
EXAMPLE:
The
function f: X→Y defined by
the arrow diagram is both
one-to-one and onto; hence
a
bijective
function.
Page
75
MTH001
Elementary Mathematics
f
1
a
2
b
.3
c
Y
X
EXERCISE:
Let
f: R →R
be defined by the rule f(x)
= x3.Show that f is a
bijective.
SOLUTION:
f
is one-to-one
x1,
x2∈R
Let
f(x1)
= f(x2)
for
x13 =
x23
⇒
x13 -
x23 = 0
⇒
(x1 -x2) (x12 +
x1x2 + x22) =
0
⇒
x12
+ x1x2 +
x22=0
⇒
x1 -
x2 = 0
or
⇒
x1
= x2
(the
second equation gives no
real solution)
Accordingly
f is one-to-one.
f
is onto
Let
y ∈R.
We search for a x ∈R such
that
f(x)=y
x3
= y
⇒
(by
definition of f)
x
= (y)1/3
or
Hence
for y ∈R, there
exists x = (y)1/3 ∈
R
such that
f(x)
= f((y)1/3)
=
((y)1/3)3 = y
Accordingly
f is onto.
Thus,
f is a bijective.
GRAPH
OF BIJECTIVE FUNCTION:
A
graph of a function f is bijective
iff every horizontal line
intersects the graph at
exactly one
point.
Page
76
MTH001
Elementary Mathematics
y
y=x3
(0,5)
O(0,0)
(5,0)
x
0
BIJEC
TIVE FUNC TION
BIJEC
TIVE FUNC TION
from
R to R
from
R to R
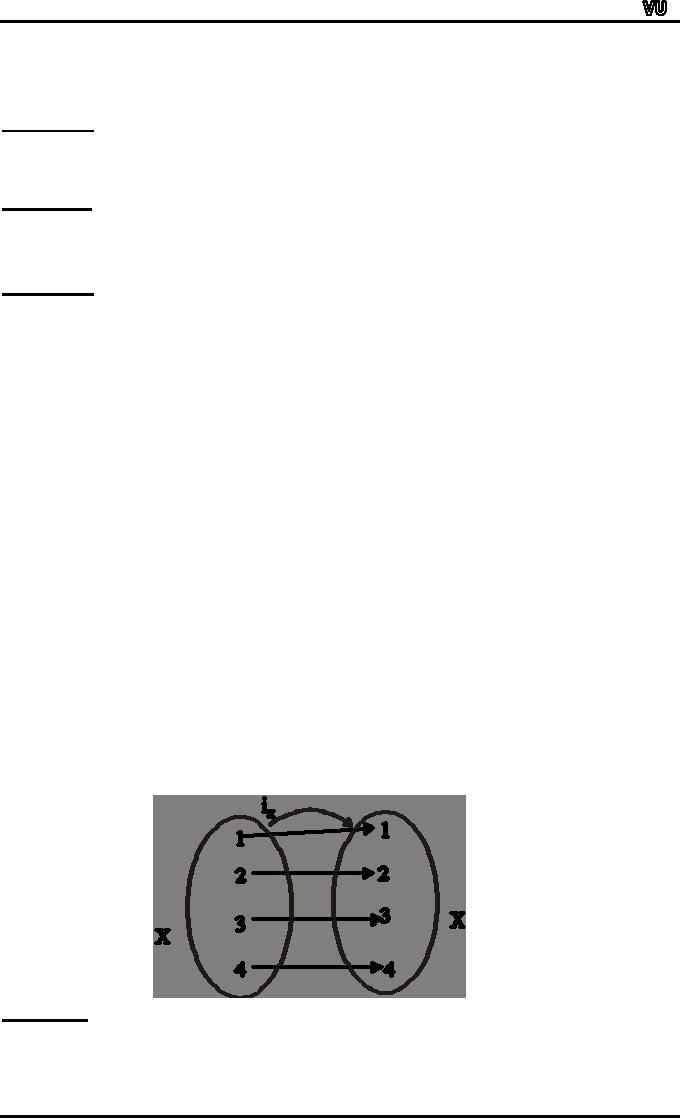
IDENTITY
FUNCTION ON A SET:
Given
a set X, define a function ix
from X to X by ix(x) = x from
all x ∈X.
The
function ix is called the
identity function on X because it
sends each element of X
to
itself.
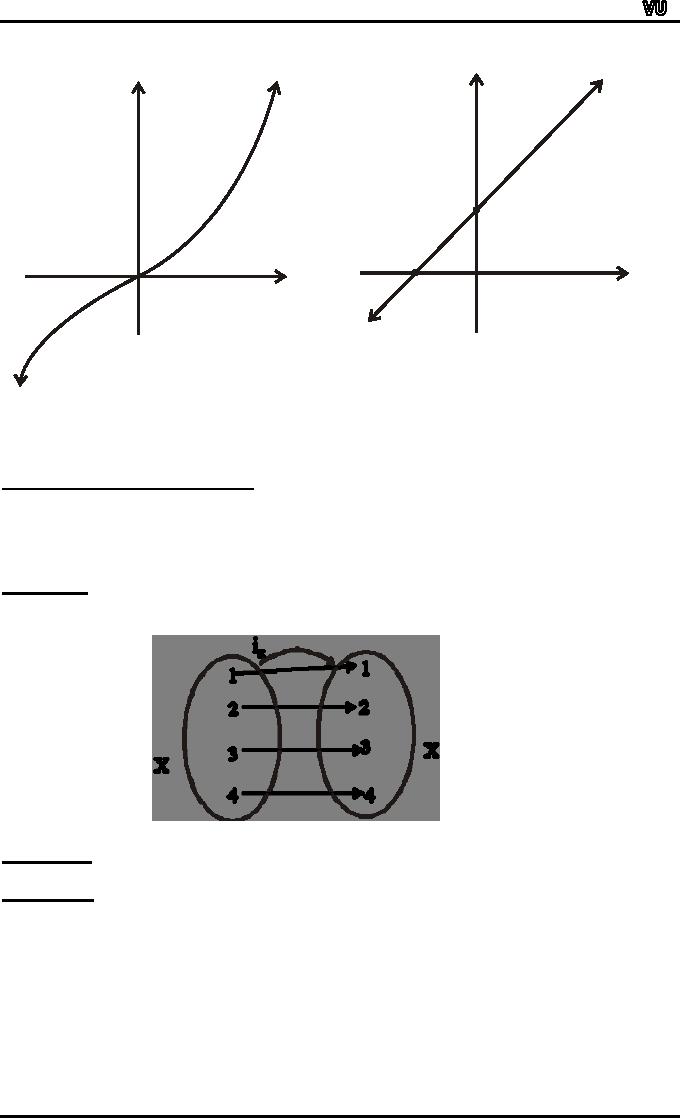
EXAMPLE:
Let
X = {1,2,3,4}. The identity
function ix on X is represented by the
arrow diagram
EXERCISE:
Let
X be a non-empty set. Prove
that the identity function
on X is bijective.
SOLUTION:
Let
ix: X →X be the
identity function defined as
ix(x) = x ∀∈X
1.
ix
is injective (one-to-one)
for
x1, x2 ∈X
Let
ix(x1) = ix(x2)
⇒
x1 =
x2
(by
definition of ix)
Hence
ix is one-to-one.
2.
ix
is surjective (onto)
Page
77

MTH001
Elementary Mathematics
Let
y ∈X
(co-domain of ix) Then there
exists y ∈X (domain of
ix) such that ix (y) =
y
Hence
ix is onto. Thus, ix being
injective and surjective is
bijective.
CONSTANT
FUNCTION:
A
function f:X→Y is a constant
function if it maps (sends)
all elements of X to one
element of
Y
i.e. ∀
x ∈X,
f(x) = c, for some c ∈
Y
EXAMPLE:
The
function f defined by the
arrow diagram is
constant.
f
Y
X
1
.7
2
.8
3
4
.9
REMARK:
1.
A constant function is one-to-one
iff its domain is a
singleton.
2.
A constant function is onto
iff its co-domain is a
singleton.
Page
78
Table of Contents:
- Recommended Books:Set of Integers, SYMBOLIC REPRESENTATION
- Truth Tables for:DE MORGAN’S LAWS, TAUTOLOGY
- APPLYING LAWS OF LOGIC:TRANSLATING ENGLISH SENTENCES TO SYMBOLS
- BICONDITIONAL:LOGICAL EQUIVALENCE INVOLVING BICONDITIONAL
- BICONDITIONAL:ARGUMENT, VALID AND INVALID ARGUMENT
- BICONDITIONAL:TABULAR FORM, SUBSET, EQUAL SETS
- BICONDITIONAL:UNION, VENN DIAGRAM FOR UNION
- ORDERED PAIR:BINARY RELATION, BINARY RELATION
- REFLEXIVE RELATION:SYMMETRIC RELATION, TRANSITIVE RELATION
- REFLEXIVE RELATION:IRREFLEXIVE RELATION, ANTISYMMETRIC RELATION
- RELATIONS AND FUNCTIONS:FUNCTIONS AND NONFUNCTIONS
- INJECTIVE FUNCTION or ONE-TO-ONE FUNCTION:FUNCTION NOT ONTO
- SEQUENCE:ARITHMETIC SEQUENCE, GEOMETRIC SEQUENCE:
- SERIES:SUMMATION NOTATION, COMPUTING SUMMATIONS:
- Applications of Basic Mathematics Part 1:BASIC ARITHMETIC OPERATIONS
- Applications of Basic Mathematics Part 4:PERCENTAGE CHANGE
- Applications of Basic Mathematics Part 5:DECREASE IN RATE
- Applications of Basic Mathematics:NOTATIONS, ACCUMULATED VALUE
- Matrix and its dimension Types of matrix:TYPICAL APPLICATIONS
- MATRICES:Matrix Representation, ADDITION AND SUBTRACTION OF MATRICES
- RATIO AND PROPORTION MERCHANDISING:Punch recipe, PROPORTION
- WHAT IS STATISTICS?:CHARACTERISTICS OF THE SCIENCE OF STATISTICS
- WHAT IS STATISTICS?:COMPONENT BAR CHAR, MULTIPLE BAR CHART
- WHAT IS STATISTICS?:DESIRABLE PROPERTIES OF THE MODE, THE ARITHMETIC MEAN
- Median in Case of a Frequency Distribution of a Continuous Variable
- GEOMETRIC MEAN:HARMONIC MEAN, MID-QUARTILE RANGE
- GEOMETRIC MEAN:Number of Pupils, QUARTILE DEVIATION:
- GEOMETRIC MEAN:MEAN DEVIATION FOR GROUPED DATA
- COUNTING RULES:RULE OF PERMUTATION, RULE OF COMBINATION
- Definitions of Probability:MUTUALLY EXCLUSIVE EVENTS, Venn Diagram
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:ADDITION LAW
- THE RELATIVE FREQUENCY DEFINITION OF PROBABILITY:INDEPENDENT EVENTS