 |
Limits (Intuitive Introduction) |
| << Graphs of Functions |
| Limits and Computational Approach >> |
Calculus
and Analytical
Geometry
MTH101
LECTUER
9
Limits
(Intuitive Introduction)
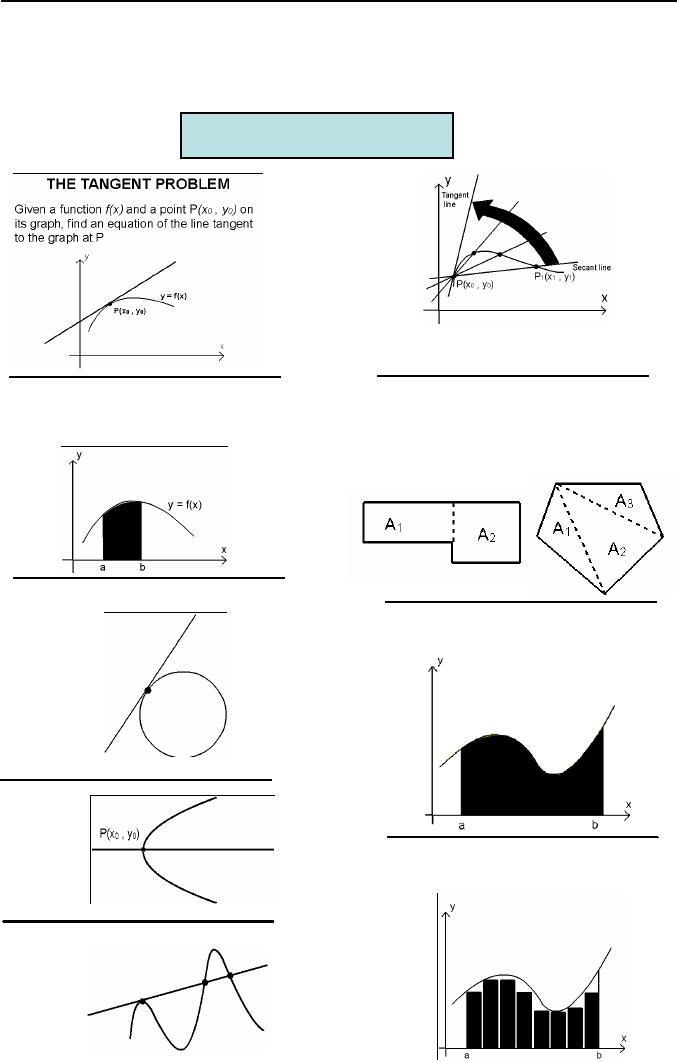
The
line occupying this limiting
position
we
consider to be tangent line at
P.
THE
AREA PROBLEM
The
areas of some plane regions
can
be
calculated by subdividing them
into
Given
a function f, find the area
between
finite
number of rectangles or
triangle,
the
graph of the f and an
interval [a,b] on the
then
adding the area of the
constituent
x-axis
parts.
A
line is called
tangent
For
many regions a more general
approach
to
a circle if
is
needed.
it
meets
the
circle
at
precise
ly
one
point.
But
this
definition
is
not satis-
factory
for
We
approximate the area of this
region by
other
kind
inscribing
rectangles of equal width
under
of
curves, like
The
curve and adding the
areas of these
rectangles.
The
line is
tangent
yet it
meets
the
curve
more
than
once.
Mth101
Page
24
Calculus
and Analytical
Geometry
Limits
(Intuitive Introduction)
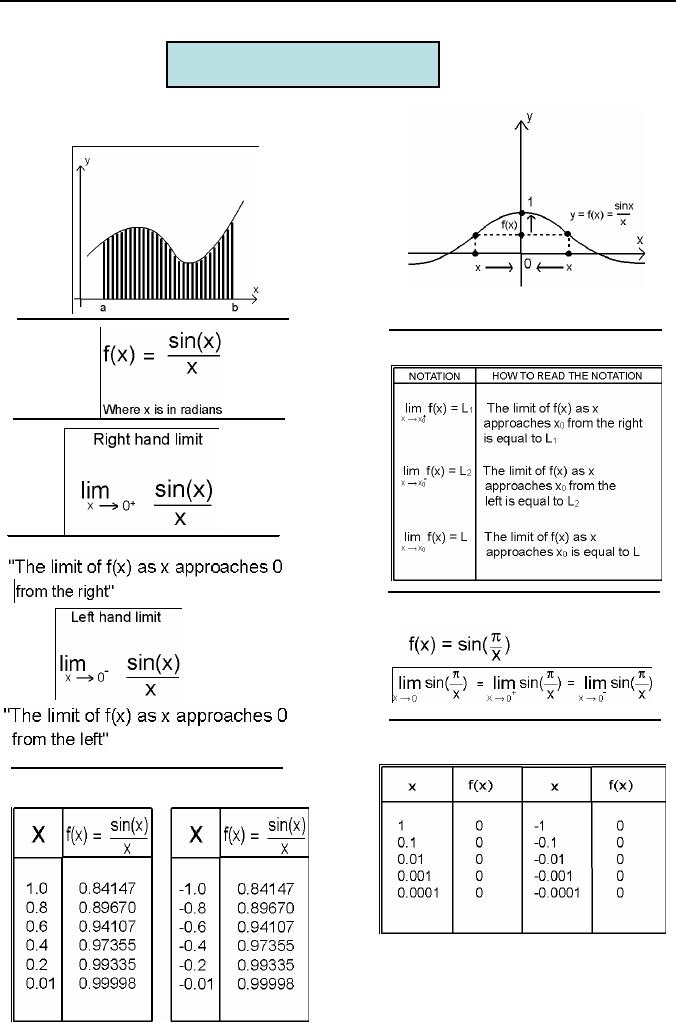
Our
approximations will "approach"
the
exact
area under the curve as a
"limiting
value".
As
x approach 0 from the
left
or
right, f(x) approach
1.
Let
us take
The
preceding ideas are
summarized in this
table.
Numerical
Pitfalls
Table
2.4.4
Using
a calculator set to the
radian mode, we have
Mth101
Page
25
Calculus
and Analytical
Geometry
Limits
(Intuitive Introduction)
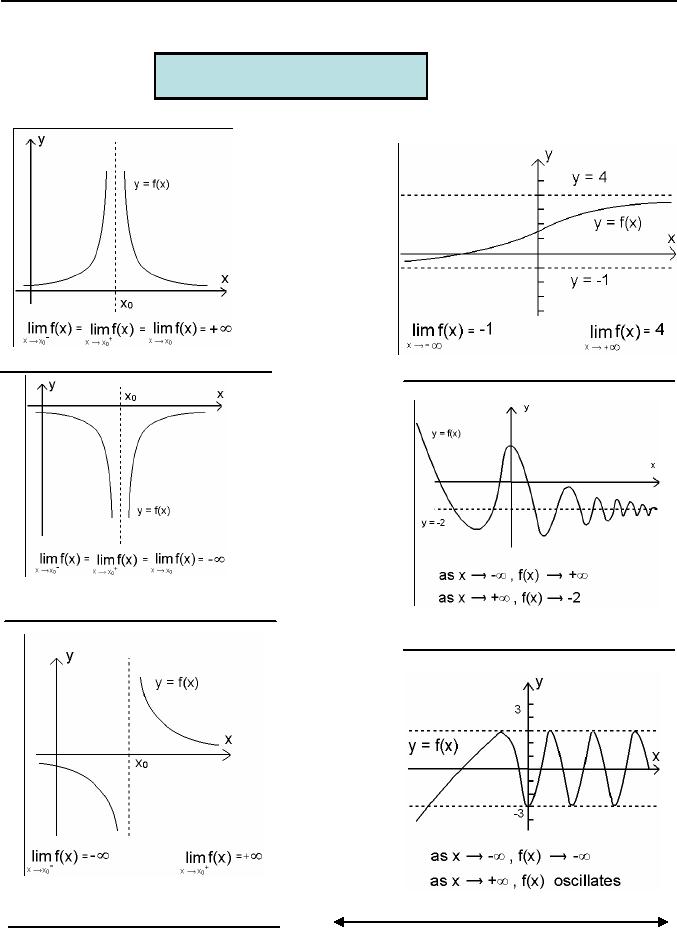
Existence
of limits
Example
Here
x
approaches X0 from
left
So,
limit of function does not
exist.
Example
Here
x
approaches X0 from
right
So,
limit of function does not
exist.
Example
Example
Here
The
limit of the function does
not exist at X0
So,
limit of function does not
exist.
Mth101
Page
26
Table of Contents:
- Coordinates, Graphs and Lines
- Absolute Values
- Coordinate Planes and Graphs
- Line and Definition of Slope
- Distance, Circles, Quadratic Equations
- Functions and Limits
- Operations on Functions
- Graphs of Functions
- Limits (Intuitive Introduction)
- Limits and Computational Approach
- Limits: A Rigorous Approach
- Continuity
- Limit and Continuity of Trigonometric Functions
- Tangent Lines and Rates of Change
- The Derivative