ZeePedia

Distance, Circles, Quadratic Equations

<< Line and Definition of Slope

Functions and Limits >>

Calculus and Analytical Geometry

MTH101

LECTUER 5

Distance, Circles, Quadratic Equations

In this lecture we shall discuss:

Exampl

Since we know that if A and B are points

e

on a coordinate line with coordinate a and

b,

respectively, then the distance between A

and B is

Since

So

If x, y and z are base, perpendicular and

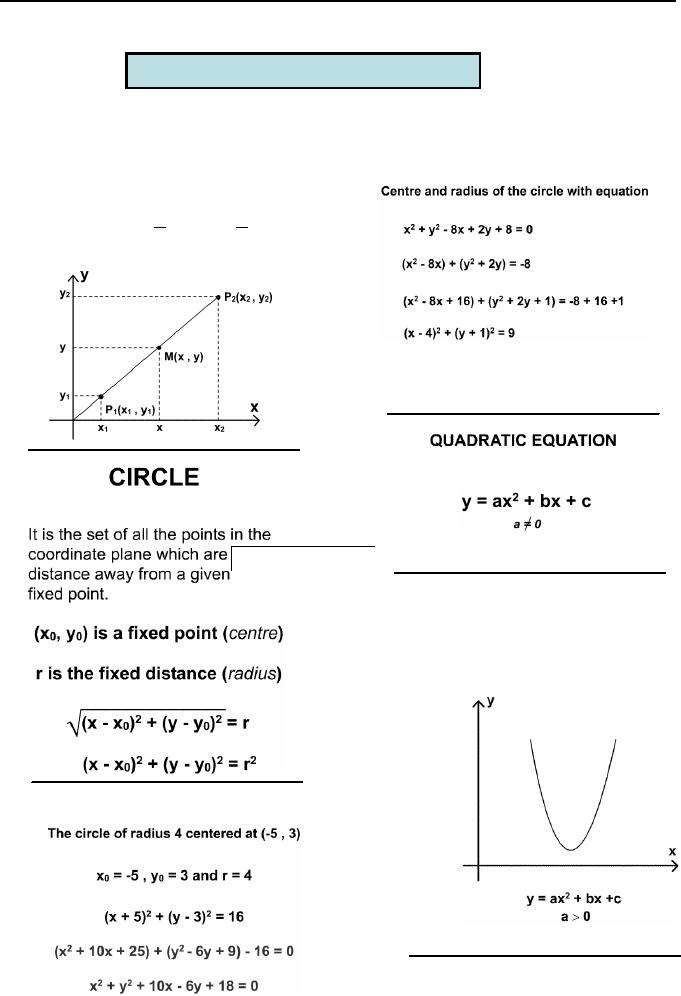
The Midpoint Formula

hypotenuse of a right triangle respectively,

then

To derive the midpoint formula, we shall

start with two points on a coordinate line.

In the following figure, the distance between

a and b, and their midpoint is shown.

So, the midpoint is

Now from above figure, the length of the

horizontal side is [x2 - x1 ] and the length

of the vertical side is [y2 - y1 ] , so it

follows

from the Theorem of Pythagoras that

Since

So

Mth101

Page 14

Calculus and Analytical Geometry

Distance, Circles, Quadratic Equations

Finding the Center and Radius

Theorem:

of a Circle

The midpoint of the line segment joining

two points (x1 , y1 ) and (x2 , y2 ) in a

Example:

coordinate plane is

⎛1

⎞

1

midpo int = ( x, y ) = ⎜ ( x1 + x2 ) , ( y1 + y2 ) ⎟

⎝2

2

⎠

So comparing with general equation of

circle we find that center=(4,-1) and

radius = 3

An equation of the form

is called a quadratic equation.

at a fixed

The graph of y = ax2 + bx+c

Let

The vertex is the low point on the curve

And

if a>0, as shown.

Then

Example:

Mth101

Page 15

Calculus and Analytical Geometry

Distance, Circles, Quadratic Equations

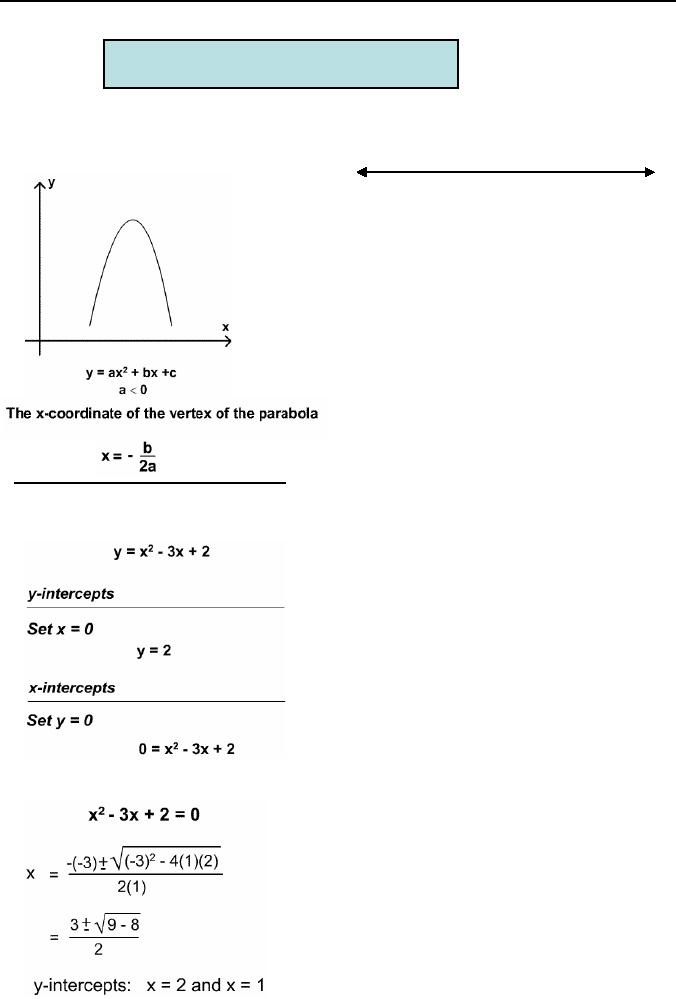
The vertex is the high point on the curve

if a<0, as shown.

Example

:

Sketch the graph of

Thus by using quadratic formula, we have

Mth101

Page 16

Table of Contents: