 |
Line and Definition of Slope |
| << Coordinate Planes and Graphs |
| Distance, Circles, Quadratic Equations >> |
Calculus
and Analytical
Geometry
MTH101
LECTUER
4
Line
and Definition of
Slope
horizontally
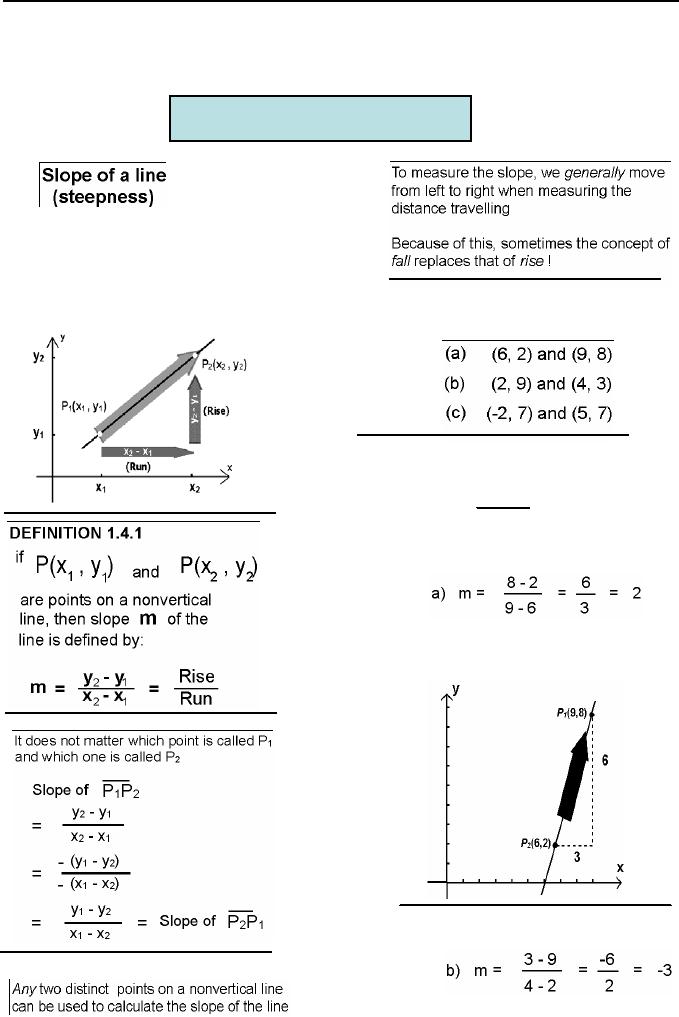
Consider
a particle moving along
a
non
vertical line segment from a
point
p1( x1,y1 )
to a point p1(
x1,y1 ) .
The
vertical change y2
y1 is called
the
rise, and the horizontal
change
Example:
In each
part find the slope
of
x2
x1the run.
the
line through
Solution:
We
know that slope of line
through two points
p1( x1,y1
) and
p1( x1,y1
) , is given
by
m=
y2 y1
x2
x1
So
On
coordinate plane xy
Similarly
Mth101
Page
11
Calculus
and Analytical
Geometry
Line
and Definition of
Slope
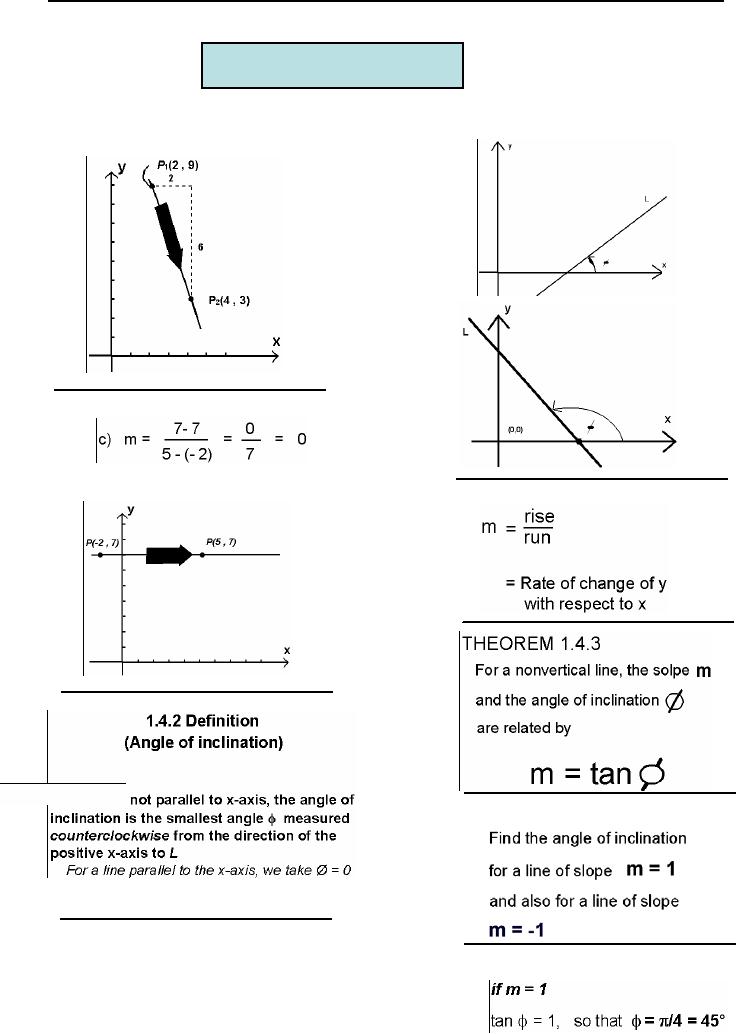
On
coordinate plane xy
Also
On
coordinate plane xy
If
m is slope of line
then,
For
a
line
L is
Example:
As
shown in the following
figures.
Solution:
Mth101
Page
12
Calculus
and Analytical
Geometry
Line
and Definition of
Slope
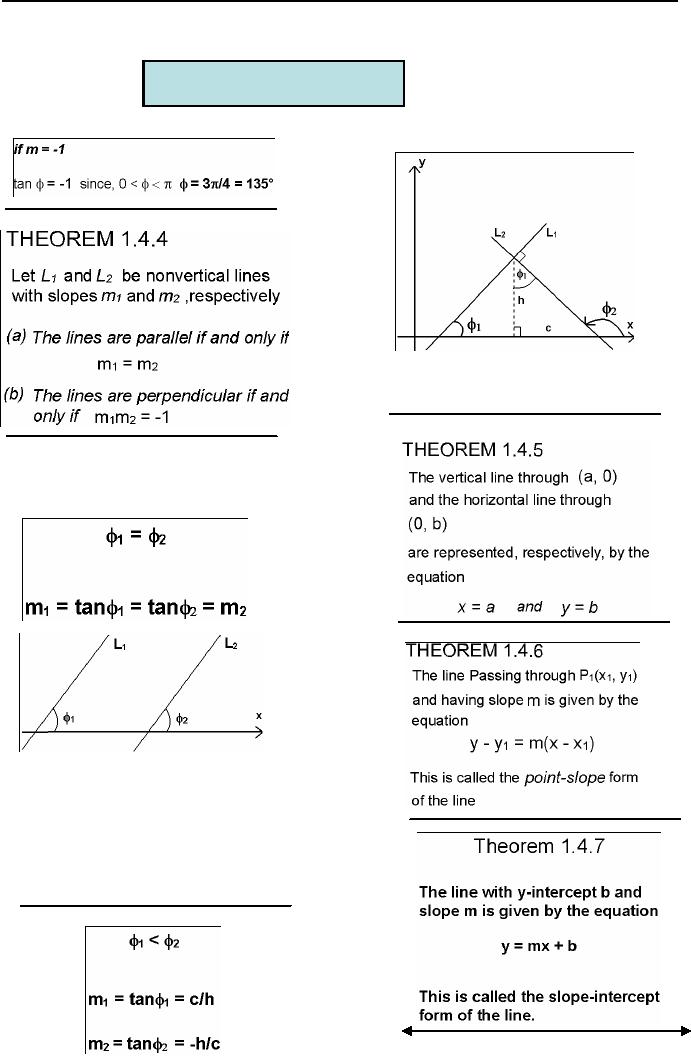
The
proof of the converse is
left as an
exercise.
Proof:
(a)
If
L1 and L2
are
non vertical lines, then
their
angles
of inclination �1 and
�2 are
equal.
Thus
Conversely,
if two slope lines are
equal, I.e.
M1
= M2
⇒
tan(�1)=tan(�2)
⇒
�1
= �2
So,
lines are parallel.
(b)
Assume that
Then
referring to the
figure
Mth101
Page
13
Table of Contents:
- Coordinates, Graphs and Lines
- Absolute Values
- Coordinate Planes and Graphs
- Line and Definition of Slope
- Distance, Circles, Quadratic Equations
- Functions and Limits
- Operations on Functions
- Graphs of Functions
- Limits (Intuitive Introduction)
- Limits and Computational Approach
- Limits: A Rigorous Approach
- Continuity
- Limit and Continuity of Trigonometric Functions
- Tangent Lines and Rates of Change
- The Derivative