ZeePedia

Coordinate Planes and Graphs

<< Absolute Values

Line and Definition of Slope >>

Calculus and Analytical Geometry

MTH101

LECTUER 3

Coordinate Planes and Graphs

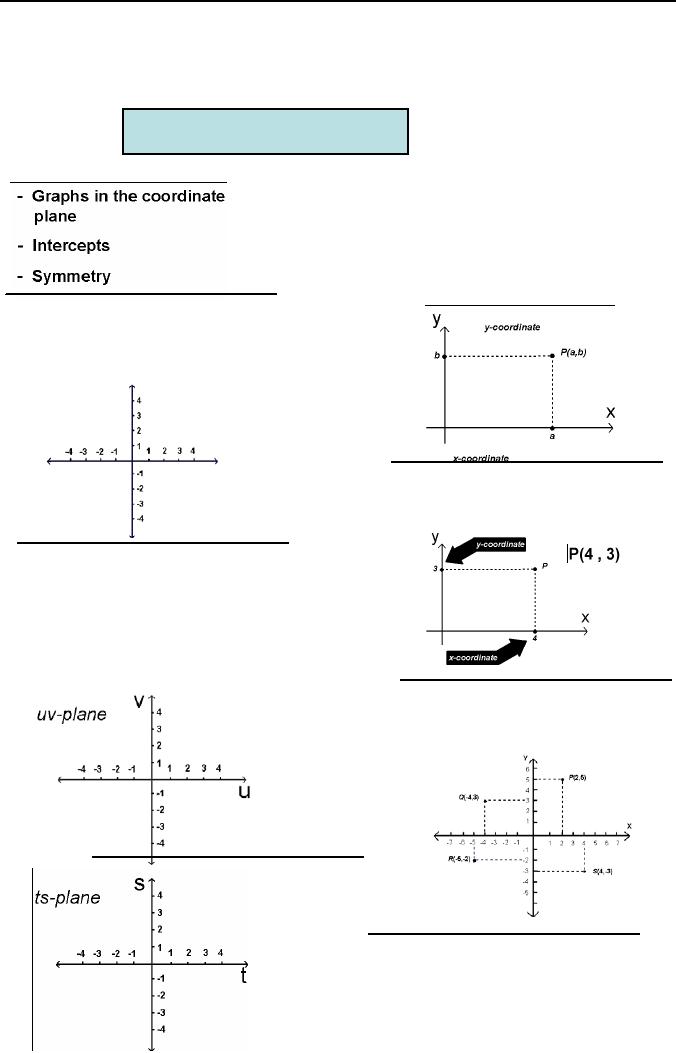
Ordered pair

In this lecture we shall discuss:

By an ordered pair of real numbers we

mean two real numbers in an assigned

order. Every point P in a coordinate plane

can be associated with a unique ordered

pair of real numbers by drawing two lines

through P, one perpendicular to the x-axis

and the other to the y-axis.

A rectangular coordinate system is

a pair of perpendicular coordinate lines,

called coordinate axes, which are placed

So that they intersect at their origins.

For example if we take (a,b)=(4,3), then

on coordinate plane

The labeling of axes with letters x and y

is a common convention, but any letters may

be used. If the letter x and y are used to label

the coordinate axes, then the resulting plane

is called xy-plane. In applications it is common

to use letters other than x and y is shown In

the following figures, as uv-plane and ts-plane.

To plot a point P(a,b) means to locate

the point with coordinates (a,b) in a coordinate

plane. For example, different points are plotted.

In a rectangular coordinate system the

coordinate axes divide the plane into four

regions called quadrants. These are

numbered counterclockwise with roman

numerals as shown

Mth101

Page 7

Calculus and Analytical Geometry

Coordinate Planes and Graphs

This is an approximation to the graph of

Y=x2

. N general, it is only with techniques

from calculus that the true shape of a graph

Ca can be ascertained.

Consider the equations

We define a solution of such an equation

to be an ordered pair of

real numbers(a,b) so that the equation

is satisfactory when we substitute x=a and y=b.

Example

Sketch the graph of

Exampl

:

e

Because 1/x is undefined when x=0,

Example: Sketch the graph of

we

can plot only points for which x=0

Mth101

Page 8

Calculus and Analytical Geometry

Coordinate Planes and Graphs

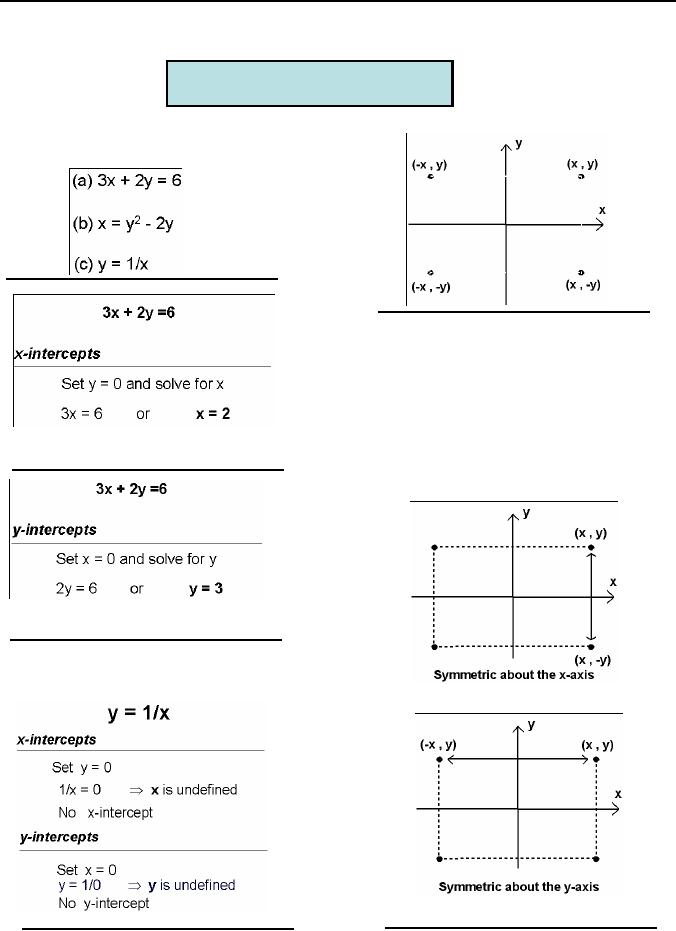
Example:

Find all intercepts of

Solution:

· symmetric about the x-axis if for each

point (x,y) on the graph the point (x,-y)

is also on the graph.

· symmetric about the y-axis if for each

point (x,y) on the graph the point (-x,y)

is also on the graph.

· symmetric about the origin, if for

is the required x-intercept.

each point (x,y) on the graph the point

(-x,-y) is also on the graph.

is the required y-intercept.

Similarly you can solve part (b), the

part (c) is solved here

In the following figure, the points (x,y),

(-x,y),(x,-y) and (-x,-y) form the corners

of a rectangle.

Mth101

Page 9

Calculus and Analytical Geometry

Coordinate Planes and Graphs

Example:

yields

Example:

Mth101

Page 10

Table of Contents: