 |
Tangent Lines and Rates of Change |
| << Limit and Continuity of Trigonometric Functions |
| The Derivative >> |
Calculus
and Analytical
Geometry
MTH101
LECTUER
14
Tangent
Lines and Rates
of
Change
Slope
of a Tangent Line
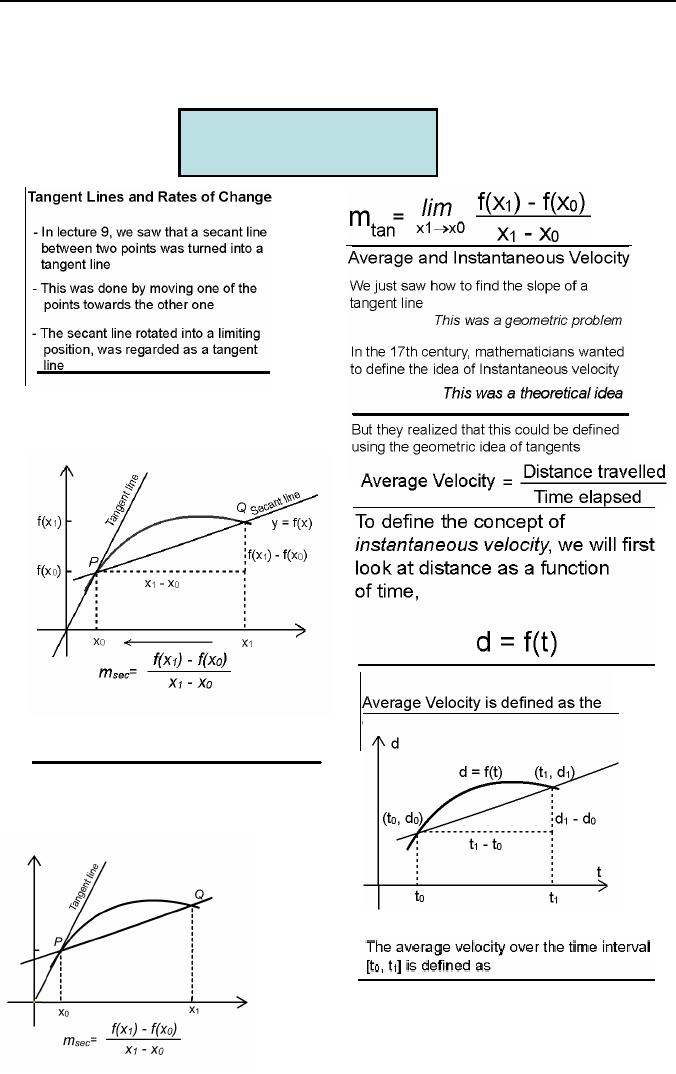
If
a secant line is drawn
between
two
points P and Q on a curve,
then
the
slope of this secant line
is
If
we let X1 approach
XD , then Q will
approach
P along the graph of f, and
the
secant
line through P and Q will
approach
the
tangent line at P. Thus
slope of secant
approaches
the slope of tangent.
Mth101
Page
43
Calculus
and Analytical
Geometry
Tangent
Lines and Rates
of
Change
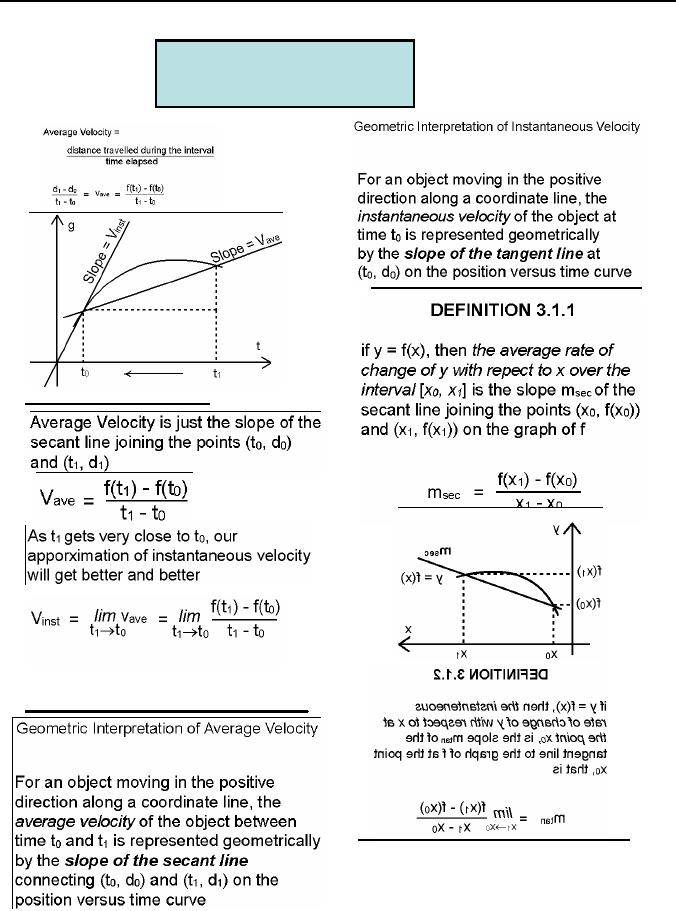
This
shows that secant line
approaches to
tangent
line. Thus we can conclude
that the
slope
of this tangent line is the
instantaneous
velocity.
Mth101
Page
44
Calculus
and Analytical
Geometry
Tangent
Lines and Rates
of
Change
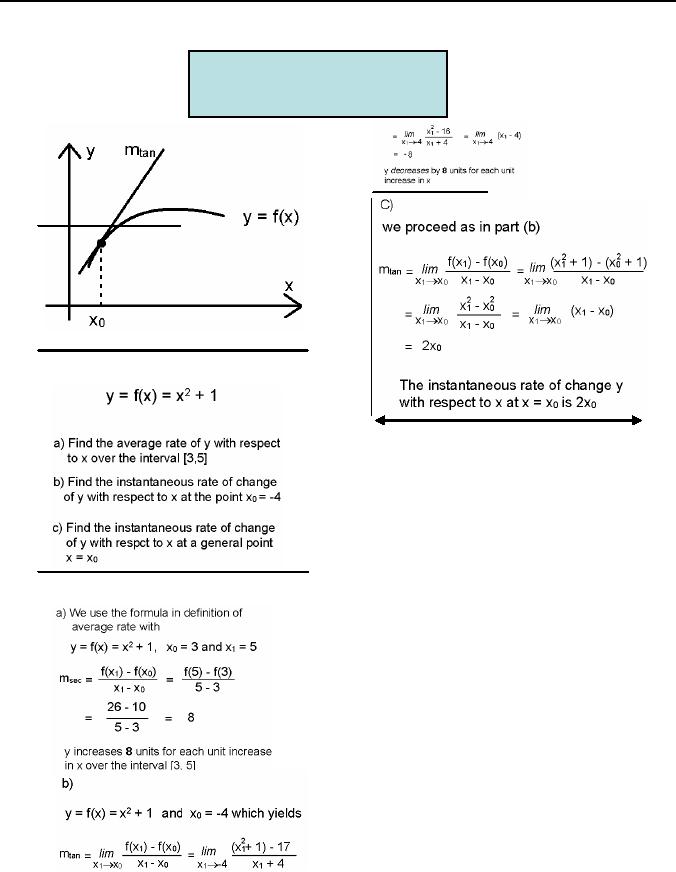
Example
Solution
Mth101
Page
45
Table of Contents:
- Coordinates, Graphs and Lines
- Absolute Values
- Coordinate Planes and Graphs
- Line and Definition of Slope
- Distance, Circles, Quadratic Equations
- Functions and Limits
- Operations on Functions
- Graphs of Functions
- Limits (Intuitive Introduction)
- Limits and Computational Approach
- Limits: A Rigorous Approach
- Continuity
- Limit and Continuity of Trigonometric Functions
- Tangent Lines and Rates of Change
- The Derivative