ZeePedia

Limit and Continuity of Trigonometric Functions

<< Continuity

Tangent Lines and Rates of Change >>

Calculus and Analytical Geometry

MTH101

LECTUER 13

Limit and Continuity of

Trigonometric Functions

B(1,0)

It is evident that as h approaches 0, the

coordinate of P approach the corresponding

coordinate of B.

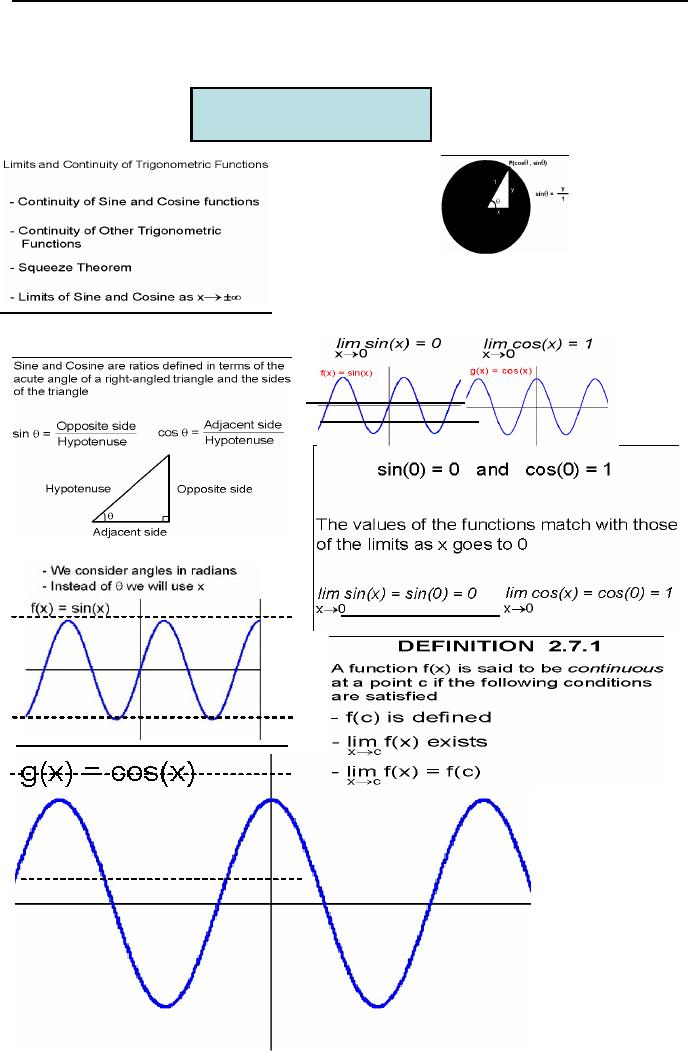
Continuity of Sine and Cosine

function

But by definition we know

Here is the graph of Sinx and Cosx

Remind the definition of continuity we have

1

Hence we have the following theorem

0

-1

1

0

-1

Mth101

Page 38

Calculus and Analytical Geometry

Limit and Continuity of

Trigonometric Functions

Proof

Similarly, since

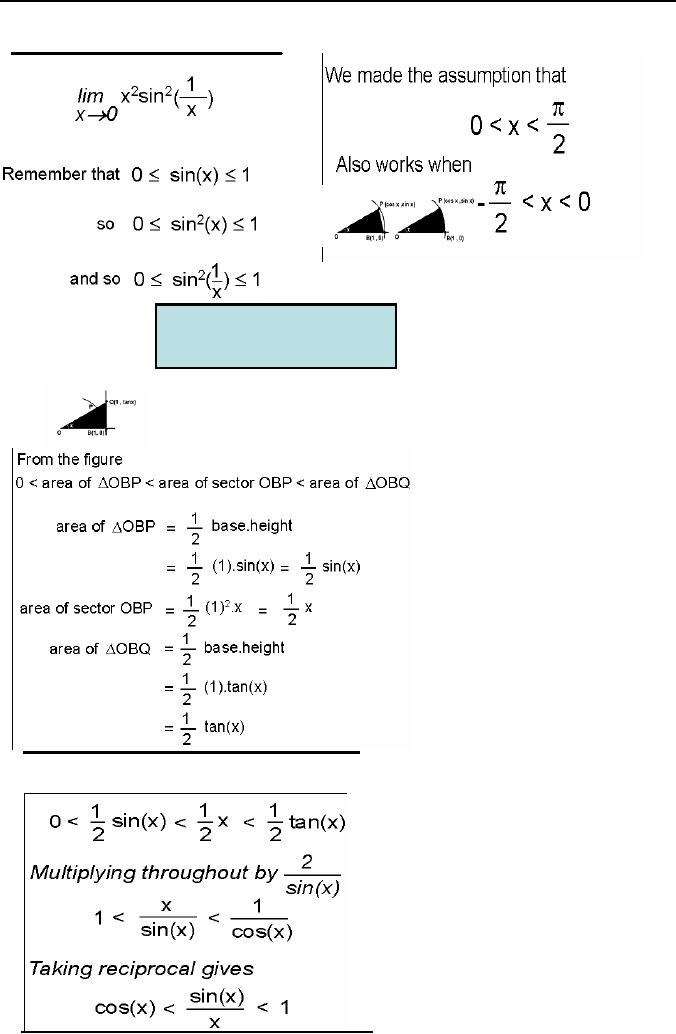
Obtaining Limits by Squeezing

Mth101

Page 39

Calculus and Analytical Geometry

Now

Consider the graph of

o

Hence proved.

And

Limit and Continuity of

Trigonometric Functions

And the graph of

o

Here the problem is:

Before proving next theorem, let us see

the following formula.

Here we cannot write these functions

in some other form by using algebraic

Manipulation to solve this problem. So here

we will use some other method. One such

method is to obtain by following theorem;

Mth101

Page 40

Calculus and Analytical Geometry

Example: Use the squeezing theorem

to evaluate

Solution

Limit and Continuity of

Trigonometric Functions

So, the above inequality becomes

Mth101

Page 41

Calculus and Analytical Geometry

Mth101

Page 42

Table of Contents: