 |
Limits and Computational Approach |
| << Limits (Intuitive Introduction) |
| Limits: A Rigorous Approach >> |

Calculus
and Analytical
Geometry
MTH101
LECTUER
10
Limits
and Computational
Approach
Some
basic limit for
Table
2.5.1
(a)
(b)
Now
for
(c)
Mth101
Page
27

Calculus
and Analytical
Geometry
Limits
and Computational
Approach
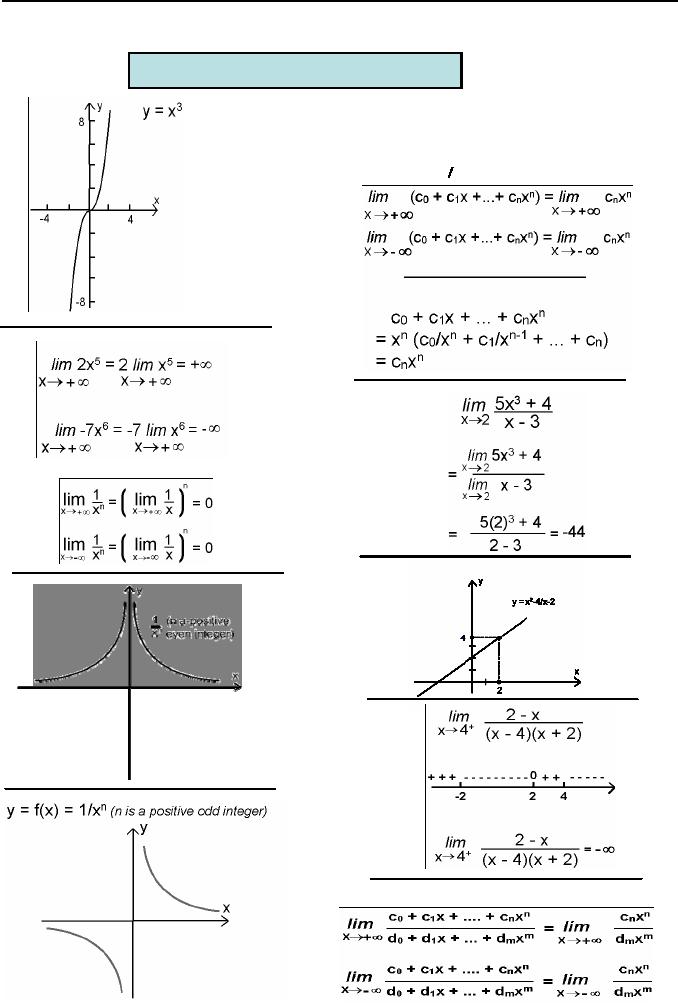
Theorem
If
f1,f2 ,...........,fn are
same functions
Thus
we can write
Another
useful result
Where
k is constant
A
polynomial is an expression of the
form
Where
bn ,
bn
1,,.... ,
b1 , b0
are
all constants.
Remark
Although
the results ( a ) and ( c )
are
Example
stated
for two functions f and g,
these
Results
hold as well for and
finite number
of
functions; that is, if the
limits lim f1 (x),
Lim
f2 ( x
),..........lim fn ( x )
all exists,
then
and
Mth101
Page
28

Calculus
and Analytical
Geometry
Limits
and Computational
Approach
Proof:
Limit
involving
1
x
The
following limits are
suggested by
the
graph of 1/x.
Table
of numerical values
For
every real number a the
graph of
the
function
Lim
x2 =
+00
Lim
x = +00
x→+00
x→+00
Lim
x2 =
+00
Lim
x = +00
x→+00
x→+00
Mth101
Page
29
Calculus
and Analytical
Geometry
Limits
and Computational
Approach
A
polynomial behaves like its
term of highest
degree
as x→+00
or
x→-00
more
precisely,
if cn =
0
,
then
Lim
x3 =
+00
x→+00
Lim
x3 =
-00
Thus
x→+00
Example
Example
For
integer value of n
The
graph has not value at x =
2
Example
Quick
method for finding limit of
rational functions
Mth101
Page
30
Table of Contents:
- Coordinates, Graphs and Lines
- Absolute Values
- Coordinate Planes and Graphs
- Line and Definition of Slope
- Distance, Circles, Quadratic Equations
- Functions and Limits
- Operations on Functions
- Graphs of Functions
- Limits (Intuitive Introduction)
- Limits and Computational Approach
- Limits: A Rigorous Approach
- Continuity
- Limit and Continuity of Trigonometric Functions
- Tangent Lines and Rates of Change
- The Derivative